zkw线段树——简单易懂好写好调的线段树
0.简介
zkw线段树是一种非递归线段树,与普通线段树不同的是,它是棵标准的满二叉树,所以遍历过程可全程使用位运算,常数一般比线段树小得多。
1.结构/建树
前面说了,zkw线段树是满二叉树,可是原数组大小不一定是2^n,所以我们就多开一些废点,硬充,另外,它需要左右各两个点当哨兵,原因看下面的查询原理就知道了。
有人会想,开一些废点是不是空间会更大,相反,一般线段树由于相比之下结构混乱,一般开4倍,而zkw只用开3倍。
这就是zkw:

在zkw线段树中,最下面一排的点就是原数组上的点,因为是满二叉树,所以这些点的深度都一样,设为d(1的深度为0,图中d为4),然后会发现底排上面的点(从1~15)数量刚好为2^d-1,原数组中的元素编号(最底下红色字体)对应的线段树上的点的编号恰好增加了2^d,最低排点数也为2^d(包括废点),那么我们只需要知道这个常数d,就可以确定这棵树的结构了,所以建树很简单,只需要计算最小的、使最低排点数足够的d,实际上,计算2^d后面更方便:
int M; //M 即 2^d
void maketree(int n) {//原数组长度
M = 1; while(M < n+2/*包括哨兵*/) M <<= 1;
}2.单点修改
我们知道了2^d,就可以直接求出原数组中某个元素在线段树上的点,然后一路向上更新(编号/2下取整即为其父亲的编号):
void addtree(int x,int y) {//y的类型视情况而变
int s = M + x;
tre[s] = y; s >>= 1;
while(s) {
tre[s] = Merge(tre[s<<1],tre[s<<1|1]);//自定义的某种合并操作,可以是相加、相乘、最大值最小值等
s >>= 1;
}
}3.区间查询
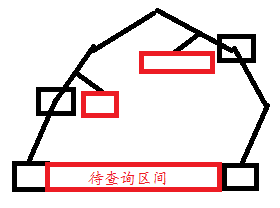
当我们知道要查询的区间[l,r]时,就把区间两端往外的两个点记录为s(M+(l-1)),t(M+(r+1)),那么两点到 lca 路径包围住的点就恰好是要查询的区间,把s和t往父亲方向走,每当s为其父亲的左儿子(s为偶数),那它的兄弟一定在区间里(s ^ 1),每当t为其父亲的右儿子(t为奇数),那它的兄弟也一定在区间里(t ^ 1):
int findtree(int l,int r) {
int s = M + l - 1,t = M + r + 1;
int ans = 0;
while(s || t) {
if((s>>1) ^ (t>>1)) { // s/2 != t/2
if(!(s & 1)) ans = Merge(ans,tre[s ^ 1]);
if(t & 1) ans = Merge(ans,tre[t ^ 1]);
}
else break;
s >>= 1;t >>= 1;
}
return ans;
}
4.永久化懒标记
zkw线段树的修改和查询都是从下往上做,因此懒标记不方便往下放,于是就用永久化的懒标记,记录整个子树的修改(不包括子树的根),以后每次查询都要按照深度依次修改答案。
用懒标记就可以支持不按时间顺序修改的区间修改了,和不用懒标记的区间查询差不多,但是要修改访问到的区间内点的懒标记,并且更新经过的所有节点,也就是说不能中途break了。
以区间最大值为例:
void addtree(int l,int r,int y) { //区间修改
int s = M + l - 1,r = M + r + 1;
while(s || t) {
if(s < M) tre[s] = max(tre[s<<1],tre[s<<1|1]) + lz[s]; //lz[]为懒标记数组
if(t < M) tre[t] = max(tre[t<<1],tre[t<<1|1]) + lz[t]; //路途中的节点修改,但不包括最下面一排,因为它们没有子节点
if((s>>1) ^ (t>>1)) {
if(!(s & 1)) tre[s^1] += y,lz[s^1] += y;
if(t & 1) tre[t^1] += y,lz[t^1] += y;
} //不能break
s >>= 1;t >>= 1;
}
}
void findtree(int l,int r) { //区间查询
int s = M + l - 1,r = M + r + 1;
int ls = 0,rs = 0; //左右两边单独算,因为左边每一个父亲只能照顾左边路径上的子孙,右边同理
while(s || t) {
ls += lz[s];
rs += lz[t];
if((s>>1) ^ (t>>1)) {
if(!(s & 1)) ls = max(ls,tre[s^1]); //这里不能考虑懒标记,因为懒标记省略的修改不包括自己
if(t & 1) rs = max(rs,tre[t^1]); //当然,这只是笔者个人的写法,看官随意
}
s >>= 1;t >>= 1;
}
return max(ls,rs);
}5.其他
除了这些操作,zkw还可以支持线段树二分,只不过只有到最底层的时候,才能知道具体的位置。
记录每个点的具体区间范围、长度,甚至可以将就打递归版。
此外,zkw线段树结构的性质还可以运用到其他题目上。



