Rodrigues' Rotation Formula(罗德里格旋转公式)
罗德里格旋转公式:三维空间中向量\(v\)绕单位向量\(u\)旋转\(\theta\)角度之后得到的\(\boldsymbol{v^{'}}\)
\[\bm{v^{'}}=\bm{v}cos\theta+(\bm{u}\cdot\bm{v})\bm{u}(1-cos\theta)+(\bm{u}\times\bm{v})sin\theta
\]
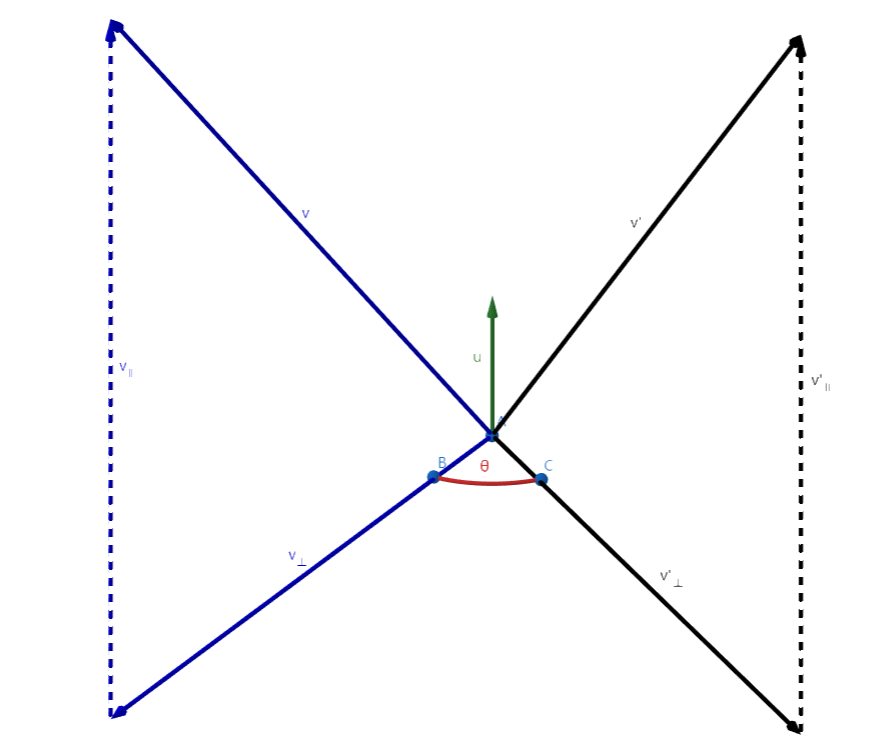
首先我们可以将\(\boldsymbol{v^{'}}\)分解为平行\(\boldsymbol{u}\)和垂直\(\boldsymbol{u}\)的两个向量,\(\boldsymbol{v_{||}}\)可以用叉积较容易求出。
\[\begin{equation}
\begin{aligned}
\boldsymbol{v_{||}}&=|\boldsymbol{v_{||}}|\boldsymbol{u} \\
&=\frac{\boldsymbol{u}\cdot\boldsymbol{v}}{|\boldsymbol{u}|}\boldsymbol{u} \\
&=(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u}
\end{aligned}
\end{equation}
\]
我们可以通过构造正交系来求得\(\boldsymbol{v_{\perp}^{'}}\),我们可以知道\(\boldsymbol{u}\times\boldsymbol{v_{\perp}}\)和\(\boldsymbol{v_{\perp}}\)是正交且模长相同且三个向量在一个平面,那么我们可以将\(\boldsymbol{v_{\perp}^{'}}\)表示出来。
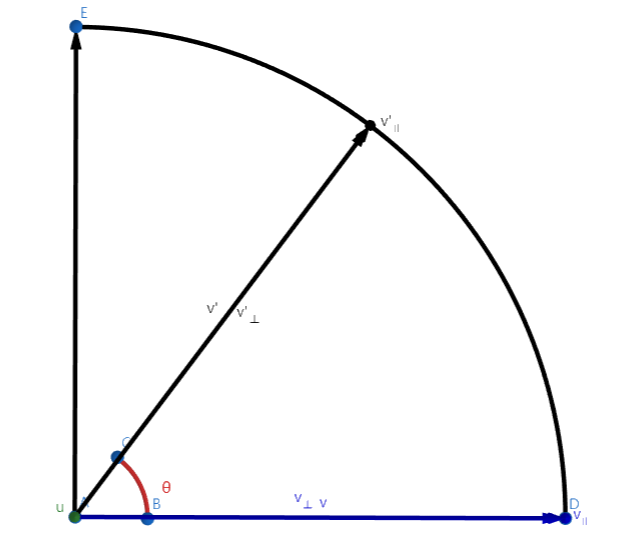
\[\begin{equation}
\begin{aligned}
\boldsymbol{v_{\perp}^{'}}&=\boldsymbol{u}\times\boldsymbol{v_{\perp}}sin\theta+\boldsymbol{v_{\perp}}cos\theta \\
&=\boldsymbol{u}\times(\boldsymbol{v}-\boldsymbol{v_{||}})sin\theta+(\boldsymbol{v}-\boldsymbol{v_{||}})cos\theta \\
&=\boldsymbol{u}\times(\boldsymbol{v}-(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u})sin\theta+(\boldsymbol{v}-(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u})cos\theta \\
&=\boldsymbol{u}\times\boldsymbol{v}sin\theta+\boldsymbol{v}cos\theta-(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u}cos\theta
\end{aligned}
\end{equation}
\]
结合\((1)(2)\)式我们可以得到\(\boldsymbol{v^{'}}\)。
\[\begin{equation}
\begin{aligned}
\boldsymbol{v^{'}}&=\boldsymbol{v_{||}^{'}}+\boldsymbol{v_{\perp}^{'}} \\
&=\boldsymbol{v_{||}}+\boldsymbol{v_{\perp}^{'}} \\
&=\boldsymbol{v}cos\theta+(\boldsymbol{u}\cdot\boldsymbol{v})\boldsymbol{u}(1-cos\theta)+(\boldsymbol{u}\times\boldsymbol{v})sin\theta
\end{aligned}
\end{equation}
\]

