POJ 3410 Split convex polygon(凸包)
题意是逆时针方向给你两个多边形,问你这两个多边形通过旋转和平移能否拼成一个凸包。
首先可以想到的便是枚举边,肯定是有一对长度相同的边贴合,那么我们就可以n2枚举所有边对,接下来就是旋转点对,那么假设多边型在这条向量的左侧,那么我们可以根据叉积正负判断旋转的方向。
然后就是如何判断了,显然有一种情况是凸包里扣除整个多边形,那么这种情况我们需要对重合的边进行删除,可以发现,如果有重合的边,他一定是成对出现,有一条进去的边也有一条出来的边,那么我们可以直接通过vector不断插入的过程和之前那条边比较,是否是同一对点产生的边,如果是我们就直接抵消,进行下一次判断。
最后就是对这些绕着一圈的点进行判断是否是凸包,那么我们直接绕一圈判断两个向量叉积是否是小于0或者叉积等于0但是方向相反,那么这种情况也是非法。
还是有很多细节地方,此题好像eps要开大一点,不然会wa。
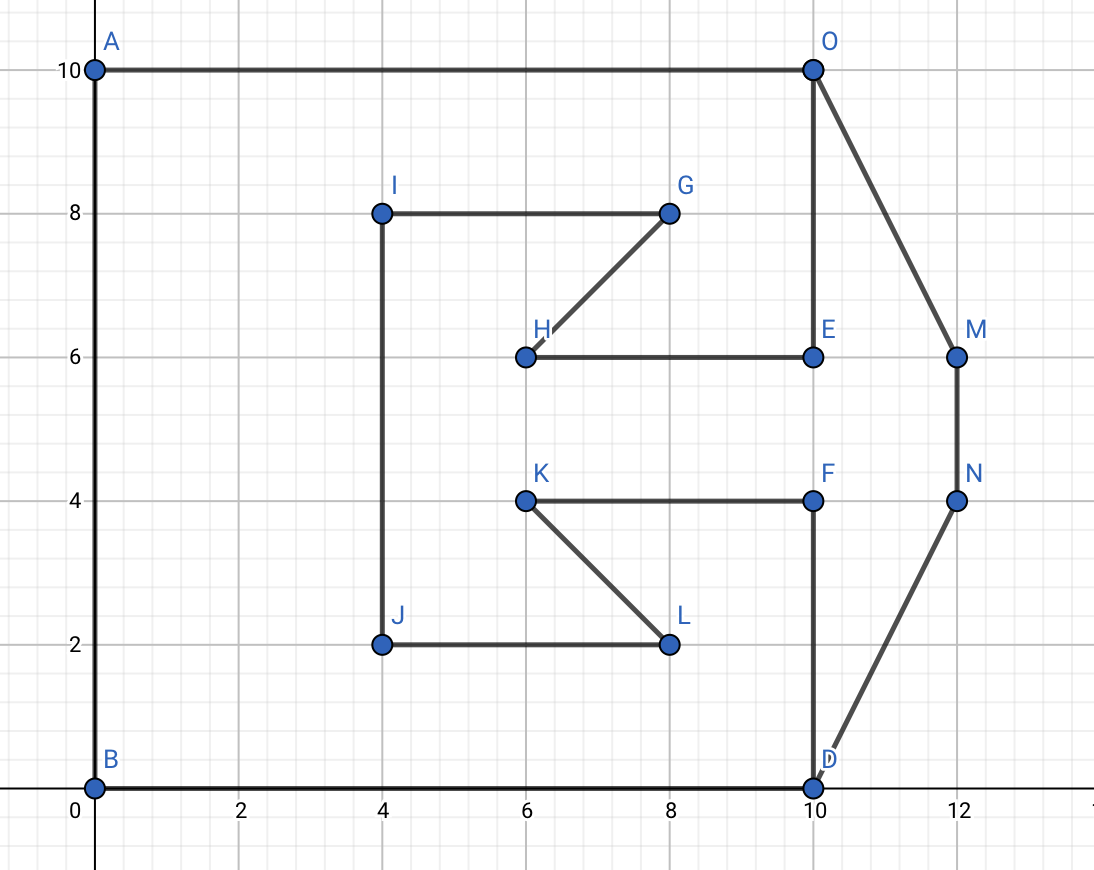

12 0 0 10 0 10 4 6 4 8 2 4 2 4 8 8 8 6 6 10 6 10 10 0 10 12 12 4 12 6 10 10 10 6 6 6 8 8 4 8 4 2 8 2 6 4 10 4 10 0 ans=1 12 0 0 10 0 10 4 6 4 8 2 4 2 4 8 8 8 6 6 10 6 10 10 0 10 8 12 4 12 6 6 6 8 8 4 8 4 2 8 2 6 4 ans=0
1 // ——By DD_BOND 2 3 //#include<bits/stdc++.h> 4 //#include<unordered_map> 5 //#include<unordered_set> 6 #include<functional> 7 #include<algorithm> 8 #include<iostream> 9 //#include<ext/rope> 10 #include<iomanip> 11 #include<climits> 12 #include<cstring> 13 #include<cstdlib> 14 #include<cstddef> 15 #include<cstdio> 16 #include<memory> 17 #include<vector> 18 #include<cctype> 19 #include<string> 20 #include<cmath> 21 #include<queue> 22 #include<deque> 23 #include<ctime> 24 #include<stack> 25 #include<map> 26 #include<set> 27 28 #define fi first 29 #define se second 30 #define pb push_back 31 #define MP make_pair 32 33 using namespace std; 34 35 typedef double db; 36 typedef long ll; 37 typedef pair<db,db> Pd; 38 typedef pair<int,int> P; 39 typedef pair<ll,ll> Pll; 40 41 const db eps=1e-6; 42 const int MAXN=1e3+10; 43 const db pi=acos(-1.0); 44 const ll INF=0x3f3f3f3f3f3f3f3f; 45 46 inline int dcmp(db x){ 47 if(fabs(x)<eps) return 0; 48 return (x>0? 1: -1); 49 } 50 51 inline db Sqrt(db x){ 52 return x>0? sqrt(x): 0; 53 } 54 55 inline db sqr(db x){ return x*x; } 56 57 struct Point{ 58 db x,y; 59 Point(){ x=0,y=0; } 60 Point(db _x,db _y):x(_x),y(_y){} 61 void input(){ 62 double _x,_y; 63 scanf("%lf%lf",&_x,&_y); 64 x=_x,y=_y; 65 } 66 bool operator ==(const Point &b)const{ 67 return (dcmp(x-b.x)==0&&dcmp(y-b.y)==0); 68 } 69 bool operator <(const Point &b)const{ 70 return (dcmp(x-b.x)==0? dcmp(y-b.y)<0 : x<b.x); 71 } 72 Point operator +(const Point &b)const{ 73 return Point(x+b.x,y+b.y); 74 } 75 Point operator -(const Point &b)const{ 76 return Point(x-b.x,y-b.y); 77 } 78 Point operator *(db a){ 79 return Point(x*a,y*a); 80 } 81 Point operator /(db a){ 82 return Point(x/a,y/a); 83 } 84 db len2(){ //长度平方 85 return sqr(x)+sqr(y); 86 } 87 db len(){ //长度 88 return Sqrt(len2()); 89 } 90 db polar(){ //向量的极角 91 return atan2(y,x); //返回与x轴正向夹角(-pi~pi] 92 } 93 Point change_len(db r){ //转化为长度为r的向量 94 db l=len(); 95 if(dcmp(l)==0) return *this; //零向量 96 return Point(x*r/l,y*r/l); 97 } 98 Point rotate(Point p,db ang){ //绕点p逆时针旋转ang度 99 Point v=(*this)-p; 100 db c=cos(ang),s=sin(ang); 101 return Point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c); 102 } 103 }; 104 105 inline db cross(Point a,Point b){ //叉积 106 return a.x*b.y-a.y*b.x; 107 } 108 109 inline db dot(Point a,Point b){ //点积 110 return a.x*b.x+a.y*b.y; 111 } 112 113 inline db dis(Point a,Point b){ //两点的距离 114 Point p=b-a; return p.len(); 115 } 116 117 db rad(Point a,Point b){ //两个向量的夹角 118 return fabs(atan2(fabs(cross(a,b)),dot(a,b))); 119 } 120 121 struct Node{ 122 Point vec,s,t; 123 Node(){} 124 Node(Point a,Point b,Point c){ 125 vec=a,s=b,t=c; 126 } 127 }; 128 129 Point a[210],b[210],tmp[410]; 130 131 int main(void){ 132 int n; 133 while(~scanf("%d",&n)){ 134 int ans=0; 135 for(int i=0;i<n;i++) a[i].input(),a[i+n]=a[i]; 136 int m; scanf("%d",&m); 137 for(int i=0;i<m;i++) b[i].input(),b[i+m]=b[i]; 138 139 for(int i=0;i<n;i++) 140 for(int j=0;j<m;j++) 141 if(dcmp(dis(a[i],a[i+1])-dis(b[j],b[j+1]))==0){ 142 int p=0,f=0; 143 vector<Node>st; 144 db ang=rad(b[j+1]-b[j],a[i+1]-a[i]); 145 if(dcmp(cross(b[j+1]-b[j],a[i+1]-a[i]))>=0) ang-=pi; 146 else ang=pi-ang; 147 148 for(int k=0;k<i;k++) tmp[p++]=a[k]; 149 for(int k=j+1;k<j+m+1;k++) tmp[p++]=a[i+1]+(b[k]-b[j]).rotate(Point(0,0),ang); 150 for(int k=i+2;k<n;k++) tmp[p++]=a[k]; 151 152 tmp[p]=tmp[0]; 153 154 for(int i=0;i<p;i++){ 155 Point res=tmp[i+1]-tmp[i]; 156 if(st.size()&&st.back().t==tmp[i]&&st.back().s==tmp[i+1]) st.pop_back(); 157 else st.pb(Node(res,tmp[i],tmp[i+1])); 158 } 159 160 st.pb(st[0]); 161 for(int i=1;i<(int)st.size();i++) 162 if(dcmp(cross(st[i-1].vec,st[i].vec))<0|| 163 (dcmp(cross(st[i-1].vec,st[i].vec))==0&&dcmp(dot(st[i-1].vec,st[i].vec))<=0)) 164 f=1; 165 if(!f) ans=1; 166 } 167 printf("%d\n",ans); 168 } 169 return 0; 170 }

