排序算法:快速排序
基本思想是:通过一趟排序将要排序的数据分割成独立的两部分:分割点左边都是比它小的数,右边都是比它大的数
学习一下排序算法中的快速排序!快速排序和冒泡排序差不多,都是通过比较元素的大小,然后进行相应的交换,不过快速排序的效率要比冒泡排序高的多,因为它将一个整体一分二,二分四 ,,,然后每个小整体再进行比对交换,这样效率会大大提高,就像做事情一样,把一个大事情分解,分别去做,效率肯定会更高些!
首先,对于一大堆无序的数字,从中随机挑选一个(通常都是第一个,或者最后一个),比如是53,这个被选上的数字被称为枢值/基准数(枢纽的枢),接下来,然后设立两个指针 i 和 j ,左边的为 i,右边的为 j ,然后将两个指针分别移动,左边的向右移动,右边的向左移动(如果基准数是第一个,那就先从右边开始比对,如果基准数是最后一个,那就先从第一个比对) 在移动的过程中,将每一个元素分别与基准数比对,左边的比对过程中如果比基准数小,不变,反之,交换(和原先空位置交换,因为在比对之前,将一个数拿出来作为基准数,所以作为基准数的那个位置就空了),右边的比对过程中如果比基准数大,不变,反之,交换,这样将所有要排序的数字分成两部分,一部分是大于等于枢值53的,一部分是小于枢值53的。在第一步完成后,一大堆无序的数字就变得稍微有序一点了。
第二步,从上面得到的两堆数字,分别采用第一步的方法各自再找一个枢值。对于第一堆,由于所有的数字都比53大,至少也等于53,因此,第二次随机挑选的枢值肯定是一个大于53的数字,比如79;类似地,对于第二堆,由于所有的数字都小于53,因此第二次随机挑选的枢值肯定小于它,比如4。接下来,再把两堆数字各自分成大于等于相应枢值的数字序列,以及小于枢值的数字序列。这样做下来,原来的一大堆数就变成了四小堆,它们分别是小于4的数字,介于4到53之间的,介于53到79之间的,以及大于或等于79的。
再接下来,用同样的方法,四堆变八堆,八堆变十六堆,很快所有的数字就排好序了。
图解:这个图非常详细,在一篇博客看到的,顺便说一下个人理解(小白学习中,理解错了大神们也别喷我(⊙o⊙)…)
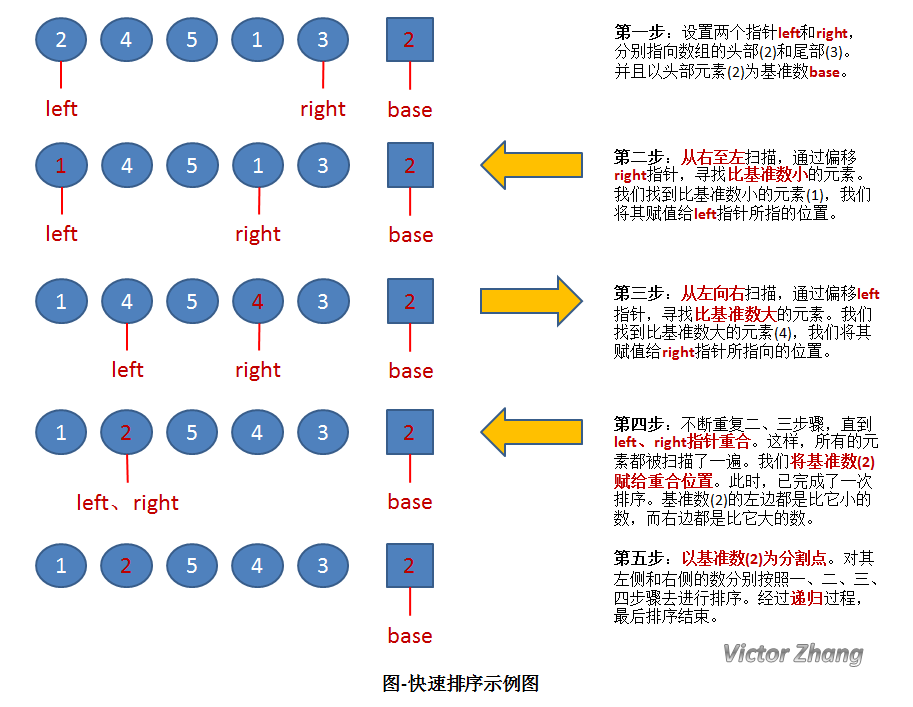
个人理解:在上图中,有一列无序数字,是2,4,5,1,3 要对它进行快速排序,让它变成有序数列
第一步:
先找出基准数为 “2” ,也就是数列的第一个元素(这时2 的位置就空了,就相当于有一排人,要对他们的身高进行排序,先让第一个人站到最前边,原先位置空出来)
第二步:
设立两个指针分别为 left 和 right (最左边和最右边)
第三步:
先移动 right 指针(因为基准数是第一个,这个位置是空的)向左移动,与基准数进行比对,如果比基准数大则不变,继续移动,如果比基准数小,则交换到原先基准数的位置(也就是第一个位置)第一个进行比对的是 “3” 、比基准数大 不变,接着移动到 “1” 、1 比基准数小,交换,这时原先基准数的位置的元素就是“1”,这个时候数列就是:1 4 5 1(这个1已经没有了,交换到第一个基准数位置了) 3
第四步:
再移动left指针(这个时候原先基准数的位置的元素就是从右边交换过来的首个比基准数小的元素 “1”)与基准数比对,指针从 元素“1” 移动到元素“4” 4比基准数大,则交换到原先元素“1”的位置
第五步:
不断重复三和四步骤,不停的移动left和right,当指针left和right和重合的时候,就将原先被抽出来的基准从放入到里边。这时,一个无序的数列就变得有序了,左边的都是比基准数“2”小的元素,而右边都是比基准数“2”大的元素!
第六步:
以原先基准数“2”为分割点,分别采用上边步骤进行排序,经过递归过程,最后排序结束(在程序里递归就是自己调用自己,不停重复,直到满足条件才能结束)
代码实例(C#版本)
将无序数组排序,并比较一下快速排序和冒泡排序的元素比较交换次数!
class Counts { public static int count1 = 0; public static int count2 = 0; } class Program { static void Main(string[] args) { int[] array = new int[20]; Random rand = new Random(); for (int i = 0; i < 20; i++) { array[i] = rand.Next(0, 100); } Console.WriteLine("排序前的数组:"); foreach (var item in array) { Console.Write("{0} ", item); } Console.WriteLine(); Console.WriteLine("冒泡排序后的数组:"); foreach (var item in Sort.PopSort(array)) { Console.Write("{0} ", item); } Console.WriteLine("\n快速排序后的数组:"); int[] arr = new int[array.Length]; array.CopyTo(arr, 0); Sort.QuickSort(arr, 0, arr.Length - 1); foreach (var item in arr) { Console.Write("{0} ", item); } Console.WriteLine("\n\n冒泡排序的比较次数:{0}\n快速排序的交换次数:{1}", Counts.count1, Counts.count2); Console.ReadLine(); } } static class Sort { /// <summary> /// 冒泡排序 /// </summary> /// <param name="array"></param> /// <returns></returns> public static int[] PopSort(int[] array) { int[] arr = new int[array.Length]; array.CopyTo(arr, 0); for (int i = 0; i < arr.Length; i++) { for (int j = 0; j < arr.Length - 1; j++) { if (arr[j] > arr[j + 1]) { int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; Counts.count1++; } else continue; } } return arr; } /// <summary> /// 快速排序 /// </summary> /// <param name="array"></param> /// <param name="left"></param> /// <param name="right"></param> /// <returns></returns> private static int sortUnit(int[] array, int left, int right) { //以left为基准数,数组第一个元素 int key = array[left]; while (left < right) { //因为基准数是第一个元素,所有从右边开始进行比对 while (array[right] >= key && right > left) { //比基准数大,不变,继续向左移动指针 --right; } array[left] = array[right]; Counts.count2++; while (array[left] <= key && right > left) { //比基准数小,不变,继续向右移动指针 ++left; } array[right] = array[left]; Counts.count2++; } //最后将基准数放到指针重合位置 array[left] = key; return right; } /// <summary> /// 快速排序 /// </summary> /// <param name="array">要排序的无序数组</param> /// <param name="left">指针left</param> /// <param name="right">指针right</param> public static void QuickSort(int[] array, int left, int right) { //重合就return 因为左边的要小于右边的 if (left >= right) { return; } //调用快速排序方法,将数组和指针传入 int index = sortUnit(array, left, right); //递归调用,分别对排序好的左右两小部分(左边小于原先基准数的数列 右边大于原先基准数的数列)进行重复步骤排序 QuickSort(array, left, index - 1);//左边 QuickSort(array, index + 1, right);//右边 } }
运行结果:
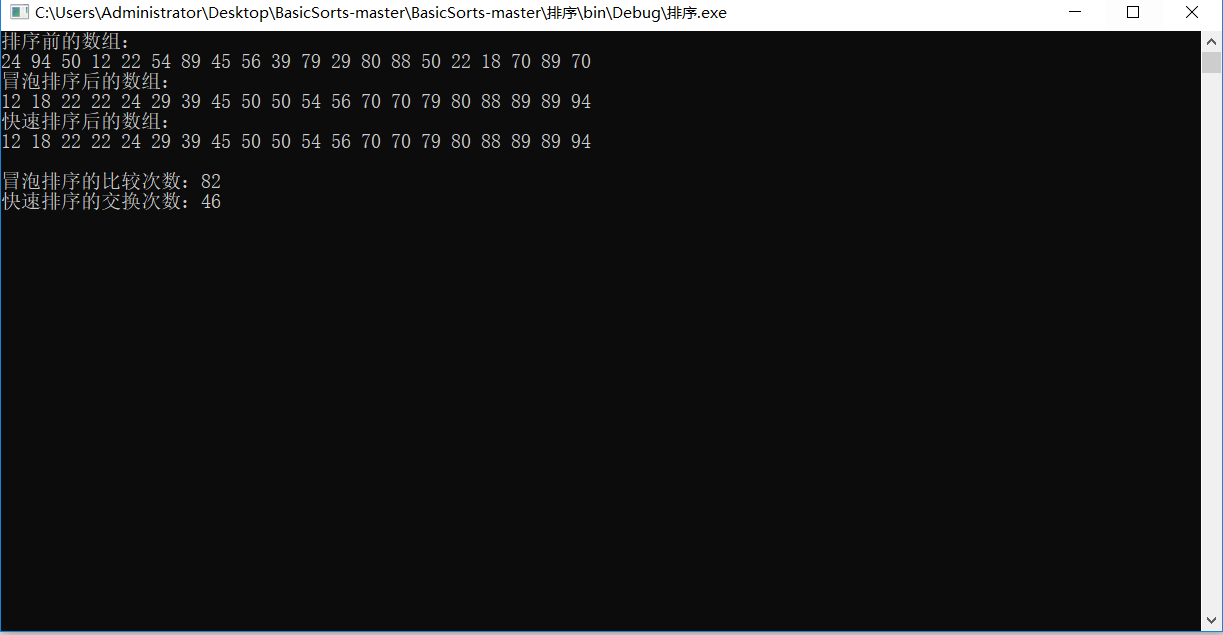
可以看出,快速排序的比较次数要比冒泡排序少很多!当然,这里数组中的元素比较少,如果是上千万,或者更大,那差别可就更明显了,可以说是量级的差别吧!
最后说一下我在吴老师(吴军博士)的谷歌方法论中学到的东西:世上没有绝对的最好,比如在生活中,从一个地方去另一个地方,A路线很近,很快,但是一旦遇到突发情况就需要很长时间,而B路比A路远一些,很慢,但是遇到突发情况比要A路遇到的突发情况要快很多!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号