最短路径——Bellman-Ford算法
转自:https://www.cnblogs.com/xzxl/p/7232929.html
一、相关定义
最短路径:求源点到某特定点的最短距离
特点:Bellman-Ford算法主要是针对有负权值的图,来判断该图中是否有负权回路或者存在最短路径的点
局限性:算法效率不高,不如SPFA算法
时间复杂度:O(mn)
具体与dijkstra算法的比较
Bellman-Ford算法为何需要循环n-1次来求解最短路径?Dijkstra从源点开始,更新dis[],找到最小值,再更新dis[]……每次循环都可以确定一个点的最短路。Bellman-Ford算法同样也是这样,它的每次循环也可以确定一个点的最短路,只不过代价很大,因为 Bellman-Ford每次循环都是操作所有边。既然代价这么大,相比Dijkstra 算法,Bellman-Ford算法还有啥用?因为后者可以检测负权回路啊。Bellman-Ford 算法的时间复杂度为 O(nm),其中 n 为顶点数,m 为边数。
负权回路
开始不懂,看了下面的图和我的算法描述后就懂了:
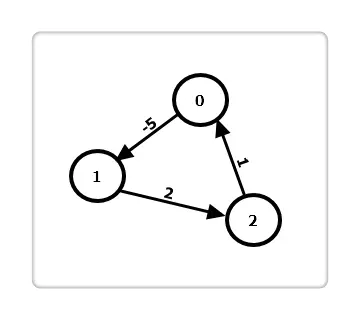
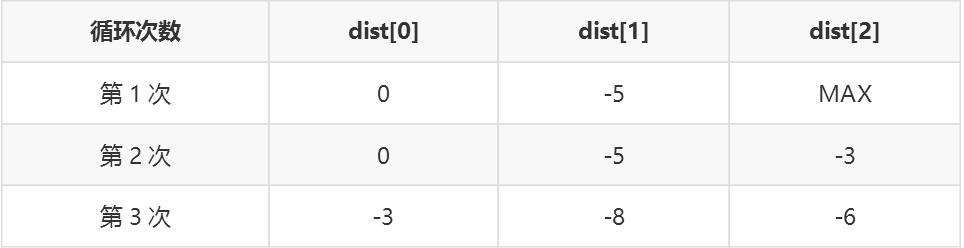
在循环n-1次的基础上再次遍历各边,对于所有边,只要存在一条边e(u, v)使得 dis[u] + w(u,v) < dis[v],则该图存在负权回路。
【松弛操作】


如左图所示,松弛计算之前,点B的值是8,但是点A的值加上边上的权重2,得到5,比点B的值(8)小,所以,点B的值减小为5。这个过程的意义是,找到了一条通向B点更短的路线,且该路线是先经过点A,然后通过权重为2的边,到达点B。
当然,如果出现右边这种情况,则不会修改点B的值,因为3+4>6。
二、算法描述
关键词:初始化 松弛操作
主要变量如下:
int n 表示有n个点,从1~n标号
int s,t s为源点,t为终点
int dis[N] dis[i]表示源点s到点i的最短路径
int pre[N] 记录路径,pre[i]表示i的前驱结点
bool vis[N] vis[i]=true表示点i被标记
初始化
dis数组全部赋值为INF,pre数组全部赋值为-1(表示还不知道前驱),
dis[s] = 0 表示源点不要求最短路径(或者最短路径就是0)。
松弛操作
对于每一条边e(u, v),如果dis[u] + w(u, v) < dis[v],则另dis[v] = dis[u]+w(u, v)。w(u, v)为边e(u,v)的权值
注:上述循环执行至多n-1次。若上述操作没有对Distant进行更新,说明最短路径已经查找完毕或者部分点不可达,跳出循环;否则执行下次循环。
检测负权回路
为了检测图中是否存在负环路,即权值之和小于0的环路。
检测的方法很简单,只需在求解最短路径的 n-1 次循环基础上,再进行第 n 次循环:对于每一条边e(u, v),如果存在边使得dis[u] + w(u, v) < dis[v],则图中存在负环路,即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。
小结
Bellman-Ford算法可以大致分为三个部分:
- 初始化所有点。每一个点保存一个值,表示从原点到达这个点的距离,将原点的值设为0,其它的点的值设为无穷大(表示不可达)。
- 进行循环,循环下标为从1到n-1(n等于图中点的个数)。在循环内部,遍历所有的边,进行松弛计算。
- 遍历途中所有的边(edge(u,v)),判断是否存在这样情况: d(v) > d (u) + w(u,v),若存在,则返回false,表示图中存在从源点可达的权为负的回路。
之所以需要第三步的原因,是因为,如果存在从源点可达的权为负的回路,则将因为无法收敛而导致不能求出最短路径。
三、代码实现
#include<iostream>
#include<stack>
using namespace std;
const int MAX = 10000; //假设权值最大不超过10000
struct Edge
{
int u;
int v;
int w;
};
Edge edge[10000]; //记录所有边
int dist[100]; //源点到顶点i的最短距离
int path[100]; //记录最短路的路径
int vertex_num; //顶点数
int edge_num; //边数
int source; //源点
bool BellmanFord()
{
//初始化
for (int i = 0; i < vertex_num; i++)
dist[i] = (i == source) ? 0 : MAX;
//n-1次循环求最短路径
for (int i = 1; i <= vertex_num - 1; i++)
{
for (int j = 0; j < edge_num; j++)
{
if (dist[edge[j].v] > dist[edge[j].u] + edge[j].w)
{
dist[edge[j].v] = dist[edge[j].u] + edge[j].w;
path[edge[j].v] = edge[j].u;
}
}
}
bool flag = true; //标记是否有负权回路
//第n次循环判断负权回路
for (int i = 0; i < edge_num; i++)
{
if (dist[edge[i].v] > dist[edge[i].u] + edge[i].w)
{
flag = false;
break;
}
}
return flag;
}
void Print()
{
for (int i = 0; i < vertex_num; i++)
{
if (i != source)
{
int p = i;
stack<int> s;
cout << "顶点 " << source << " 到顶点 " << p << " 的最短路径是: ";
while (source != p) //路径顺序是逆向的,所以先保存到栈
{
s.push(p);
p = path[p];
}
cout << source;
while (!s.empty()) //依次从栈中取出的才是正序路径
{
cout << "--" << s.top();
s.pop();
}
cout << " 最短路径长度是:" << dist[i] << endl;
}
}
}
int main()
{
cout << "请输入图的顶点数,边数,源点:";
cin >> vertex_num >> edge_num >> source;
cout << "请输入" << edge_num << "条边的信息:\n";
for (int i = 0; i < edge_num; i++)
cin >> edge[i].u >> edge[i].v >> edge[i].w;
if (BellmanFord())
Print();
else
cout << "Sorry,it have negative circle!\n";
return 0;
}
四、实战
https://acm.ecnu.edu.cn/problem/1817/
求出有 n (1<n<600) 个结点有向图中,结点 1 到结点 n 的最短路径。
输入格式
第一行有 2 个整数 n,m (0<m≤n(n−1)2),接下来 m 行每行有三个整数 u,v,w 结点 u 到 v 有一条权为 w 的边 (w<106)。
输出格式
输出结点 1 到结点 n 之间的最短路径,如果 1 到 n 之间不存在路径,输出 −1。
样例
input
3 3
1 2 10
2 3 15
1 3 30
output
25
AC代码
#include<iostream>
#include<vector>
using namespace std;
/**
* @brief Bellman-Ford单源最短路径算法
*
* @return int
*/
const int MAXN = 610;
const int MAXM = MAXN * MAXN;
const int INF = 1e6 + 10;
struct Edge{
int from, to;
int length;
Edge(int f, int t, int l): from(f), to(t), length(l) {}
};
vector<Edge> edges;
int dis[MAXN];
void Bellman_Ford(int start, int n, int m){
//初始化
for(int i = 1; i <= n; ++i){
dis[i] = INF;
}
dis[start] = 0;
//循环n-1次
for(int i = 1; i < n; ++i){
//对每一条边进行松弛操作
for(int j = 0; j < m; ++j){
int from = edges[j].from;
int to = edges[j].to;
int d = edges[j].length;
if(dis[from] + d < dis[to]){
dis[to] = dis[from] + d;
}
}
}
//判断是否存在负回路(再来一次遍历)
/*for(int j = 0; j < m; ++j){
int from = edges[j].from;
int to = edges[j].to;
int d = edges[j].length;
if(dis[from] + d < dis[to]){
return 0;
}
}
return 1;*/
}
int main(){
int n, m;
int from, to, length;
scanf("%d%d", &n, &m);
for(int i = 0; i < m; ++i){
scanf("%d%d%d", &from, &to, &length);
edges.push_back(Edge(from, to, length));
}
Bellman_Ford(1, n, m);
if(dis[n] == INF){
printf("-1\n");
}
else{
printf("%d\n", dis[n]);
}
//system("pause");
return 0;
}
五、遇到的坑
之前笔者学习别的单源最短路径代码的时候,了解到可将INF定义为INT_MAX,即如下代码
#include<climits>
const int INF = INT_MAX;
但是在提交题解时最后一个测试点通不过,查看测试数据input并进行测试,发现输出为-2147483575这个很离谱的结果。在将INF的定义改为如下形式,则顺利通过最后一个测试点。
const int INF = 1e6 + 10;
分析得出结论如下:
采用方案1,即INF = INT_MAX,当遇到dis[from]为INF的情况是,dis[from] + d超过INF,即超过int型整数所能表示的最大整数,也就是溢出了,则此时dis[from] + d的值变为等于或者接近INT_MIN,即int型整数所能表示的最小整数。此时,dis[to] > INT_MIN也就是 if判断条件必定满足,进而dis[to]就被赋值为一个接近或者等于INT_MIN的值,bug就由此产生。可能会导致终点的dis始终为接近或等于INT_MIN而得不到更新,也就是笔者测试时出现的-2147483575这样离谱的结果
用下面的列子说明一下:

input
3 3
2 3 15
1 2 10
1 3 30
| 1 | 2 | 3 | |
|---|---|---|---|
| Init | 0 | inf | inf |
| round1 edge1 | 0 | inf | -inf |
| round1 edge2 | 0 | 10 | -inf |
| round1 edge3 | 0 | 10 | -inf |
| round2 edge1 | 0 | 10 | -inf |
| round2 edge2 | 0 | 10 | -inf |
| round2 edge3 | 0 | 10 | -inf |
知道了哪里出现问题,修改就很容易了,只需要在if条件判断即可
if(dis[from] != INF && dis[from] + d < dis[v])
而定义为INF = 1e6 + 10,则不会出现这样的上述bug,原因是即便是dis[from]=INF,只要dis[from] + d没有超过int型变量所能表示的最大整数即可。但是此值需要根据题目描述来确定。
六、改进
《挑战程序设计竞赛》中关于Bellman Ford算法的代码如下:
若在n-1次的循环中,某一次遍历所有的边后,并没有更新dis,则算法运行结束
#include<iostream>
#include<vector>
#include<string.h>
#include<climits>
using namespace std;
/**
* @brief Bellman-Ford单源最短路径算法
*
* @return int
*/
const int MAXN = 610;
const int MAXM = MAXN * MAXN;
const int INF = INT_MAX;
struct Edge{
int from, to;
int length;
Edge(int f, int t, int l): from(f), to(t), length(l) {}
};
vector<Edge> edges;
int dis[MAXN];
void Bellman_Ford(int start, int n, int m){
//初始化
for(int i = 1; i <= n; ++i){
dis[i] = INF;
}
dis[start] = 0;
while(true){
//update标记此趟遍历是否有更新
bool update = false;
for(int i = 0; i < m; ++i){
Edge e = edges[i];
if(dis[e.from] != INF && dis[e.from] + e.length < dis[e.to]){
dis[e.to] = dis[e.from] + e.length;
update = true;
}
}
if(update == false){ //若此趟没有更新则算法结束
break;
}
}
}
bool find_negative_loop(int n, int m){
memset(dis, 0, sizeof(dis));
for(int i = 0; i < n; ++i){
for(int j = 0; j < m; ++j){
Edge e = edges[j];
if(dis[e.from] + e.length < dis[e.to]){
dis[e.to] = dis[e.from] + e.length;
if(i == n - 1){
return false;
}
}
}
}
return true;
}
int main(){
int n, m;
int from, to, length;
scanf("%d%d", &n, &m);
for(int i = 0; i < m; ++i){
scanf("%d%d%d", &from, &to, &length);
edges.push_back(Edge(from, to, length));
}
Bellman_Ford(1, n, m);
if(dis[n] == INF){
printf("-1\n");
}
else{
printf("%d\n", dis[n]);
}
system("pause");
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号