区间贪心问题小结(区间选点,区间覆盖,区间选取)
-
贪心算法
思想:什么是贪心算法,什么算得上是贪心
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
例题:
-
最少硬币问题 有1、2、5、10、20、50、100七种面值的硬币,要支付指定的金额,问怎么支付所用的硬币个数最少
策略:紧着最大分值换。
-
最大斜率问题 ,给出n个点的坐标(笛卡尔坐标) 求(A[i]-A[j])/(i-j)最大
策略:相邻的坐标中找到最大斜率
-
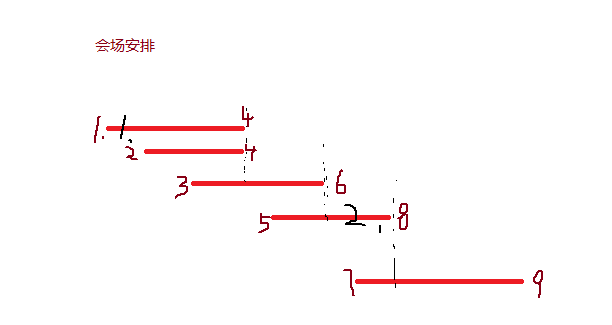
区间选取(会场安排问题),给一个大区间l,r然后给你n个区间,最最多多少个区间没有重复部分
例子:
学校的小礼堂每天都会有许多活动,有时间这些活动的计划时间会发生冲突,需要选择出一些活动进行举办。小刘的工作就是安排学校小礼堂的活动,每个时间最多安排一个活动。现在小刘有一些活动计划的时间表,他想尽可能的安排更多的活动,请问他该如何安排。
输入:
第一行是一个整型数m(m<100)表示共有m组测试数据。
每组测试数据的第一行是一个整数n(1<n<10000)表示该测试数据共有n个活动。
随后的n行,每行有两个正整数Bi,Ei(0<=Bi,Ei<10000),分别表示第i个活动的起始与结束时间(Bi<=Ei)输出:
对于每一组输入,输出最多能够安排的活动数量。
策略:每选一个之后能给后面的留更多的时间(效果:按结束时间排序)
那么第一个时,肯定选此时能选的结束时间最早的,选其他的话给后面留的时间都比前者小,所以咱们选的第一个肯定没错,就是此时能选的结束时间最早的,然后选第二个时,也是选可选时间中结束最早的,这样保证有其最优解,归纳起来激就是,每个根据当前可用时间,选取一个结束时间最早的,做为下一个会场的安排,
题目链接:http://acm.nyist.cf/problem/14
#include<stdio.h> #include<algorithm> using namespace std; const int maxn=10010; struct Node{ int beg,end; }node[maxn]; bool cmp(Node a,Node b) { return a.end<b.end; } int main() { int t,n,ans; scanf("%d",&t); while(t--) { scanf("%d",&n); for(int i=0;i<n;++i)//输入区间 并处理 { scanf("%d %d",&node[i].beg,&node[i].end); node[i].end++;//将区间变为左闭右开 } sort(node,node+n,cmp);//将区间按右端点排序,右端点小的在前面 ans=0; int pos=0;//初始化 //pos意为上一个选取的活动结束的位置,若果beg>=pos就可以安排 for(int i=0;i<n;++i) { if(node[i].beg>=pos) { ++ans; pos=node[i].end; } } printf("%d\n",ans); } } -
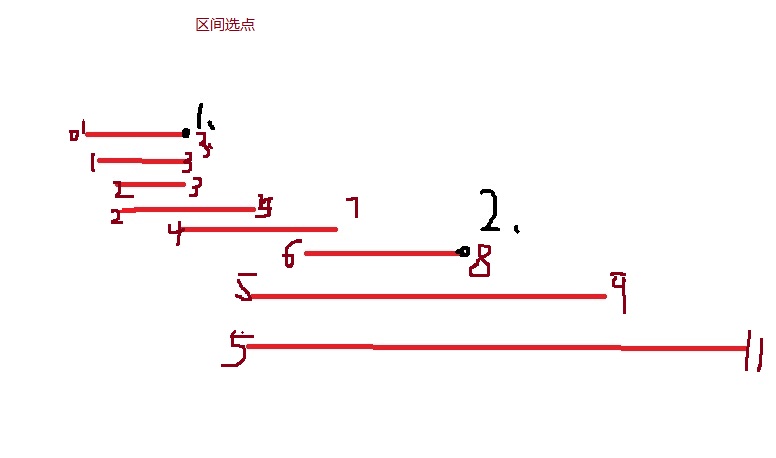
区间选点问题,n个闭区间[ai,bi],让他取尽量少的点,使得每个闭区间内至少有一个点。
输入:
n个闭区间,
输出:
最少用几个点,把每个区间都包含一个点
策略:让这个点出现在一个没有点的区间上,尽可能覆盖多的区间的地方**(效果:按结束处排序)**
首先为了将最左边的一个区间覆盖,(按结束排序即可)那么第一个点必须在第一个区间上,那么在区间上哪呢?为了让这个点让更多的区间的区间碰到,让这个点最靠右,这样的话能保证这个点覆盖的地方最多,然后一直往后遍历,直到一个区间不在这个点上时,为了让这个区间被覆盖,必须在从这个区间上找一点,(问题变为了前者) 每次一个点可以解决一个区间或者若干个区间,这遍历完所有区间即可
链接 http://nyoj.top/problem/891
代码:
#include<stdio.h> #include<algorithm> using namespace std; const int maxn=10010; struct Node{ int beg,end; }node[maxn]; bool cmp(Node a,Node b) { return a.end<b.end; } int main() { int n,ans; while(~scanf("%d",&n)) { for(int i=0;i<n;++i)//输入区间 并处理 { scanf("%d %d",&node[i].beg,&node[i].end); } sort(node,node+n,cmp);//将区间按右端点排序,右端点小的在前面 ans=0; int pos=-1;//pos代表第一个区间选取的点 for(int i=0;i<n;++i) { if(node[i].beg>pos) { pos=node[i].end; ++ans; } } printf("%d\n",ans); } } -
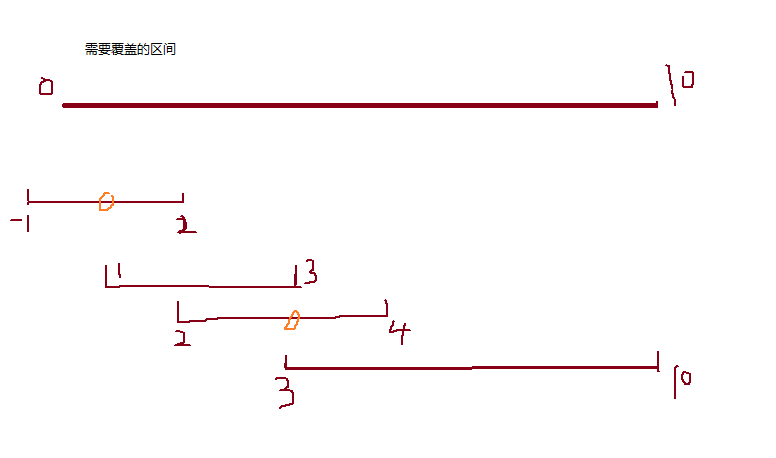
区间完全覆盖问题
问题描述:给定一个长度为m的区间(全部闭合),再给出n条线段的起点和终点(注意这里是闭区间),求最少使用多少条线段可以将整个区间完全覆盖
将所有区间化作此区间的区间,剪辑一下(没用的区间删除)
策略:在能连接区间左边的情况下,找到向右边扩展最长的位置。(效果:按开头排序,开头一样,右边最长的靠前)
为了连接到这个需要被覆盖区间的左边,选一个左端点最靠前的区间,如果左端点相同让右端点大的排在前面
然后向右扫描区间…,如何找下一个需要安置的区间呢,即直到找到与上一个区间没有连接的地方,这时候必须找一个区间来来作为一个连接,因为前面区间都没有断开,所以在前面扫描过的区间找到一个结束处最大的区间作为连接就行,记下这个能扩展到右边的最大位置(其实这个过程是找边的过程)。如果这个最大位置都不能连着,证明这个区间不能被完全覆盖!即不存在解。
代码:
#include<stdio.h> #include<string> #include<string.h> #include<stdlib.h> #include<algorithm> #include<math.h> using namespace std; const int maxn=10010; struct Node{ double beg,end; }node[maxn]; bool cmp(Node a,Node b) { if(a.beg==b.beg) return a.end>b.end; return a.beg<b.beg; } int main() { int t,n,cnt=0; double w,h; int ans=0; double x,r; scanf("%d",&t); while(t--) { scanf("%d %lf %lf",&n,&w,&h); cnt=0; while(n--) { scanf("%lf %lf",&x,&r); if(r<=h/2.0)//过滤掉无效的喷水装置 continue; double ll,rr;//存下该喷水装置区间的范围 double mid=sqrt(r*r-(h*h/4.0)); ll=x-mid; rr=x+mid;//将喷水装置转化为能覆盖的区间 ll=max(0.0,ll); rr=min((double)w,rr); node[cnt].beg=ll; node[cnt].end=rr; ++cnt; } /* 此时转化为一个区间覆盖问题 即在一个长度为w的区间内 选出最少的区间让这个区间覆盖 */ node[cnt].beg=(double)w; node[cnt].end=(double)w;//加入一个终端区间[w,w]这样遍历到整个区间最后会找出来一个往右边延伸到w的位置的区间,如果没有就没答案 ++cnt; sort(node,node+cnt,cmp); double maxpos,nowpos; nowpos=0.0; maxpos=0.0; int flag=1;// ans=0; for(int i=0;i<cnt;++i) { if(node[i].beg<=nowpos)//这个区间可以与前面的区间连着 maxpos=max(maxpos,node[i].end);//更新课扩展的最大区间 else { if(maxpos>=node[i].beg)//遇到一个间隔的 需要找一个区间补一下 { ans++; nowpos=maxpos; --i; } else//如果不能补 { flag=0; break;//无解 } } } if(flag) printf("%d\n",ans); else printf("0\n"); } }
-


