[NOIP补坑计划]NOIP2016 题解&做题心得
感觉16年好难啊QAQ,两天的T2T3是不是都放反了啊……
场上预计得分:100+80+100+100+65+100=545(省一分数线280)
ps:loj没有部分分,部分分见洛咕
题解:
D1T1 玩具谜题
水题送温暖~当然主要关注点都在mengbier和mogician上2333
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<cmath>
6 #include<queue>
7 #define inf 2147483647
8 #define eps 1e-9
9 using namespace std;
10 typedef long long ll;
11 int n,m,nw=0,x,op,a[100001];
12 char s[100001][11];
13 int main(){
14 scanf("%d%d",&n,&m);
15 for(int i=0;i<n;i++){
16 scanf("%d%s",&a[i],s[i]);
17 }
18 for(int i=1;i<=m;i++){
19 scanf("%d%d",&op,&x);
20 if(op^a[nw])nw=(nw+x)%n;
21 else nw=(nw+n-x)%n;
22 }
23 printf("%s",s[nw]);
24 return 0;
25 }
D1T2 天天爱跑步
绝对是这六题里最难的一题……这题目难度与顺序无关啊……想了半小时只会80,yy了一个线段树合并调不出来,树上差分并不会,最后百度了一发才搞懂……
首先考虑S->T这一条路径,肯定是从S出发先向上走到lca,再向下走到T,那么分开讨论这两种情况;
1.S->lca,此时路径上能对答案产生贡献的点i要满足$dep[i]+w[i]=dep[s]$;
2.lca->T,此时路径上能对答案产生贡献的点i要满足$dep[i]-w[i]=dep[t]-L$(其中L表示S到T的总长度)
这里貌似可以树链剖分+线段树直接维护?但是我出于对出题人基本的信任并没有写……
正解是用桶维护深度,维护一个向上的桶u和一个向下的桶d,对整棵树dfs;
对于一条s到t的路径,扫到s时就在s的$u[dep[s]]$中加一个,lca退栈时就把影响减掉,扫到lca时就在$d[dep[t]]$中加一个,t退栈时就减掉(这就是树上差分的思想);
那么每次的答案$ans[i]$就等于子树中$u[dep[i]+w[i]]+d[dep[i]-w[i]]$的数量;
注意这里可能会有负数,所以要整体加上$MAXN$;
最后如果s到t是一条链那么答案会算重,要把答案减一;
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<cmath>
6 #include<queue>
7 #define inf 2147483647
8 #define eps 1e-9
9 #define MX 300001
10 using namespace std;
11 typedef long long ll;
12 struct edge{
13 int v,next;
14 }a[600001];
15 int n,m,u,v,l,tot=0,fa[300001][20],ans[300001],bb[600001],bs[300001],bg[300001],dep[300001],ss[300001],t[300001],z[300001],num[300001],head[300001];
16 vector<int>s[300001],t1[300001],t2[300001];
17 void add(int u,int v){
18 a[++tot].v=v;
19 a[tot].next=head[u];
20 head[u]=tot;
21 }
22 void dfs(int u,int ff,int dpt){
23 fa[u][0]=ff;
24 dep[u]=dpt;
25 for(int i=1;i<=19;i++)fa[u][i]=fa[fa[u][i-1]][i-1];
26 for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){
27 int v=a[tmp].v;
28 if(v!=ff){
29 dfs(v,u,dpt+1);
30 }
31 }
32 }
33 int lca(int u,int v){
34 if(dep[u]<dep[v])swap(u,v);
35 int l=dep[u]-dep[v];
36 for(int i=19;i>=0;i--){
37 if((1<<i)&l){
38 u=fa[u][i];
39 }
40 }
41 if(u==v)return u;
42 for(int i=19;i>=0;i--){
43 if(fa[u][i]!=fa[v][i]){
44 u=fa[u][i],v=fa[v][i];
45 }
46 }
47 return fa[u][0];
48 }
49 void dfs1(int u,int ff){
50 int nw=bs[dep[u]+num[u]];
51 for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){
52 int v=a[tmp].v;
53 if(v!=ff){
54 dfs1(v,u);
55 }
56 }
57 bs[dep[u]]+=bg[u];
58 ans[u]+=bs[dep[u]+num[u]]-nw;
59 for(int i=0,ii=s[u].size();i<ii;i++){
60 bs[s[u][i]]--;
61 }
62 }
63 void dfs2(int u,int ff){
64 int nw=bb[dep[u]-num[u]+MX];
65 for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){
66 int v=a[tmp].v;
67 if(v!=ff){
68 dfs2(v,u);
69 }
70 }
71 for(int i=0,ii=t1[u].size();i<ii;i++){
72 bb[t1[u][i]+MX]++;
73 }
74 ans[u]+=bb[dep[u]-num[u]+MX]-nw;
75 for(int i=0,ii=t2[u].size();i<ii;i++){
76 bb[t2[u][i]+MX]--;
77 }
78 }
79 int main(){
80 memset(head,-1,sizeof(head));
81 scanf("%d%d",&n,&m);
82 for(int i=1;i<n;i++){
83 scanf("%d%d",&u,&v);
84 add(u,v);
85 add(v,u);
86 }
87 for(int i=1;i<=n;i++){
88 scanf("%d",&num[i]);
89 }
90 dfs(1,0,1);
91 for(int i=1;i<=m;i++){
92 scanf("%d%d",&ss[i],&t[i]);
93 z[i]=lca(ss[i],t[i]);
94 l=dep[ss[i]]+dep[t[i]]-2*dep[z[i]];
95 bg[ss[i]]++;
96 s[z[i]].push_back(dep[ss[i]]);
97 t1[t[i]].push_back(dep[t[i]]-l);
98 t2[z[i]].push_back(dep[t[i]]-l);
99 }
100 dfs1(1,0);
101 dfs2(1,0);
102 for(int i=1;i<=m;i++){
103 if(dep[z[i]]+num[z[i]]==dep[ss[i]])ans[z[i]]--;
104 }
105 for(int i=1;i<=n;i++){
106 printf("%d ",ans[i]);
107 }
108 return 0;
109 }
D1T3 换教室
题面看起来很复杂,实际上并不难……
显然这是个期望dp,且路程期望具有可加性,那么设$f[i][j][0 / 1]$表示当前在第i个时间段,已经申请了j次,这次是否申请;
推出式子就好了……
设$dis[i][j]$表示i到j的最短路:
$f[i][j][0]=min\{f[i-1][j][0]+dis[c[i-1]][c[i]],f[i-1][j][1]+dis[c[i-1]][c[i]]\times(1-k[i-1])$
$+dis[d[i-1]][c[i]]\times k[i-1]\}$
$f[i][j][1]=min\{f[i-1][j-1][0]+dis[c[i-1]][c[i]]\times(1-k[i])+dis[c[i-1]][d[i]]\times k[i],$
$f[i-1][j-1][1]+dis[c[i-1]][c[i]]\times(1-k[i-1])\times(1-k[i])+dis[d[i-1]][c[i]]\times k[i-1]\times(1-k[i])$
$+dis[c[i-1]][d[i]]\times(1-k[i-1])\times k[i]+dis[d[i-1]][d[i]]\times k[i-1]\times k[i]\}$
由于v很小,所以可以直接用floyd求出所有点对之间的最短路,于是就做完了……
时间复杂度$O(nm+V^3)$
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<cmath>
6 using namespace std;
7 int n,m,v,e,u,vv,w,c[2001],d[2001],sp[2001][2001];
8 double k[2000001],f[2001][2001][2],tt,ans;
9 int main(){
10 memset(sp,0x3f,sizeof(sp));
11 scanf("%d%d%d%d",&n,&m,&v,&e);
12 for(int i=1;i<=n;i++){
13 scanf("%d",&c[i]);
14 }
15 for(int i=1;i<=n;i++){
16 scanf("%d",&d[i]);
17 }
18 for(int i=1;i<=n;i++){
19 scanf("%lf",&k[i]);
20 }
21 for(int i=0;i<=v;i++){
22 sp[i][i]=0;
23 }
24 for(int i=0;i<=n;i++){
25 for(int j=0;j<=m;j++){
26 f[i][j][0]=1e16;
27 f[i][j][1]=1e16;
28 }
29 }
30 f[1][0][0]=f[1][1][1]=0;
31 for(int i=1;i<=e;i++){
32 scanf("%d%d%d",&u,&vv,&w);
33 if(u==vv){
34 continue;
35 }
36 sp[u][vv]=min(sp[u][vv],w);
37 sp[vv][u]=sp[u][vv];
38 }
39 for(int kk=1;kk<=v;kk++){
40 for(int i=1;i<=v;i++){
41 for(int j=1;j<=v;j++){
42 sp[i][j]=min(sp[i][kk]+sp[kk][j],sp[i][j]);
43 }
44 }
45 }
46 for(int i=2;i<=n;i++){
47 f[i][0][0]=f[i-1][0][0]+sp[c[i-1]][c[i]];
48 for(int j=1;j<=min(m,i);j++){
49 f[i][j][0]=min(f[i-1][j][0]+sp[c[i-1]][c[i]],f[i-1][j][1]+sp[c[i-1]][c[i]]*(1.0-k[i-1])+sp[d[i-1]][c[i]]*k[i-1]);
50 f[i][j][1]=f[i-1][j-1][0]+sp[c[i-1]][c[i]]*(1.0-k[i])+sp[c[i-1]][d[i]]*k[i];
51 tt=f[i-1][j-1][1]+sp[c[i-1]][c[i]]*(1.0-k[i-1])*(1.0-k[i])+sp[d[i-1]][c[i]]*k[i-1]*(1.0-k[i])+sp[c[i-1]][d[i]]*(1.0-k[i-1])*k[i]+sp[d[i-1]][d[i]]*k[i-1]*k[i];
52 f[i][j][1]=min(f[i][j][1],tt);
53 }
54 }
55 ans=f[n][0][0];
56 for(int i=1;i<=m;i++){
57 ans=min(ans,min(f[n][i][1],f[n][i][0]));
58 }
59 printf("%.2lf",ans);
60 return 0;
61 }
D2T1 组合数问题
并不是很水?要预处理前缀和;
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<cmath>
6 #include<queue>
7 #define inf 2147483647
8 #define eps 1e-9
9 using namespace std;
10 typedef long long ll;
11 int n,m,t,k,s[2001][2001],C[2001][2001];
12 int main(){
13 scanf("%d%d",&t,&k);
14 C[0][0]=1;
15 for(int i=1;i<=2000;i++){
16 C[i][0]=1;
17 for(int j=1;j<=i;j++){
18 C[i][j]=(C[i-1][j]+C[i-1][j-1])%k;
19 }
20 }
21 for(int i=1;i<=2000;i++){
22 for(int j=1;j<=2000;j++){
23 s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+(!C[i][j]&&i>=j);
24 }
25 }
26 while(t--){
27 scanf("%d%d",&n,&m);
28 printf("%d\n",s[n][m]);
29 }
30 return 0;
31 }
D2T2 蚯蚓
谁能给我解释一下这个鬼畜的部分分……
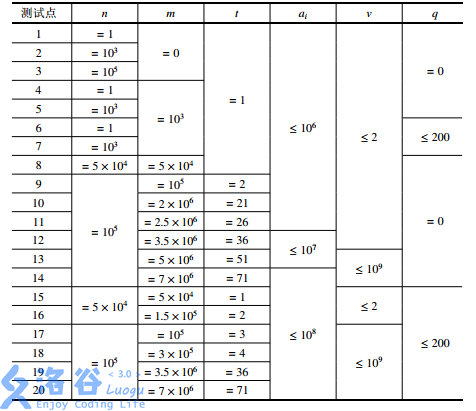
这题的难点在于阅读理解……题目写的很复杂,要仔细理解题意;
场上看到$M=7\times 10^6$直接虚掉……写了个优先队列65分滚粗了QAQ
注意到每次操作完整体增加q不好处理,因此可以考虑把q累加起来,每次计算完答案再加上总和,把分出来的两个数减去q即可,这样子做每次把分出来的数丢进优先队列就能拿到65分;
正解是非常巧妙的单调队列;
注意到这样子做所有没被拆分过的蚯蚓的长度是单调不增的,考虑被拆出来的两条新蚯蚓,由于拆分的两段比例都相等,所以较长那段和较短那段的长度也是单调不增的;
这样子可以只在开始排序一遍,开三个单调队列来分别维护$x$,$\lfloor px\rfloor$和$x-\lfloor px\rfloor$,每次选队头最大的进行操作即可;
想起来复杂,代码很短……
时间复杂度$O(nlogn+m)$
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<cmath>
6 #include<queue>
7 #define inf 1000000000000000
8 #define eps 1e-9
9 using namespace std;
10 typedef long long ll;
11 int n,m,q,t,l1=1,l2=1,l3=1,r1,r2=0,r3=0,id,num[100001],q1[100001],q2[7000001],q3[7000001];
12 ll t1,t2,u,v,ans,sum=0;
13 bool cmp(int a,int b){
14 return a>b;
15 }
16 int main(){
17 scanf("%d%d%d%lld%lld%d",&n,&m,&q,&u,&v,&t);
18 r1=n;
19 for(int i=1;i<=n;i++){
20 scanf("%d",&q1[i]);
21 }
22 sort(q1+1,q1+n+1,cmp);
23 for(int i=1;i<=m;i++){
24 id=0;
25 ans=-inf;
26 if(l1<=r1&&q1[l1]>ans){
27 ans=q1[l1];
28 id=1;
29 }
30 if(l2<=r2&&q2[l2]>ans){
31 ans=q2[l2];
32 id=2;
33 }
34 if(l3<=r3&&q3[l3]>ans){
35 ans=q3[l3];
36 id=3;
37 }
38 ans+=sum;
39 if(i%t==0)printf("%lld ",ans);
40 sum+=q;
41 t1=ans*u/v;
42 t2=ans-t1;
43 q2[++r2]=t1-sum;
44 q3[++r3]=t2-sum;
45 if(id==1)l1++;
46 else if(id==2)l2++;
47 else l3++;
48 }
49 puts("");
50 for(int i=1;i<=n+m;i++){
51 id=0;
52 ans=-inf;
53 if(l1<=r1&&q1[l1]>ans){
54 ans=q1[l1];
55 id=1;
56 }
57 if(l2<=r2&&q2[l2]>ans){
58 ans=q2[l2];
59 id=2;
60 }
61 if(l3<=r3&&q3[l3]>ans){
62 ans=q3[l3];
63 id=3;
64 }
65 if(i%t==0)printf("%lld ",ans+sum);
66 if(id==1)l1++;
67 else if(id==2)l2++;
68 else l3++;
69 }
70 return 0;
71 }
D2T3 愤怒的小鸟
暴力状压DP可过……(可能在考数学?)
预处理$g[i][j]$表示打第$i$和第$j$只猪的抛物线能打到哪些猪,然后状压表示当前打死了哪些猪;
显然$f[s|g[i][j]]=min\{f[s|g[i][j]],f[s]+1\}$
时间复杂度$O(n^22^n)$
ps:公式如下:
$y_1=ax_{1}^{2}+bx_1$
$y_2=ax_{2}^{2}+bx_2$
则$a=\frac{y_1x_2-x_1y_2}{x_1x_2(x_1-x_2)}$,$b=\frac{x_{1}^{2}y_2-x_{2}^{2}y_1}{x_1x_2(x_1-x_2)}$
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<cmath>
6 #include<queue>
7 #define inf 0x7f7f7f7f
8 #define eps 1e-9
9 using namespace std;
10 typedef long long ll;
11 struct pt{
12 double x,y;
13 }p[21];
14 int t,n,m,f[300001],nxt[21][21];
15 void pre(){
16 memset(nxt,0,sizeof(nxt));
17 for(int i=1;i<n;i++){
18 for(int j=i+1;j<=n;j++){
19 double x=p[i].x,y=p[i].y,xx=p[j].x,yy=p[j].y;
20 if(fabs(x-xx)<eps)continue;
21 double a=(y*xx-x*yy)/(x*xx*(x-xx)),b=(x*x*yy-xx*xx*y)/(x*xx*(x-xx));
22 if(a>-eps)continue;
23 for(int k=1;k<=n;k++){
24 double _x=p[k].x,_y=p[k].y;
25 if(fabs(a*_x*_x+b*_x-_y)<eps)nxt[i][j]|=(1<<k-1);
26 }
27 }
28 }
29 }
30 void work(){
31 memset(f,0x7f,sizeof(f));
32 f[0]=0;
33 for(int s=0;s<(1<<n);s++){
34 if(f[s]!=inf){
35 for(int i=1;i<=n;i++){
36 for(int j=i+1;j<=n;j++){
37 f[s|nxt[i][j]]=min(f[s|nxt[i][j]],f[s]+1);
38 }
39 f[s|(1<<i-1)]=min(f[s|(1<<i-1)],f[s]+1);
40 }
41 }
42 }
43 }
44 int main(){
45 scanf("%d",&t);
46 while(t--){
47 scanf("%d%d",&n,&m);
48 for(int i=1;i<=n;i++){
49 scanf("%lf%lf",&p[i].x,&p[i].y);
50 }
51 pre();
52 work();
53 printf("%d\n",f[(1<<n)-1]);
54 }
55 return 0;
56 }
总结:
我太菜了.jpg


