（WC2018模拟十二）【FJOI2016集训Day7T3】Xor-Mul棋盘

是不是应该第100篇博文纪念一下？

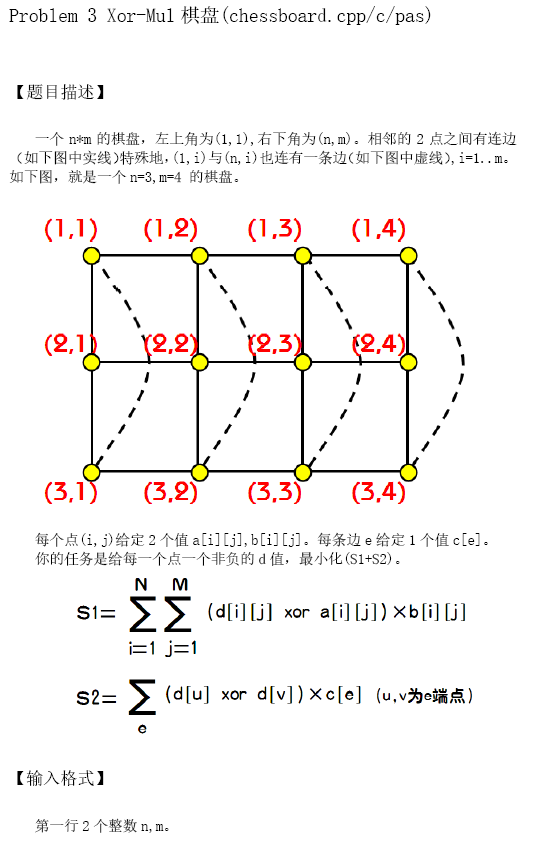
题解：

本质简单题。。。但是我没仔细看这题。。。

观察它的两个式子，都是xor完再乘以某个数，意味着d数组的每个二进制位对答案的贡献都是独立的，可以每一位分开处理。

由于每一列只和相邻的列有连边，每一列的点只有和相邻列的点的关系会对答案有影响（语文不好，感性理解），因此从左到右递推的话只用存最后一列的结果就行了；

由于n很小，用状压DP记录当前扫描线上的数字状态，逐格暴力转移即可。

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#define inf 1000000000000000
#define eps 1e-9
using namespace std;
typedef long long ll;
int N,n,m,a[6][10001],b[6][10001],e1[6][10001],e2[6][10001];
ll ans=0,tmp,f[2][51];
int chk(int a,int b){
    return (!b)?0:(a>>(b-1))&1;
}
int main(){
    scanf("%d%d",&n,&m);
    N=1<<n;
    for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&b[i][j]);
    for(int i=1;i<=n;i++)for(int j=2;j<=m;j++)scanf("%d",&e1[i][j]);
    for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&e2[i][j]);
    for(int t=0;t<=19;t++){
        memset(f[0],0,sizeof(f[0]));
        for(int i=1;i<=m;i++){
            for(int j=1;j<n;j++){
                for(int k=0;k<N;k++){
                    f[1][k]=min(f[0][k],f[0][k^(1<<j-1)]+e1[j][i])+((chk(k,j)==chk(k,j-1))?0:e2[j-1][i])+((chk(k,j)==chk(a[j][i],t+1))?0:b[j][i]);
                }
                memcpy(f[0],f[1],sizeof(f[1]));
            }
            for(int k=0;k<N;k++){
                f[1][k]=min(f[0][k],f[0][k^(1<<n-1)]+e1[n][i])+((chk(k,n)==chk(k,n-1))?0:e2[n-1][i])+((chk(k,n)==chk(k,1))?0:e2[n][i])+((chk(k,n)==chk(a[n][i],t+1))?0:b[n][i]);
            }
            memcpy(f[0],f[1],sizeof(f[1]));
        }
        tmp=inf;
        for(int j=0;j<N;j++){
            tmp=min(tmp,f[0][j]);
        }
        ans+=tmp*(1<<t);
    }
    printf("%lld\n",ans);
    return 0;
}