[arc082e]ConvexScore
题意：
给出直角坐标系中的$N$个点$(X_i,Y_i)$，定义由其中部分点构成的点集为“凸点集”当且仅当这些点恰好能构成一个凸多边形（内部没有其他点）。
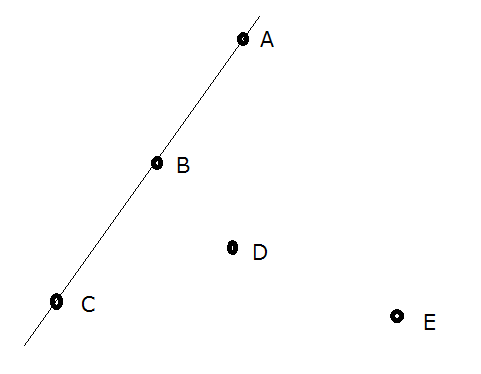
如图，点集$\{A,C,E\}$和$\{B,D,E\}$是凸点集，而$\{A,C,D,E\}$,$\{A,B,C,E\}$,$\{A,B,C\}$,$\{D,E\}$和$∅$则不是。
对于每个凸点集$S$，设这个凸点集内部（包括内部的点，所有顶点和边上的点）一共有$m$个点，那么它对答案的贡献就是$2^{m-|S|}$，求答案模998244353的结果。
$1\leq N\leq 200$
题解：
这题题面看起来很可怕。。。开始以为要写凸包的东西，看到那个998244353又以为是多项式相关。。。但是实际上这个模数是吓人的。。。理解了题意就非常好做了。
考虑一个凸点集$S$，设它内部的所有点组成的集合为$A$，显然$|A|=m$。那么有$2^{m-|S|}=2^{|A|-|S|}$。观察$|A|-|S|$这个式子，实际上表示的就是$S$内部不包括边界上的点的个数，即$|\complement_{A}S|$。那么$2^{m-|S|}$的实际意义就是$\complement_{A}S$的子集个数。至此题意就转化为在$\complement_{A}S$里随便选点，选出来之后再加上$S$，方案总数便是对答案的贡献。这些选点方案的共同点就是边界$S$是一样的，而凸点集内部的情况不同，换一种说法，就是这些点所能形成的凸包都是相同的。考虑原问题点集中的任意一个凸包，它对答案的贡献就是内部的点集的子集个数。然后我们惊奇的发现：这求的就是能形成凸包的点集个数！进一步，就是原点集中凸包的个数！
那么可以直接暴力。。。考虑不能形成凸包的情况，就是三个或以上的点共线，设有$(n+2)$个点共线，那么答案就会少$2^n$。原本点集中点数大于等于3的点集个数是$2^{n}-1-n-\binom{n}{2}$，再减去上面共线的情况减少的就行了。。。
$O(n^3)$搞定
代码：
1 #include<iostream>
2 #include<cstring>
3 #include<cstdio>
4 #include<cmath>
5 #define mod 998244353
6 using namespace std;
7 typedef long long ll;
8 int n,ans,x[501],y[501],pw[501];
9 int main(){
10 scanf("%d",&n);
11 pw[0]=1;
12 for(int i=1;i<=n;i++)pw[i]=(ll)pw[i-1]*2%mod;
13 for(int i=1;i<=n;i++)scanf("%d%d",&x[i],&y[i]);
14 ans=(pw[n]-n-1-n*(n-1)/2+mod)%mod;
15 for(int i=1;i<=n;i++){
16 for(int j=i+1;j<=n;j++){
17 int tmp=0;
18 for(int k=j+1;k<=n;k++){
19 if((y[j]-y[i])*(x[k]-x[j])==(y[k]-y[j])*(x[j]-x[i]))tmp++;
20 }
21 ans=(ans+mod+1-pw[tmp])%mod;
22 }
23 }
24 printf("%d",ans);
25 return 0;
26 }
人家真的没有抄代码！口亨QAQ
