【xsy2440】【GDOI2016】疯狂动物城
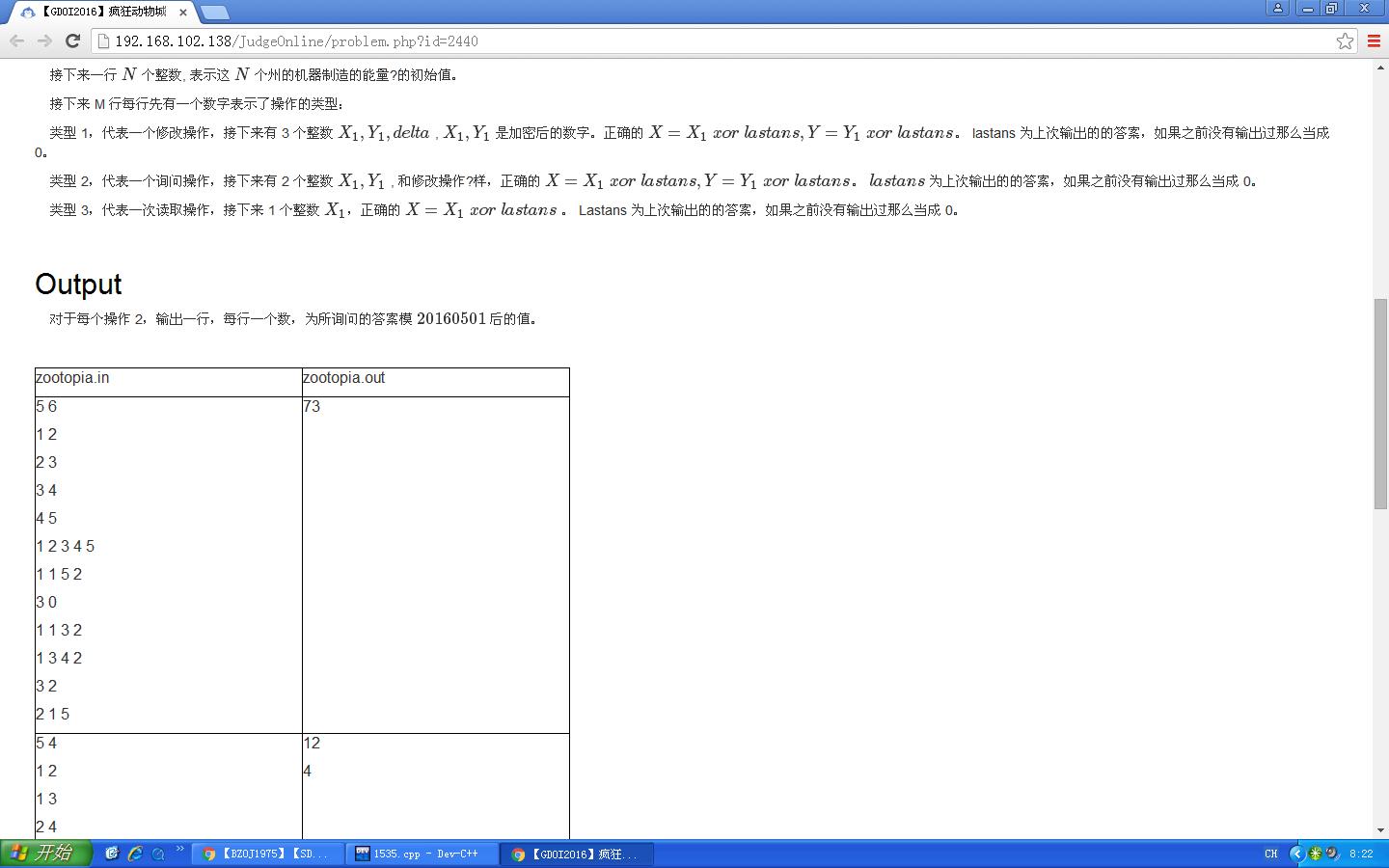
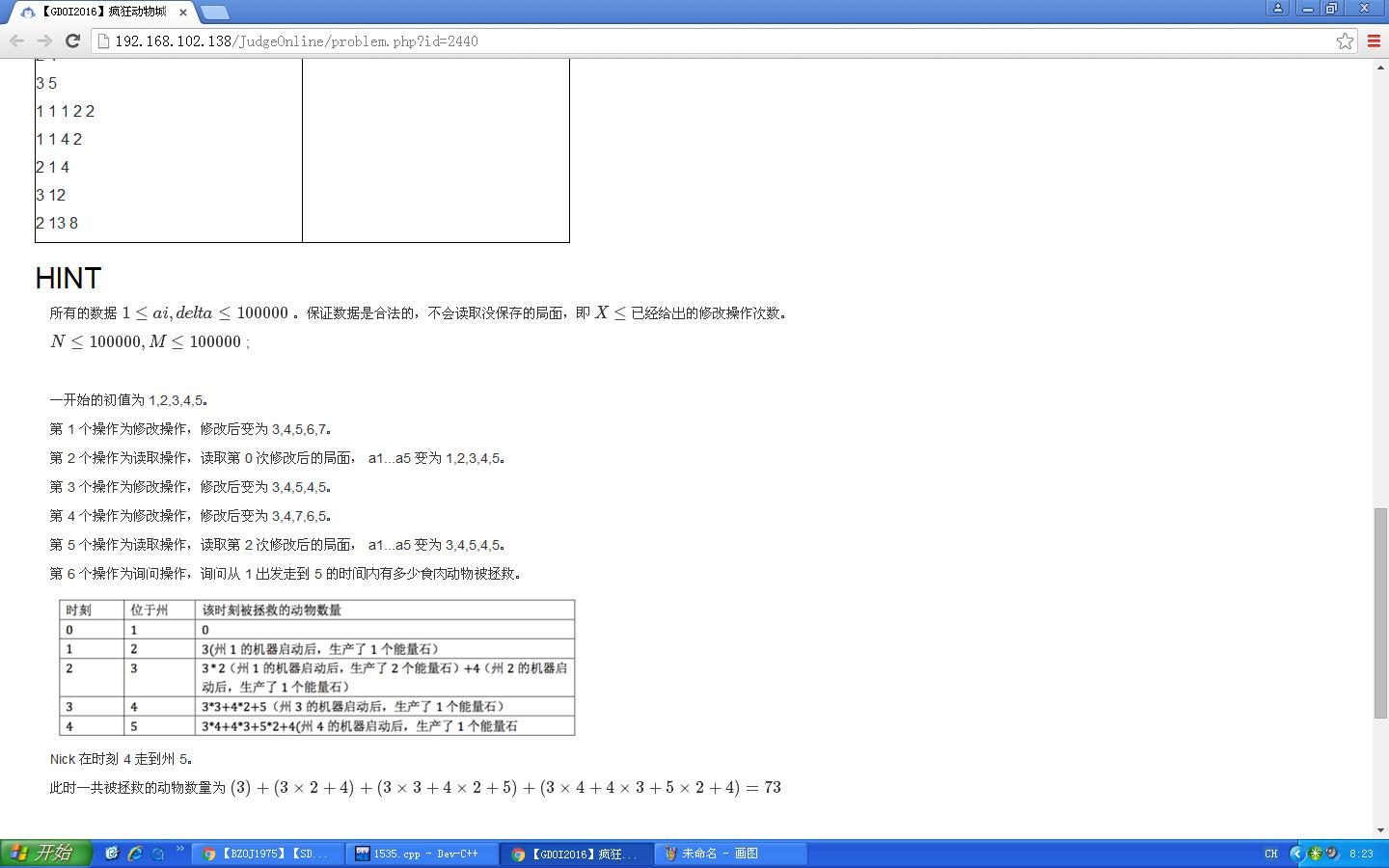
感受一下这恐怖的题目长度~~~
其实题意很裸,但是作为GDOI的一道防AK题,自然有他优秀的地方。
简化题意:给出一棵树,要求支持三个操作:
1.修改点值
2.询问点$x$到$y$之间的一些东东
3.回到某个版本之前
可持久化,强制在线。
考虑拆一下询问
如果把$x$到$y$路径上的所有点值放到一个数组$a$里,那么询问式子就是:
$\sum\limits_{i=1}^{n}a[i]\times\sum\limits_{j=1}^{n-i}j$
$=\sum\limits_{i=1}^{n}a[i]\times\frac{(n-i+1)\times(n-i)}{2}$
$=\sum\limits_{i=1}^{n}a[i]\times i^{2}-a[i]\times(2n+1)+a[i]\times n\times(n+1)$
发现$a[i]$,$a[i]\times i$,$a[i]\times i^2$都是常系数,于是就可以快乐维护了~
外面的很容易想到,树链剖分+可持久化线段树,单点修改即可。
可以感觉到逐渐膨胀的代码量>_<
注意到有左右方向的区别,要写两遍
代码量起飞了>_<
5000B刷新最长代码记录
注意:记得取模,随时爆int;
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #define mod 20160501 6 using namespace std; 7 typedef long long ll; 8 struct edge{ 9 int v,next; 10 }a[500001]; 11 struct data{ 12 ll s,a1,a2,s1,s2,ls,rs,lz,vv; 13 }t[5000001]; 14 ll n,m,u,v,w,ord,tim=0,tot=0,tote=0,ans=0,nrt=0,nowrt=0,last=0,ans1[2],ans2[2],head[1000001],rt[1000001],num[1000001],nmd[1000001],dep[1000001],top[1000001],siz[1000001],dfn[1000001],son[1000001],fa[1000001]; 15 void add(int u,int v){ 16 a[++tote].v=v; 17 a[tote].next=head[u]; 18 head[u]=tote; 19 } 20 void dfs1(int u,int f,int dpt){ 21 fa[u]=f; 22 dep[u]=dpt; 23 siz[u]=1; 24 for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){ 25 int v=a[tmp].v; 26 if(v==f)continue; 27 dfs1(v,u,dpt+1); 28 siz[u]+=siz[v]; 29 if(son[u]==-1||siz[v]>siz[son[u]])son[u]=v; 30 } 31 } 32 void dfs2(int u,int nowtp){ 33 top[u]=nowtp; 34 dfn[u]=++tim; 35 nmd[tim]=u; 36 if(son[u]==-1)return; 37 dfs2(son[u],nowtp); 38 for(int tmp=head[u];tmp!=-1;tmp=a[tmp].next){ 39 int v=a[tmp].v; 40 if(v==son[u]||v==fa[u])continue; 41 dfs2(v,v); 42 } 43 } 44 void pushup(int u){ 45 t[u].s=(t[t[u].ls].s+t[t[u].rs].s)%mod; 46 t[u].a1=(t[t[u].ls].a1+t[t[u].rs].a1)%mod; 47 t[u].a2=(t[t[u].ls].a2+t[t[u].rs].a2)%mod; 48 t[u].s1=(t[t[u].ls].s1+t[t[u].rs].s1)%mod; 49 t[u].s2=(t[t[u].ls].s2+t[t[u].rs].s2)%mod; 50 } 51 void build(int l,int r,int u){ 52 if(l==r){ 53 t[u].s=num[nmd[l]]; 54 t[u].a1=dep[nmd[l]]; 55 t[u].a2=(t[u].a1*t[u].a1)%mod; 56 t[u].s1=(t[u].s*t[u].a1)%mod; 57 t[u].s2=(t[u].s*t[u].a2)%mod; 58 return; 59 } 60 int mid=(l+r)/2; 61 build(l,mid,t[u].ls=++tot); 62 build(mid+1,r,t[u].rs=++tot); 63 pushup(u); 64 } 65 void updata(int l,int r,int u,int L,int R,int lst,ll v){ 66 if(u==tot)t[u]=t[lst]; 67 if(l==L&&r==R){ 68 t[u].ls=t[lst].ls; 69 t[u].rs=t[lst].rs; 70 t[u].lz=(t[u].lz+v)%mod; 71 t[u].s1=(t[u].s1+t[u].a1*v)%mod; 72 t[u].s2=(t[u].s2+t[u].a2*v)%mod; 73 t[u].s=(t[u].s+v*(r-l+1))%mod; 74 t[u].vv=(t[u].vv+v)%mod; 75 return; 76 } 77 int mid=(l+r)/2; 78 if(R<=mid){ 79 if(t[u].rs<=last)t[u].rs=t[lst].rs; 80 if(t[u].ls<=last)t[u].ls=++tot; 81 updata(l,mid,t[u].ls,L,R,t[lst].ls,v); 82 }else if(mid<L){ 83 if(t[u].ls<=last)t[u].ls=t[lst].ls; 84 if(t[u].rs<=last)t[u].rs=++tot; 85 updata(mid+1,r,t[u].rs,L,R,t[lst].rs,v); 86 }else{ 87 if(t[u].ls<=last)t[u].ls=++tot; 88 updata(l,mid,t[u].ls,L,mid,t[lst].ls,v); 89 if(t[u].rs<=last)t[u].rs=++tot; 90 updata(mid+1,r,t[u].rs,mid+1,R,t[lst].rs,v); 91 } 92 t[u].s1=(t[t[u].ls].s1+t[t[u].rs].s1+t[u].a1*t[u].vv%mod)%mod; 93 t[u].s2=(t[t[u].ls].s2+t[t[u].rs].s2+t[u].a2*t[u].vv%mod)%mod; 94 t[u].s=(t[t[u].ls].s+t[t[u].rs].s+t[u].vv*(r-l+1)%mod)%mod; 95 } 96 void getans(int u,int b,ll lz,ll v){ 97 ans=(ans+t[u].s2+lz*t[u].a2%mod)%mod; 98 ans1[b]=(ans1[b]+t[u].s1+t[u].a1*lz%mod)%mod; 99 ans2[b]=(ans2[b]+t[u].s+v*lz%mod)%mod; 100 } 101 void query(int l,int r,int u,int L,int R,int b,ll lz){ 102 if(!u)return; 103 lz+=t[u].vv; 104 if(l==L&&r==R){ 105 lz-=t[u].lz; 106 getans(u,b,lz,r-l+1); 107 return; 108 } 109 int mid=(l+r)/2; 110 if(R<=mid)query(l,mid,t[u].ls,L,R,b,lz); 111 else if(mid<L)query(mid+1,r,t[u].rs,L,R,b,lz); 112 else{ 113 query(l,mid,t[u].ls,L,mid,b,lz); 114 query(mid+1,r,t[u].rs,mid+1,R,b,lz); 115 } 116 } 117 void work(int t,int t1,int u,int v,ll w){ 118 while(top[u]!=top[v]){ 119 if(dep[top[u]]<dep[top[v]])swap(u,v); 120 updata(1,n,rt[t],dfn[top[u]],dfn[u],rt[t1],w); 121 u=fa[top[u]]; 122 } 123 if(dep[u]>dep[v])swap(u,v); 124 updata(1,n,rt[t],dfn[u],dfn[v],rt[t1],w); 125 } 126 int work1(int t,int u,int v){ 127 while(top[u]!=top[v]){ 128 if(dep[top[u]]>dep[top[v]]){ 129 query(1,n,rt[t],dfn[top[u]],dfn[u],0,0); 130 u=fa[top[u]]; 131 }else{ 132 query(1,n,rt[t],dfn[top[v]],dfn[v],1,0); 133 v=fa[top[v]]; 134 } 135 } 136 if(dep[u]>dep[v]){ 137 query(1,n,rt[t],dfn[v],dfn[u],0,0); 138 return v; 139 }else{ 140 query(1,n,rt[t],dfn[u],dfn[v],1,0); 141 return u; 142 } 143 } 144 int main(){ 145 memset(son,-1,sizeof(son)); 146 memset(head,-1,sizeof(head)); 147 scanf("%lld%lld",&n,&m); 148 for(int i=1;i<n;i++){ 149 scanf("%lld%lld",&u,&v); 150 add(u,v); 151 add(v,u); 152 } 153 for(int i=1;i<=n;i++)scanf("%lld",&num[i]); 154 dfs1(1,0,1); 155 dfs2(1,1); 156 rt[0]=tot=1; 157 build(1,n,rt[0]); 158 for(int i=1;i<=m;i++){ 159 scanf("%lld",&ord); 160 if(ord==1){ 161 scanf("%lld%lld%lld",&u,&v,&w); 162 u^=ans; 163 v^=ans; 164 last=tot; 165 rt[++nrt]=++tot; 166 work(nrt,nowrt,u,v,w); 167 nowrt=nrt; 168 }else if(ord==2){ 169 scanf("%lld%lld",&u,&v); 170 u^=ans; 171 v^=ans; 172 ans=ans1[0]=ans1[1]=ans2[0]=ans2[1]=0; 173 int t=dep[v]-dep[work1(nowrt,u,v)]*2; 174 ans=(ans+ans1[0]*(t*2+1)%mod+ans2[0]*t%mod*(t+1)%mod)%mod; 175 ans=(ans-ans1[1]*(dep[v]*2+1)%mod+ans2[1]*dep[v]%mod*(dep[v]+1)%mod+mod)%mod; 176 ans=(ans*10080251)%(ll)mod; 177 ans=(ans+mod)%mod; 178 printf("%lld\n",ans); 179 }else{ 180 scanf("%lld",&u); 181 u^=ans; 182 nowrt=u; 183 } 184 } 185 return 0; 186 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号