【XSY3306】alpha - 线段树+分治NTT
题目来源:noi2019模拟测试赛(一)
题意:

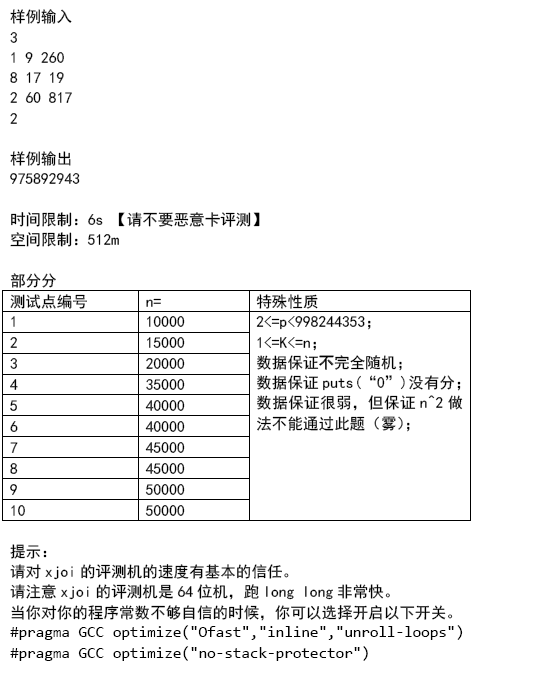
题解:
这场三道神仙概率期望题……orzzzy
这题暴力$O(n^2)$有30分,但貌似比正解更难想……(其实正解挺好想的)
注意到一次操作实际上就是在一段区间里乘上了一个形如$px+(1-p)$的多项式,设把所有多项式合并得到一个多项式$F(x)$,那么我们要求的答案实际上就是:
$$[x^k]F(x)$$
那么可以先离散化坐标,然后开一棵线段树,用vector维护每个点(即最小不可再分的区间)上要乘的多项式,最后dfs一遍线段树,用分治NTT合并每个点自身的多项式,再合并子树的多项式即可。
时间复杂度$O(nlog^3n)$
口胡起来很简单但是写起来很恶心……
代码:
NTT写的挫,人傻自带大常数,跑了4.3s
1 #include<algorithm>
2 #include<iostream>
3 #include<cstring>
4 #include<cstdio>
5 #include<vector>
6 #include<cmath>
7 #include<queue>
8 #define inf 2147483647
9 #define eps 1e-9
10 #define mod 998244353
11 #define G 3
12 using namespace std;
13 typedef long long ll;
14 typedef double db;
15 struct task{
16 int l,r,p;
17 }t[50001];
18 struct node{
19 int l,r;
20 }tr[400001];
21 int n,k,cnt=0,tn=0,nw[10],tmp[100001],lsh[100001],ans[50][50001];
22 vector<int>v[400001];
23 namespace Poly{
24 namespace NTT{
25 int bit,bitnum,rev[200001],W[200001][2];
26 int fastpow(int x,int y){
27 int ret=1;
28 for(;y;y>>=1,x=(ll)x*x%mod){
29 if(y&1)ret=(ll)ret*x%mod;
30 }
31 return ret;
32 }
33 void pre(){
34 int rG=fastpow(G,mod-2);
35 for(int i=1;i<=17;i++){
36 W[1<<i][0]=fastpow(G,(mod-1)/(1<<i));
37 W[1<<i][1]=fastpow(rG,(mod-1)/(1<<i));
38 }
39 }
40 void getr(int l){
41 for(bit=1,bitnum=0;bit<l;bit<<=1,bitnum++);
42 for(int i=1;i<bit;i++){
43 rev[i]=(rev[i>>1]>>1)|((i&1)<<(bitnum-1));
44 }
45 }
46 void ntt(int *s,int op){
47 for(int i=1;i<bit;i++){
48 if(i<rev[i])swap(s[i],s[rev[i]]);
49 }
50 for(int i=1;i<bit;i<<=1){
51 int w=W[i<<1][op==-1];
52 for(int p=i<<1,j=0;j<bit;j+=p){
53 int wk=1;
54 for(int k=j;k<i+j;k++,wk=(ll)wk*w%mod){
55 int x=s[k],y=(ll)s[k+i]*wk%mod;
56 s[k]=(x+y)%mod;
57 s[k+i]=(x-y+mod)%mod;
58 }
59 }
60 }
61 if(op==-1){
62 int rb=fastpow(bit,mod-2);
63 for(int i=0;i<bit;i++){
64 s[i]=(ll)s[i]*rb%mod;
65 }
66 }
67 }
68 }
69 int A[200001],B[200001];
70 void getmul(int *s,int *a,int *b,int len1,int len2){
71 for(int i=0;i<=len1;i++)A[i]=a[i];
72 for(int i=0;i<=len2;i++)B[i]=b[i];
73 NTT::getr((len1+len2)*2);
74 for(int i=len1+1;i<NTT::bit;i++)A[i]=0;
75 for(int i=len2+1;i<NTT::bit;i++)B[i]=0;
76 NTT::ntt(A,1);
77 NTT::ntt(B,1);
78 for(int i=0;i<NTT::bit;i++){
79 s[i]=(ll)A[i]*B[i]%mod;
80 }
81 NTT::ntt(s,-1);
82 }
83 void mul(int l,int r,int nw,int *s){
84 if(l==r){
85 s[0]=(mod-v[nw][l]+1);
86 s[1]=v[nw][l];
87 return;
88 }
89 int mid=(l+r)/2;
90 mul(l,mid,nw,s);
91 mul(mid+1,r,nw,s+mid-l+3);
92 getmul(s,s,s+mid-l+3,mid-l+1,r-mid);
93 }
94 }
95 void updata(int l,int r,int u,int L,int R,int p){
96 if(L<=tr[l].l&&tr[r].r<=R){
97 v[u].push_back(p);
98 return;
99 }
100 int mid=(l+r)/2;
101 if(L<=tr[mid].r)updata(l,mid,u*2,L,R,p);
102 if(tr[mid+1].l<=R)updata(mid+1,r,u*2+1,L,R,p);
103 }
104 int dfs(int l,int r,int u,int x){
105 int mid=(l+r)/2,L,R,mx;
106 if(l<r){
107 L=dfs(l,mid,u*2,x);
108 R=dfs(mid+1,r,u*2+1,x+1);
109 mx=max(L,R);
110 }
111 if(v[u].size()){
112 Poly::mul(0,v[u].size()-1,u,tmp);
113 }else tmp[0]=1;
114 if(l==r){
115 nw[0]=(tr[l].r-tr[l].l+1);
116 Poly::getmul(ans[x],nw,tmp,0,v[u].size());
117 return v[u].size();
118 }
119 for(int i=L+1;i<=mx;i++)ans[x][i]=0;
120 for(int i=R+1;i<=mx;i++)ans[x+1][i]=0;
121 for(int i=0;i<=mx;i++){
122 ans[x][i]=(ans[x][i]+ans[x+1][i])%mod;
123 }
124 Poly::getmul(ans[x],ans[x],tmp,mx,v[u].size());
125 return v[u].size()+mx;
126 }
127 int main(){
128 scanf("%d",&n);
129 Poly::NTT::pre();
130 for(int i=1;i<=n;i++){
131 scanf("%d%d%d",&t[i].l,&t[i].r,&t[i].p);
132 lsh[++cnt]=t[i].l;
133 lsh[++cnt]=t[i].r+1;
134 }
135 scanf("%d",&k);
136 lsh[++cnt]=1;
137 lsh[++cnt]=233333333;
138 sort(lsh+1,lsh+cnt+1);
139 cnt=unique(lsh+1,lsh+cnt+1)-lsh-1;
140 for(int i=2;i<=cnt;i++){
141 tr[++tn].l=lsh[i-1];
142 tr[tn].r=lsh[i]-1;
143 }
144 for(int i=1;i<=n;i++){
145 updata(1,tn,1,t[i].l,t[i].r,t[i].p);
146 }
147 dfs(1,tn,1,0);
148 printf("%d",ans[0][k]);
149 return 0;
150 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号