wqs二分 学习笔记
wqs二分
参考资料
【学习笔记】WQS二分详解及常见理解误区解释 -ikrvxt -CSDN
wqs二分 学习笔记 -Leap_Frog -Luogu
wqs二分详解 -Hypoc_ -CSDN
前言
2024.08.13
模拟赛遇到恰好选 \(m\) 个的限制的反悔贪心做模拟费用流的题,然而不会wqs二分,改不完题,于是赶快学习wqs二分,遂要写下此文。
关键词
恰好选 \(m\) 个,凸性,二分斜率。
引入
有这样一类问题:
有 \(n\) 个物品,你要从中选出恰好 \(m\) 个物品,选的时候带有一些限制,选了一个物品后能获得价值,要求价值和最大。
同时这一类问题的特点是,如果没有 \(m\) 的限制,也就是选任意多个,能容易求得,可以是用贪心或是 DP 之类的。
然而当有 \(m\) 的限制时,我们就不能快速求得。
此时可以考虑 wqs二分 优化。
用时有一个前提:
设 \(g(i)\) 表示恰好选 \(i\) 个的答案,若将 \((i,g(i))\) 画在平面上并连线,要满足它是一个凸包(上凸或下凸),即这些边的斜率有单调性。
表示成代数意义就是:\(g(i)-g(i-1)\ge g(i+1)-g(i)\)。
实际意义就是:一开始选最优的,然后选最优和次优的,然后越来越不优,到后面就开始下降。
然而我们实际并不知道谁更优,只知道答案是凸性。
例如像这样:
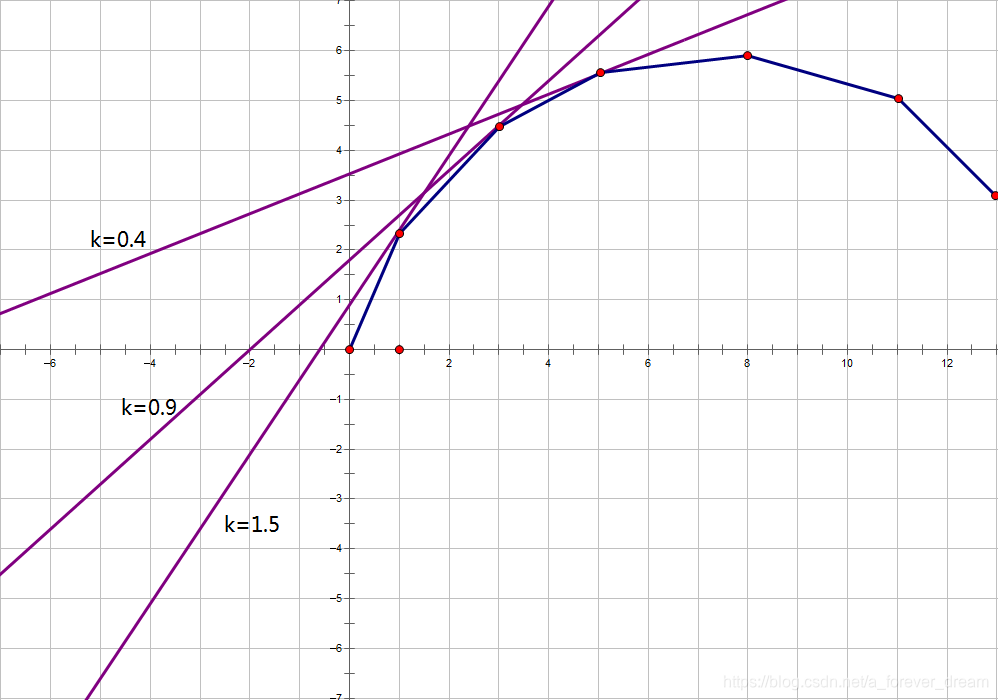
满足凸性就可以 wqs二分了。
算法
二分一个斜率 \(k\),一会儿就知道有什么用了。
我们让这个斜率为 \(k\) 的直线去切凸包。
我们现在要知道切的点 \(x\) 和 \(g(x)\) 是什么,这样就能不断调整 \(k\),直到我们的 \(k\) 切到我们要求的限制 \(m\),同时我们也能知道答案 \(g(m)\)。
注意我们并不是用 \(x\) 去求 \(g(x)\)。
我们看被切到的点满足什么性质。
发现斜率为 \(k\) 的直线经过它时的截距 \(b\) 最大。
就像这样:
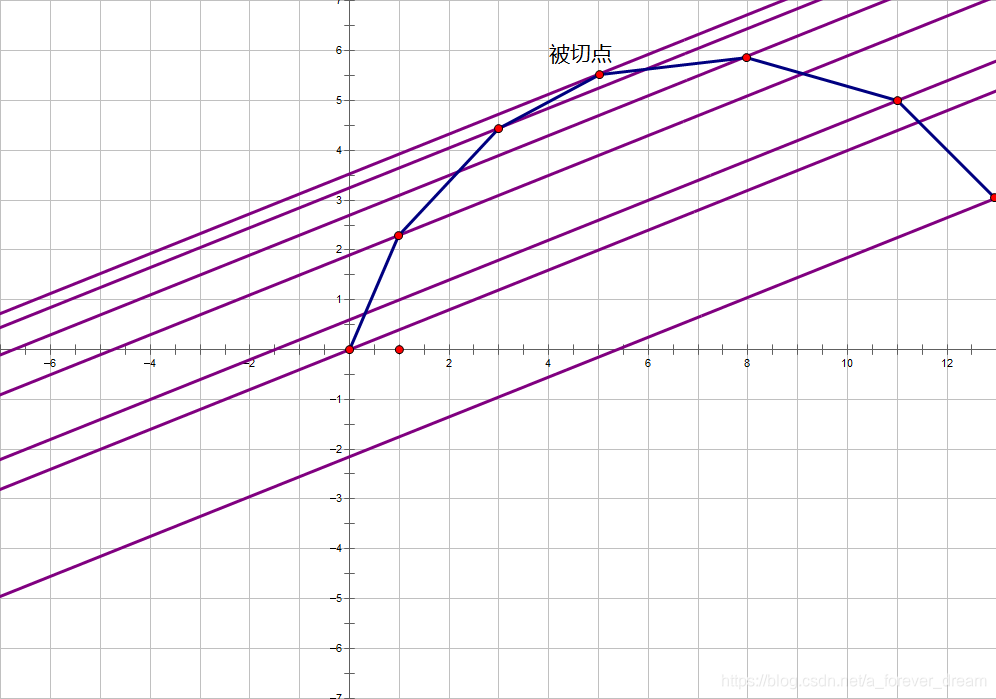
而我们又有,\(y=g(x)=kx+b\)。
即 \(b=g(x)-kx\),\(b\) 最大。
考虑 \(b\) 的意义:
在这里,我们的被切点 \(x\) 还没有确定。
所以对于任意 \(x\),我们取:使得 \(g(x)-kx\) 最大的 \(x\),这个 \(x\) 就是被切点。
由于 \(x\) 是任意的,所以 \(g(x)-kx\) 就相当于,我恰好选 \(x\) 个物品,每一个选的物品的价值都减少 \(k\)。
也可以看做所有物品价值都减少 \(k\),然后选恰好 \(x\) 个物品。
而对于任意 \(x\),取 \(g(x)-kx\) 最大的 \(x\)。就相当于每个物品价值减少 \(k\),可以选任意个物品,使得价值和 \(b\) 最大。
发现这就是文章开头说的没有限制选的物品个数的情况,这可以快速求。
于是我们就能知道我们选了多少个物品,选的个数为 \(x\),同时根据 \(g(x)=b+kx\) 知道我们的答案。
实现
从代码顺序的角度复述一遍上面所说的算法。
我们二分一个斜率 \(k\)。
此时把所有物品的价值减 \(k\),然后快速跑一遍:选任意个物品,价值和最大。
此时能得到选的物品个数 \(x\),与答案 \(b=g(x)-kx\)。
然后根据 \(x\) 调整斜率 \(k\)。
具体怎么调整?
根据 \(g(x)\) 的凸包的斜率单调性来调整即可。
二分,直到 \(x=m\),最后的答案就是 \(b+kx\)。
负优化 Trick:
当然你发现,当 \(x\ne m\) 时,答案或许没有用,我们可以跑到最后 \(x=m\) 时,再次用这个 \(k\) 跑一次求答案,当然这或许多此一举了。
优化费用流模型
wqs二分 常用于优化费用流模型,即优化反悔贪心&模拟费用流(反悔贪心就是模拟了费用流的退流操作)。
为什么可以优化?
因为费用流的费用是关于流量的凸函数。
例题
例题题解
需要注意的是,以下有一些关于 wqs 二分实现上的细节。
P2619 Tree I
我们再回顾一下 wqs 二分的过程,首先这道题目要解决的就是限定白边要恰好选 \(need\) 条,我们猜想(或感性理解)答案是关于白边边权的偏移量的凸函数,于是我们可以用 wqs 二分。
也就是二分一个偏移量,然后将白边边权都加上偏移量,然后求最小生成树,此时就能同时得到选择的白边数量和此时的权值和,然后再根据白边数量调整偏移量。
怎么调整呢,感性理解就是,加上的偏移量越小选的白边越多(因为是最小生成树).
这里,我们考虑用 Kruskal 求最小生成树,每次把白边加上偏移量,然后再排序。
实现细节:
-
首先偏移量为整数,然后范围为 \([-100,100]\),这恰好对应边权的范围。
-
注意到可能会出现这种情况:偏移量为 \(x\) 时选的白边数 \(<need\),而偏移量为 \(x-1\) 时,选的白边数 \(>need\),这该怎么办呢?
还有就是当排序时相等的白边和黑边优先选哪一条?
对于上面的问题,我们考虑为什么会出现这种情况,那就是当某条将要选的白边和将要选的黑边的权值相等时,我们不一定先选黑边也不一定先选白边。最后使得即使正确的偏移量也无法得到正确的白边数量。这种情况在凸函数的图像上就表现为出现了一段与 \(x\) 轴平行的线段,而答案在这条线段上。
怎么解决呢?我们可以优先选白边,也就是在排序时,遇到相等的白边和黑边时,优先把白边放到前面。设函数 \(check(Mid)\) 返回偏移量为 \(Mid\) 时选的白边数,然后我们在二分时将 \(check(Mid)\ge need\) 判定为合法条件即可(注意这道题保证了数据有解,若不保证则要先判断有无解再二分)。
-
我们可以把白边和黑边放在两个数组里,对于白边数组我们就加偏移量,然后用两个指针跑就可以将复杂度从 \(O(m\log m \log 200)\) 降为 \(O(m\log 200)\),注意依然要优先选择白边。
AC 代码(两个 \(\log\) 的每次再排序做法):
int n,m;
const int N=1e5+5;
struct arr{
int u,v,opt,co;
int dco;
void getread(){
read(u),read(v),read(dco),read(opt);
}
}a[N];
int fa[N];
int getfa(int x){
if(fa[x]==x)return x;
return fa[x]=getfa(fa[x]);
}
int sum;
int check(int x){
int cnt=0;
fo(i,1,m)if(!a[i].opt)a[i].co=a[i].dco-x;
else a[i].co=a[i].dco;
sort(a+1,a+1+m,[](auto x,auto y){
if(x.co==y.co)return x.opt<y.opt;
else return x.co<y.co;
});
sum=0;
fo(i,0,n-1)fa[i]=i;
fo(i,1,m){
int u=getfa(a[i].u),v=getfa(a[i].v);
if(u!=v){
fa[u]=v;
sum+=a[i].co;
if(a[i].opt==0)cnt++;
}
}
return cnt;
}
int ned;
signed main(){
// usefile("1");
read(n),read(m),read(ned);
fo(i,1,m){
a[i].getread();
}
int l=-101,r=101,ans=0;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid)>=ned)ans=mid,r=mid-1;
else l=mid+1;
}
check(ans);
write(sum+ans*ned);
return 0;
}
P5633 最小限度生成树
类似于上面这道题,然而由于可能无解,所以我们不能直接跑二分而需要先判断。
具体怎么判断有无解:
-
首先 \(s\) 的边的个数要 \(\ge k\)。
-
原图连通。
-
把 \(s\) 的边断掉,然后原图分成了很多连通块,连上 \(s\) 的至多 \(k\) 条边后原图连通,即连通块个数 \(\le k+1\)(包括 \(s\) 点的连通块)。
AC 代码:
int n,m,s,K;
const int N=5e5+5;
struct arr{
int u,v,w;
int opt;
int dw;
void Read(){
read(u),read(v),read(dw);
}
}a[N];
int fa[N];
int getfa(int x){
if(fa[x]==x)return x;
return fa[x]=getfa(fa[x]);
}
int sum;
int check(int x){
int cnt=0;
fo(i,1,m){
if(a[i].opt)a[i].w=a[i].dw+x;
else a[i].w=a[i].dw;
}
sort(a+1,a+1+m,[](auto x,auto y){
if(x.w==y.w)return x.opt>y.opt;
return x.w<y.w;
});
sum=0;
fo(i,1,n)fa[i]=i;
fo(i,1,m){
int u=getfa(a[i].u),v=getfa(a[i].v);
if(u!=v){
fa[u]=v;
sum+=a[i].w;
cnt+=a[i].opt;
}
}
return cnt;
}
signed main(){
// usefile("1");
read(n),read(m),read(s),read(K);
int Cnt=0;
int Flag=0;
fo(i,1,n)fa[i]=i;
fo(i,1,m){
a[i].Read();
if(a[i].u==s||a[i].v==s)a[i].opt=1,++Cnt;
else{
int u=getfa(a[i].u),v=getfa(a[i].v);
if(u!=v)fa[u]=v;
}
}
fo(i,1,n)if(getfa(i)==i)Flag++;
if(Flag<=K+1)Flag=1;
else Flag=0;
int L=-3e4-1,R=3e4+1,ans=0;
while(L<=R){
int mid=(L+R)>>1;
if(check(mid)>=K)ans=mid,L=mid+1;
else R=mid-1;
}
if(check(ans)>=K&&Cnt>=K&&Flag){
check(ans);
write(sum-ans*K);
}
else write("Impossible");
return 0;
}
jzoj 8118 coffee
题目大意
有 \(n\) 天的咖啡,第 \(i\) 天的咖啡价格 \(a_i\)。
有 \(m\) 张优惠券,每张优惠券可以在第 \(r_i\) 及之前的天使用,可以使一杯咖啡减少 \(w_i\)。
咖啡价格可以为负数,每天最多买一杯咖啡,每杯咖啡最多使用一张优惠券。
问买恰好 \(k\) 杯咖啡的最小价格。
数据范围:\(10^5\) 级别。
分析 & 解法
考虑没有 \(k\) 的限制时怎么做,这是经典的兔子进洞模型,考虑反悔贪心(模拟费用流)。
那么就是当某一杯咖啡使用优惠券后价格为负时就选它。
先插入 \(n\) 张 \(r=n,w=0\) 的优惠券,这对答案没有影响。
接下来将优惠券按 \(r_i\) 排序。
枚举优惠券,把在 \(r_i\) 之前的咖啡插入堆里。
每次取出堆顶的 \(x\),看是否为负,是则贡献为 \(x-w_i\)。
但是有个问题,就是后面可能还有 \(w_j\) 跟 \(x\) 配对更优,但是这个 \(w_i\) 已经把 \(x\) 的位置占掉了。
于是考虑反悔贪心的操作,即模拟费用流退流的操作。
我们在配对 \(x\) 与 \(w_i\) 后,往堆里再插入一杯价值为 \(w_i\) 的咖啡,这样后面再有 \(w_j\) 配对 \(x\) 时,它就要跟 \(w_i\) 配对,此时的贡献和为:
于是这是正确的。
有 \(k\) 的限制怎么办?
发现答案随 \(k\) 的增大具有凸性,考虑 wqs二分。
看看时间复杂度,有一个二分斜率的 \(\log\),还有一个堆的 \(\log\),总复杂度 \(O((m+n)\log^2 n)\)。
Raper
依然是反悔贪心,还是要注意 Tree I 中的细节问题。
邮局 加强版 加强版
这道题是四边形不等式得到决策单调性 DP,然后用 wqs 二分去掉个数的限制。
注意细节问题:
我们对于多个合法的决策点,我们优先选择下标小的,即在二分队列里我们用 \(<\) 判断优而不是用 \(\le\) 判断优,这样就能使对于同样的答案,我们选择的个数尽可能小,然后在比较时采用 \(check(mid)\le need\) 的做法。
而且我们发现多余的邮局可以舍去,所以不用判断二分是否有解的问题,同时运用 \(check(mid)\le need\) 刚好满足这个性质。
另外,输出答案应为 \(f_n-m*ans\) 而不是 \(f_n-cnt_n*ans\)。
这里就涉及到 wqs 二分的本质,我们二分的是斜率,然而二分的这个斜率可能切了很多个点,这个斜率得到的是截距,而我们的答案是截距加偏移量乘要求选的个数,因此我们得到的 \(cnt_n\) 不等于 \(m\) 时答案取后者就不对了。
也可以说,这几个点都可以被这个斜率的直线所切,截距都相等,然而我们求的答案与 \(m\) 即横坐标有关,而与 \(cnt\) 无关即横坐标不为 \(cnt\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号