最小生成树问题（Kruskal 算法）（克鲁斯卡尔）

  

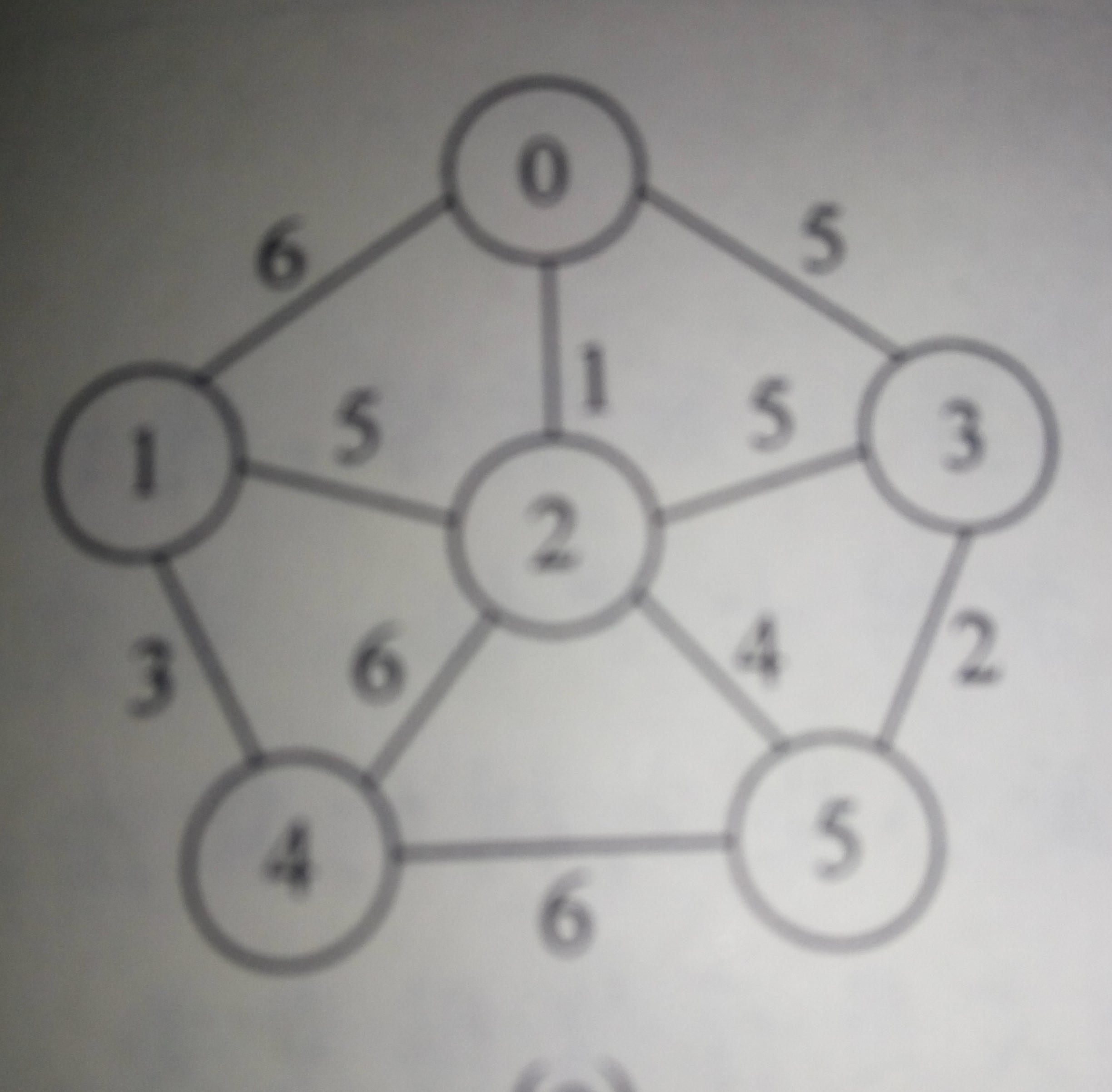
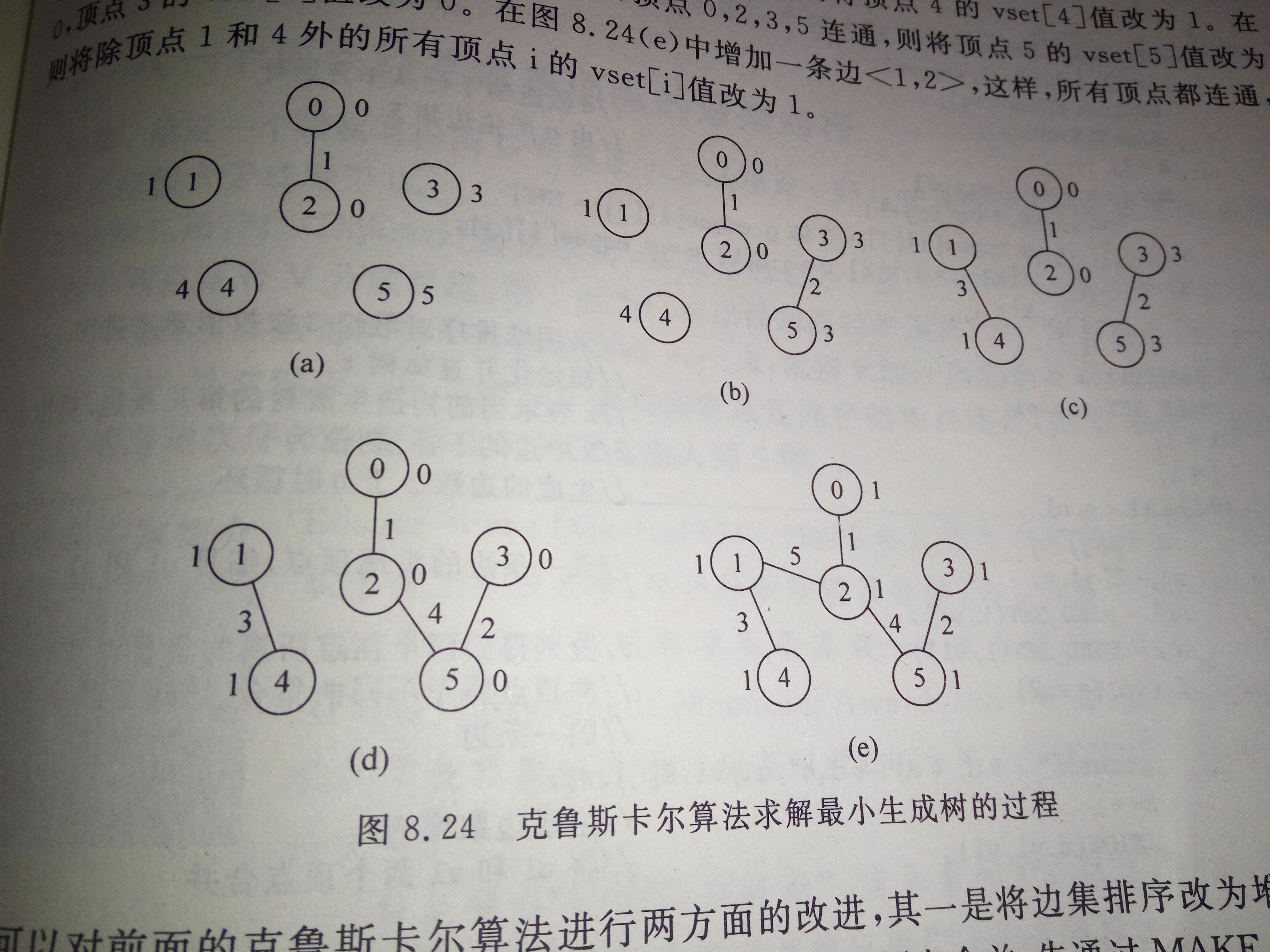
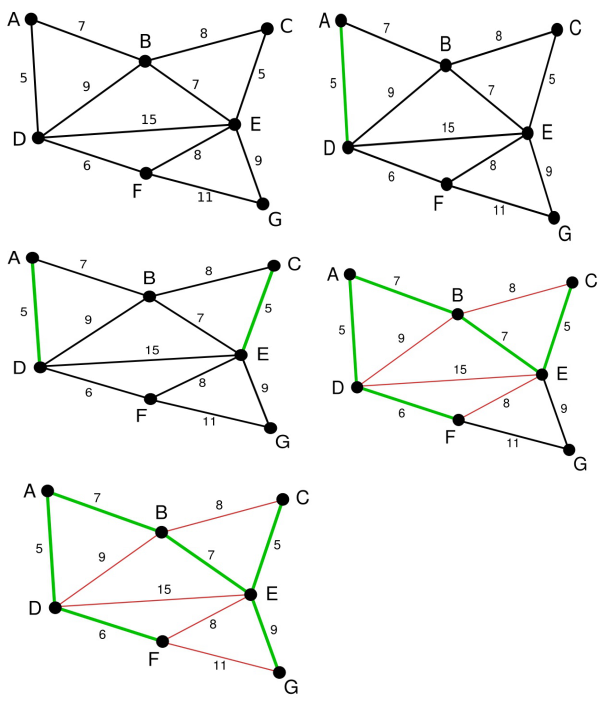
如图就是Kuskal算法

将图中的每条边按照权值从小到大排序，每次加起来就行，注意的是不要形成回路；

重点是如何用代码实现不能形成回路

看代码;

#include <cstdio>

#include <cstdlib>

#include <cstring>

#include <cmath>

#include <iostream>

#include <algorithm>

#define MaxSize 100

using namespace std;

int tu[MaxSize][MaxSize];

struct Edge//储存边的两个顶点以及边的权值

{

    int begin1;

    int end1;

    int weight;

};

bool comp(Edge a,Edge b)

{

    return a.weight<b.weight;

}

void Kruskal(int n)

{

    int vest[MaxSize];

    Edge E[MaxSize];

    int k=0;

    for(int i=1;i<=n;i++)

  for(int j=1;j<=n;j++)

        if(tu[i][j]!=0)

    {

        E[k].begin1=i;//将这条边的一个顶点储存

        E[k].end1=j;//将这条边的另一个顶点储存

        E[k].weight=tu[i][j];//将边的权值储存

        k++;//边的个数

    }

    sort(E,E+k,comp);//按照边的权值从大到小排序

    for(int i=0;i<=n;i++)

        vest[i]=i;//重点：将每个顶点初始化，看作是各不相同的集合

    k=1;

    int j=1,u1,v1,sn1,sn2;

    int sum=0;

    while(k<n)

    {

        u1=E[j].begin1;

        v1=E[j].end1;

        sn1=vest[u1];

        sn2=vest[v1]；//此条边的两个点

        if( sn1!=sn2)//两个点不属于一个集合

        {

 

            k++;

           sum+=E[j].weight;

            printf("< %d  ,  %d >:   %d      sum=%d\n", u1-1,v1-1,E[j].weight,sum);

           for(int i=1;i<=n;i++)

                if(vest[i]==sn2)

                vest[i]=sn1;//将找过的边的顶点都赋予相同的值，代表在一个集合内，此段代码将所有连在一起的顶点都标志成一个相同的值即                           vest[顶点编号]都是相同的；

        }

        j++;//遍历下一条边

    }

}

int  main()

{

    int n;

    scanf("%d",&n);

for(int i=1;i<=n;i++)

    for(int j=1;j<=n;j++)

    scanf("%d",&tu[i][j]);

    Kruskal(n);

 

    return 0;

}

/*

6

0 6 1 5 9999 9999

6 0 5 9999 3 9999

1 5 0 5 6 4

5 9999 5 0 9999 2

9999 3 6 9999 0 6

9999 9999 4 2 6 0

 

 

*/