数据结构:五 串
1. 串的定义
串(string)是由零个或多个字符组成的有限序列,又叫字符串
一般记为 s = "a1a2······an"(n>=0)
串中的字符数目 n 称为串的长度
零个字符的串称为空串(null string)
空格串:只包含空格的串,有内容有长度
子串:串中任意个数的连续字符组成的子序列,其位置是子串的第一个字符在主串中的序号
2. 串的比较
给定两个串:s = "a1a2······an",t = "b1b2······bm",满足以下条件之一时 s < t
- n < m,且 ai = bi(i = 1,2,··· ,n)
- 存在某个 k<= min(m, n) ,使得 ai = bi( i= 1,2,··· ,k - 1),ak < bk
3. 串的抽象数据类型
ADT 串(string)
Data 串中元素仅由一个字符组成,相邻元素具有前驱和后继关系
Operation StrAssign(T,*chars):生成一个其值等于字符串常量chars的串T。 StrCopy(T,S):串S存在,由串S复制得串T。 ClearString(S):串S存在,将串清空。 StringEmpty(S):若串为空,则返回true,否则返回false。 StrLength(S):返回S的元素个数,即串S的长度。 StrCompare(S,T):若S>T,返回>0,S=T,返回=0,S<T,返回<0. Concat(T,S1,S2):用T返回由S1和S2联接而成的新串。 SubString(Sub,S,pos,len):串S存在,1<=pos<=Strlength(S), 且0<=len<=Strlength(S)-pos+1. 用Sub返回串S的第pos个字符起长 度为len的子串。 Index(S,T,pos):串S和T存在,T是非空串,1<=pos<=Strlength(S). 若主串S中存在和串T值相同的字串,则返回它在主 串S中第pos个字符之后第一次出现的位置,否则返回0 Replace(S,T,V):串S,T和V存在,T是非空串。用V替换主串S中出现 的所有与T相等的不重叠的子串。 StrInsert(S,pos,T):串S和T存在,1<=pos<=Strlength(S)+1.
在串S的第pos个字符之前插入串T。 SteDelete(S,pos,len):串S存在,1<=pos<=StrLength(s)-len+1.
从串S中删除第pos个字符起长度为len的子串。 endADT
4. 串的存储结构
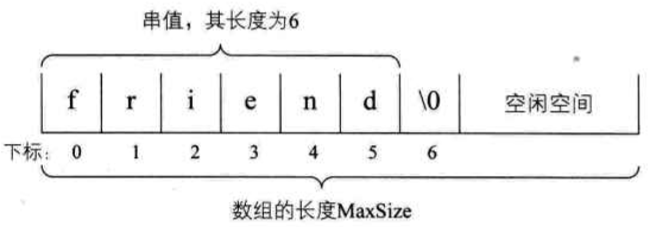
串的顺序存储结构
- 用一组地址连续的存储单元来存储串中的字符序列的
![]()
串的链式存储结构
- 一个结点可以存放一个字符,也可以考虑存放多个字符,最后一个结点若是未被占满时,可以用 “#” 或其它非串值字符补全
![]()
5. 朴素的模式匹配算法
子串的定位操作通常称作串的模式匹配
对主串的每一个字符作为子串开头,与要匹配的字符串进行匹配。对主串做大循环,每个字符开头做 T 的长度的小循环,直到匹配成功或全部遍历完成为止
最好情况
- 一开始就匹配成功,如 "googlegood" 中找 "google"
- 时间复杂度为:O(1)
一般情况
- 每次都是首字母就不匹配,如 "abcgoogle" 中找 "google"
- 时间复杂度:O(n + m),n 为主串长度,m 为要匹配的子串长度
最坏情况
- 每次不匹配都发生在匹配串的最后一个字符上
- 如 "0000000001" 中找 "0001"
- 时间复杂度:(n - m + 1) * m
![]()
6. KMP 模式匹配算法
原理
- 主串 S = "abcdefgabcdex",子串 T = "abcdex"
- 前提:如果我们知道 T 串中首字符 "a" 与 T 中后面的字符均不相等
- 而 T 串的第二位的 "b" 与 S 串中第二位的 "b" 已经判断是相等的,则 T 串中首字母 ”a“ 与 S 串中的第二位 "b" 是不需要判断也知道是不相等的

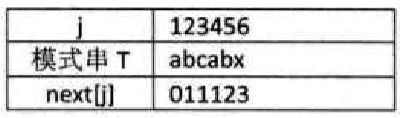
next 数组
- 我们把 T 串各个位置的 j 值的变化定义为一个数组 next,那么 next 的长度就是 T 串的长度
![]()
next 数组值推导
-
例一:T = "abcdex"
-
![]()
- 1)当 j=1 时,next[1]=0;
- 2)当 j=2 时,j 由 1 到 j-1 就只有字符 "a",属于其他情况 next[2]=1;
- 3)当 j=3 时,j 由 1 到 j-1 串是 "ab",显然 "a" 和 "b" 不相等,属于其他情况,next[3] = 1;
- 4)以后同理,所以最终此 T 串的 next[j] 为 011111
-
例二:T = "abcabx"
-
![]()
- 1)当 j=1 时,next[1]=0;
- 2)当 j=2 时,同上例说明,next[2]=1;
- 3)当 j=3 时,同上,next[3] = 1;
- 4)当 j=4 时,同上,next[4] = 1;
- 5)当 j=5 时,此时 j 由 1 到 j-1 的串是 "abca",前缀字符 "a" 与后缀字符 "a" 相等,因此可推算出 k 值为 2,因此 next[5]=2;
- 6)当 j=6 时,j 由 1 到 j-1 的串是 "abcab",由于前缀字符 "ab" 与后缀字符 "ab" 相等,所以 next[3]=3;
- 经验得出:如果前后缀一个字符相等,k 值是 2,两个字符 k 值是 3,n 个相等 k 值就是 n+1
-
例三:T = "ababaaaba"
-
![]()
- 1)当 j=1 时,next[1]=0;
- 2)当 j=2 时,同上,next[2]=1;
- 3)当 j=3 时,同上,next[3] = 1;
- 4)当 j=4 时,j 由 1 到 j-1 的串是 "aba",由于前缀字符 "a" 与后缀字符 "ab" 相等,所以 next[4]=2;
- 5)当 j=5 时,j 由 1 到 j-1 的串是 "abab",由于前缀字符 "ab" 与后缀字符 "ab" 相等,所以 next[5]=3;
- 6)当 j=6 时,j 由 1 到 j-1 的串是 "ababa",由于前缀字符 "aba" 与后缀字符 "aba" 相等,所以 next[6]=4;
- 7)当 j=7 时,j 由 1 到 j-1 的串是 "ababaa",由于前缀字符 "ab" 与后缀字符 "aa" 不相等,只有 "a" 相等,所以 next[7]=2;
- 8)当 j=8 时,j 由 1 到 j-1 的串是 "ababaaa",只有 "a" 相等,所以 next[8]=2;
- 9)当 j=9 时,j 由 1 到 j-1 的串是 "ababaaab",由于前缀字符 "ab" 与后缀字符 "ab" 相等,所以 next[9]=3;
-
例四:T = "aaaaaaaab"
-
![]()
- 1)当 j=1 时,next[1]=0;
- 2)当 j=2 时,同上,next[2]=1;
- 3)当 j=3 时,j 由 1 到 j-1 的串是 "aa",由于前缀字符 "a" 与后缀字符 "a" 相等,所以 next[3]=2;
- 4)当 j=4 时,j 由 1 到 j-1 的串是 "aaa",由于前缀字符 "aa" 与后缀字符 "aa" 相等,所以 next[4]=3;
- 5)......
- 6)当 j=9 时,j 由 1 到 j-1 的串是 "aaaaaaaa",由于前缀字符 "aaaaaaaa" 与后缀字符 "aaaaaaa" 相等,所以 next[9]=8;
KMP 模式匹配算法实现
KMP 模式匹配算法实现改进
-
缺陷
- 主串 S = "aaaabcde",子串 T = "aaaaax",其 next 数组值分别为 012345
- 当 i=5,j=5 时,"b" 与 "a" 不相等,因此 j=next[5]=4,此时 "b" 与 第 4 位置的 "a" 依旧不等
- 依次往后,直到 j=next[1]=0时,根据算法,此时i++,j++,得到 i=6,j=1
- 出现多余的判断
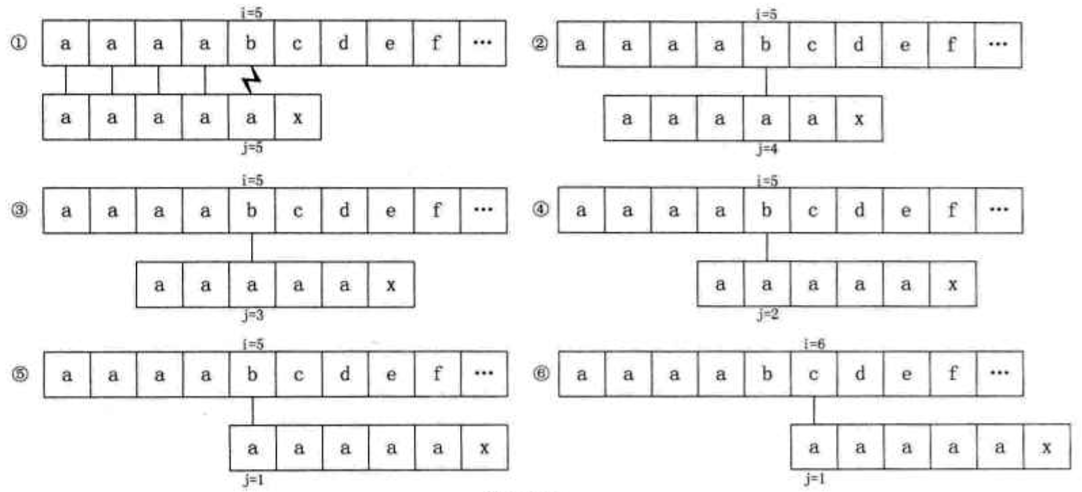
-
优化办法
- 由于 T 串的第二到五位置的字符都与首位的 "a" 相等,那么可以用首位 next[1] 的值去取代与它相等的字符后续 next[j] 的值
-
nextval 数组值推导
-
例:T = "ababaaaba"
-
![]()
- 先算出 next 数组的值分别为 001234223,然后再分别判断
- 1)当 j=1 时,nextval[1]=0;
- 2)当 j=2 时,因第二位字符 "b" 的 next 值是 1,而第一位就是 "a",它们不相等,所以 nextval[2] = next[2] = 1,维持原值;
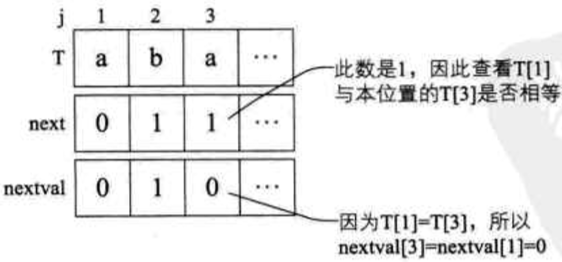
- 3)当 j=3 时,因第三位字符 "a" 的 next 值是 1,而第一位就是 "a",它们相等,所以 nextval[3] = nextval[1] = 0;
![]()
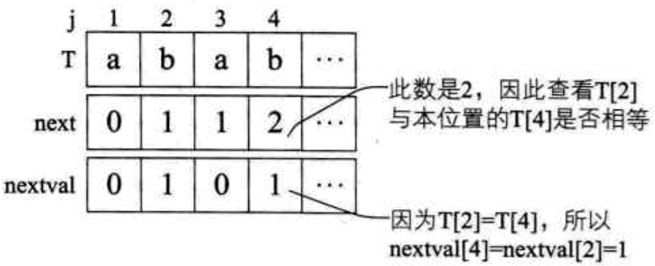
- 4)当 j=4 时,因第四位字符 "b" 的 next 值是 2,所以与第二位的 "b",它们相等,所以 nextval[4] = nextval[2] = 1;
![]()
- 5)当 j=5 时,next 值是 3,第五个字符 "a" 与第三个字符 "a" 相等,所以 nextval[5] = nextval[3] = 0;
- 6)当 j=6 时,next 值是 4,第六个字符 "a" 与第四个字符 "b" 不相等,所以 nextval[6] = 4;
- 7)当 j=7 时,next 值是 2,第七个字符 "a" 与第二个字符 "b" 不相等,所以 nextval[7] = 2;
- 8)当 j=8 时,next 值是 2,第八个字符 "b" 与第二个字符 "b" 相等,所以 nextval[8] = nextval[2] = 1;
- 9)当 j=9 时,next 值是 3,第九个字符 "a" 与第三个字符 "a" 相等,所以 nextval[9] = nextval[3] = 0;*
-
总结改进过的 KMP 算法
- 它是在计算出 next 值的同时,如果 a 位字符与它 next 值指向的 b 位字符相等,则该 a 位的 nextval 就指向 b 位的 nextval 值
- 如果不等,则该 a 位的 nextval 值就是它自己 a 位的 next 的值
-
从现在开始,种下梦想中的参天大树









 浙公网安备 33010602011771号
浙公网安备 33010602011771号