一、ROC曲线
1、简介
ROC曲线全称是“受试者工作特征曲线 ”(Receiver Operating Characteristic curve)，又称为感受性曲线(Sensitivity curve)。
它源于二战中用于敌机检测的雷达信号分析技术，二十世纪六七十年代开始被用于一些心理学、医学检测中，此后被引入机器学习领域。
得此名的原因在于曲线上各点反映着相同的感受性，它们都是对同一信号刺激的反应，只不过是在两种不同的判定标准下所得的结果而已。
ROC曲线示意图如下图所示。
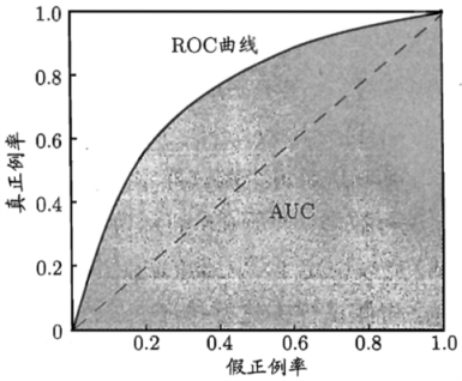
ROC曲线的横轴是“假正例率”（False Positive Rate，简称FPR），纵轴是“真正例率”（True Positive Rate，简称TPR），两者定义如下，公式中符号含义参见 混淆矩阵 。
\begin{align}\notag
TPR=\frac{TP}{TP+FN}
\end{align}
\begin{align}\notag
FPR=\frac{FP}{TN+FP}
\end{align}
现实任务中通常是利用有限个样本来绘制ROC曲线，此时仅能获得有限个（真正例率、假正例率）坐标，无法产生上图光滑的ROC曲线，只能绘制出下图所示的近似的ROC曲线。
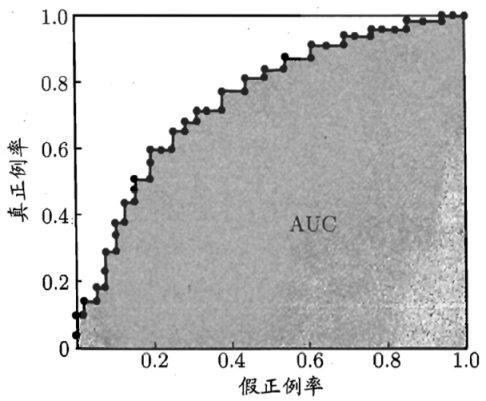
2、绘制方法
很多机器学习是为测试样本产生一个实值或概率预测，然后将这个预测值与一个分类阈值（threshold）进行比较，若大于阈值则分为正类，小于阈值则为反类。
- 假设有m个正例和n个反例，根据预测结果对样例进行排序；
- 把分类阈值设为最大，即把所有样例均预测为反例，此时真正例率和假正例率均为0，即在坐标（0，0）处；
- 然后，将分类阈值依次设为每个样例的预测值，即依次将每个样例划分为正例，求出真正例率和假正例率，绘制出坐标。
3.优点
在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。
但当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。
二、AUC
AUC（Area Under Curve），即ROC曲线下的面积。
AUC越大，分类器效果越好。
假设按序连接成ROC曲线上点的坐标为
\begin{align}\notag (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m}) \end{align}
则AUC可估算为\begin{align}\notag AUC=\frac{1}{2} \sum_{i=1}^{m-1}(x_{i+1}-x_{i})\cdot (y_{i}+y_{i+1}) \end{align}
梦不会逃走，逃走的一直都是自己。——《蜡笔小新》
