树状数组(BIT)

引入

给定一个长度为 \(n\) 的数列，\(A_1，A_2，…，A_{n-1}，A{n}\)，支持以下两种操作

1. \(add(x, y)\) 使得 \(A_x\)的值加上 \(y\)

2. \(query(x)\) 求得 \(\Sigma_{i=1}^{x} A_i\)的值

如果只有操作 2 的话, 大多数人都能立即想到使用 前缀和 求解, 但这里多了一个操作一, 使得前缀和无法继续使用. 在这里, 我们提出了树状数组.

树状数组(Binary Indexed Tree)

将原数列转化为下图形式

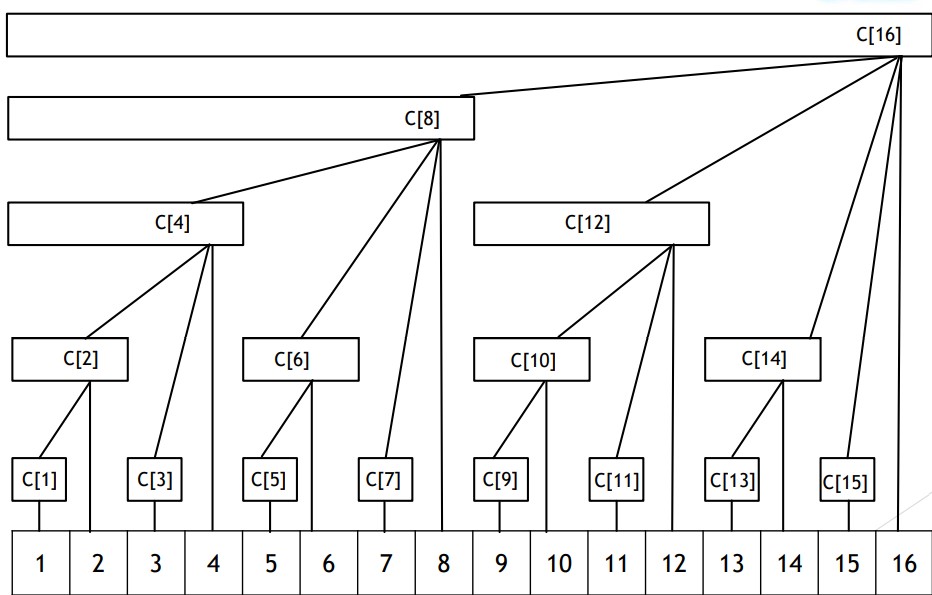
有以下性质存在:

• 每个内部节点\(c[x]\)保存以它为根的子树中所有叶子节点的和

• 每个内部节点\(c[x]\)的子节点个数等于\(lowbit(x)\)的位数

• 给个内部节点\(c[x]\)的子节点个数等于\(lowbit(x)\)的位数

• 树的深度是\(log(n)\)

什么是lowbit? 我的一篇blog中有解释: 点击访问

而 \(c_x = \Sigma_{i=x-lowbit(x)+1}^{x} a_{i}\)

(上面的式子和这个是一样的, 感觉不用 Σ 看的还清楚一点( :\(c_i=a_{i-lowbit(i)+1}+a_{i-lowbit(i)+2}+…+A_i\))

并可得出 \(query(x)\)可用以下代码求解

inline int query(int x) {
	int ans = 0;
	while (x > 0)
		ans += c[x], x -= lowbit(x);
	return ans;
}

举计算 \(\Sigma_{i=1}^7 a_i\) 的例子来证明:

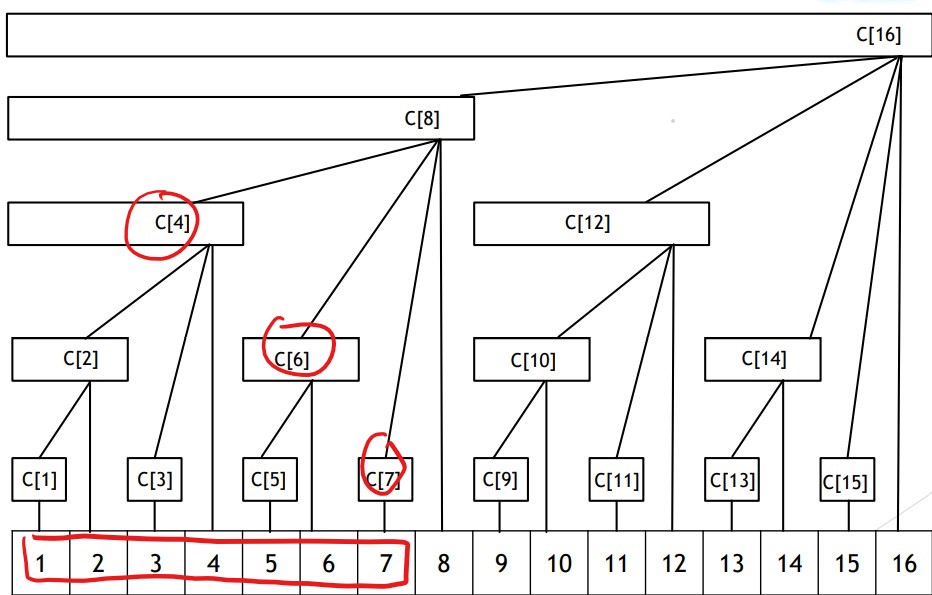
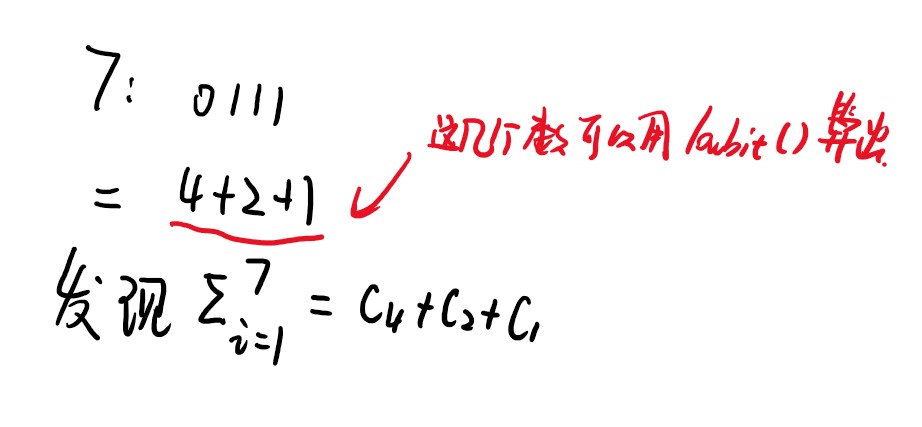
\(add(x, y)\) 可用以下代码求解

inline void add(int x, int y) {
	while (x <= n)
		c[x] += y, x += lowbit(x);
	return;
}

举 \(add(3, ...)\) 的例子说明

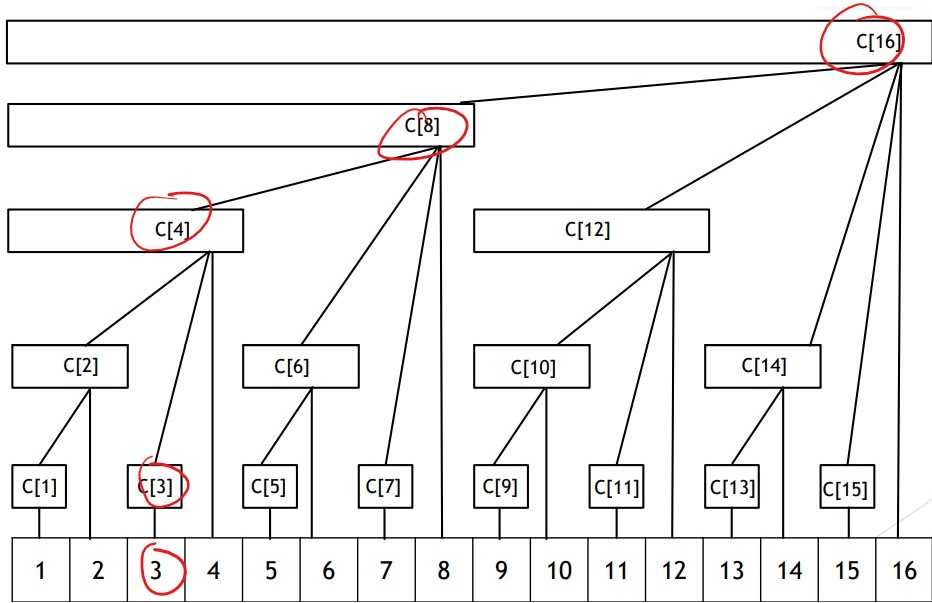
而初始化只需要和\(add(x, y)\)的过程其实就是一样的了

inline void init() {
	for (int i = 1; i <= n; i++)
		add(i, a[i]);
	return;
}

模板

#include <stdio.h>
#include <iostream>
using namespace std;
int n, m;
int a[500003], c[500003];
inline int lowbit(int x) {
	return x & (-x);
}
inline void add(int x, int y) {
	while (x <= n)
		c[x] += y, x += lowbit(x);
	return;
}
inline int query(int x) {
	int ans = 0;
	while (x > 0)
		ans += c[x], x -= lowbit(x);
	return ans;
}
inline void init() {
	for (int i = 1; i <= n; i++)
		add(i, a[i]);
	return;
}
int main() {
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++)
		scanf("%d", &a[i]);
	init();
	for (int i = 1; i <= m; i++) {
		int x, a, b;
		scanf("%d %d %d", &x, &a, &b);
		if (x == 1) 
			add(a, b);
		else
			printf("%d\n", query(b) - query(a-1));
	}
	return 0;
}

同时, 光记住模板是不够的, 我们要学会变通, 比如洛谷的P3368 【模板】树状数组 2, 与上面的代码只有两三行的区别, 却需要结合差分算法.

贴出 P3368 的代码

#include <stdio.h>
#include <iostream>
using namespace std;
int n, m;
int a[500003], c[500003];
inline int lowbit(int x) {
	return x & (-x);
}
inline int query(int x) {
	int ans = 0;
	while (x)
		ans += c[x], x -= lowbit(x);
	return ans;
}
inline void add(int x, int y) {
	while (x <= n)
		c[x] += y, x += lowbit(x);
	return;
}
inline void init() {
	for (int i = 1; i <= n; i++)
		add(i, a[i] - a[i-1]);		// 这里有改动(差分) 
	return;
}
int main() {
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++)
		scanf("%d", &a[i]);
	init();
/*	for (int i = 1; i <= n; i++)		// 删去注释查看输出可以发现, 此时的 query(i) = a[i] 
		printf("#%d %d\n", i, query(i)); */
	for (int i = 1; i <= m; i++) {
		int k, a, b, c;
		scanf("%d %d", &k, &a);
		if (k == 1) {
			scanf("%d %d", &b, &c);
			add(a, c);
			add(b + 1, -c);		// 这里有改动(差分) 
		}
		else
			printf("%d\n", query(a)); 
	}
	return 0;
}