LCA(最近公共祖先)总结
先留个坑
我回来了(
什么是 LCA
对于有根树T的两个结点u、v,最近公共祖先LCA(u,v)表示一个结点x,满足x是u和v的祖先且x的深度尽可能大。在这里,一个节点也可以是它自己的祖先。
以上, 百度百科中的定义, 不仅是你, 我也看不懂.
简单点说, 就是一棵有根树中两个节点的最近公共祖先, 下面我还是画图举例说明.
这次用的是这个画的树, 感觉有点奇怪不过没办法了(
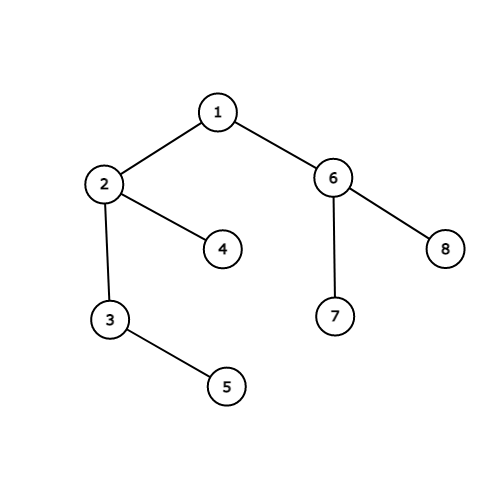
若上图中树根为1, 则有:
\(lca(3, 7)=1\)
\(lca(3, 2)=2\)
\(lca(3, 4)=2\)
等等
程序问题
tarjan 法
好处是速度更快, 时间复杂度\(O(n + m)\)
可以根据这篇blog中的图分析问题, 强烈建议带上纸笔跟着文字画一画.
思路讲一下:
首先保存每一个节点的父亲与儿子, 读取问题之后用 dfs 遍历的同时得出答案, 是一个离线算法.
P.S. 用到了并查集的思想.
我们初始化每个节点的父亲(fa[])为它自身, 当节点访问完后再更新他真正的父亲(树根的父亲是他自己). 对于每一个访问过的节点 \(i\), 如果 \(fa[i] = i\), 那么这个节点就没有访问完, 就一定是当前正在访问中的节点的祖先.
而在 dfs 搜索节点 cur 的时候, 我们需要做这些事:
- 遍历他所有的儿子.
- 查看有没有与当前节点有关的问题 \((cur, x)\), 如果有且 x 访问过, 我们便可以从 x 节点开始向上寻找第一个 \(fa[i] = i\) 的节点, 这个节点便是这 (cur, x) 的最近公共祖先.
- 更新节点 cur 的状态.
具体的还是看代码比较好吧(
#include <stdio.h>
#include <iostream>
#include <vector>
using namespace std;
int n, m, s;
int fa[500003];
int head[500003], next[1000003], val[1000003], cnt = 0;
struct NODE {
int x;
int id;
};
vector <NODE> q[500003];
int ans[500003];
bool vis[500003]; // 其实这东西似乎可以不要, 不过用了之后似乎会便于理解?
inline void add (int x, int y) {
val[++cnt] = y;
next[cnt] = head[x];
head[x] = cnt;
return;
}
inline void init () {
for (int i = 1; i <= n; i++)
fa[i] = i;
return;
}
inline int find (int x) { // 向上寻找
if (fa[x] != x)
return find(fa[x]);
return x;
}
inline void tarjan (int cur, int father) { // dfs
// 1. 访问所有儿子
for (int i = head[cur]; i; i = next[i]) {
int x = val[i];
if (x == father)
continue;
tarjan(x, cur);
}
// 2. 查看所有与当前节点有关系的问题并回答能回答的
for (int i = 0; i < q[cur].size(); i++) {
int x = q[cur][i].x;
if (vis[x])
ans[q[cur][i].id] = find(x);
}
// 3. 更新当前节点的信息
vis[cur] = true;
fa[cur] = cur == s ? s : father; // 注意 s (树根) 的父亲是他自己
return;
}
int main() {
scanf("%d %d %d", &n, &m, &s);
for (int i = 1; i < n; i++) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b);
add(b, a);
}
for (int i = 1; i <= m; i++) {
NODE nd;
nd.id = i;
int x, y;
scanf("%d %d", &x, &y);
nd.x = x, q[y].push_back(nd);
nd.x = y, q[x].push_back(nd);
}
init();
tarjan(s, 0);
for (int i = 1; i <= n; i++)
printf("%d\n", ans[i]);
return 0;
}
倍增法
慢一点, 但我觉得更好写一些.
直接贴源代码了, 不是很难, 注释(虽然只有核心代码写了一些)写的应该比较清楚, 实在不行看洛谷题解吧, 我懒得写了(
#include <stdio.h>
#include <iostream>
using namespace std;
int n, m, s;
int head[500003], val[1000003], last[1000003], cnt = 0;
int fa[500003][50], depth[500003];
int lg[500003];
inline void add(int x, int y) {
val[++cnt] = y;
last[cnt] = head[x];
head[x] = cnt;
return;
}
inline int lca(int x, int y) {
// 1. 使得较深的那个节点向上移, 直至两个节点高度相同
if (depth[x] < depth[y])
swap(x, y);
while (depth[x] > depth[y])
x = fa[x][lg[depth[x] - depth[y]] - 1];
// 2. 两个节点一起向上移, 直至两个节点重合
if (x == y) // 特判, 即 y 是 x 的祖先的情况
return x;
for (int k = lg[depth[y]] - 1; k >= 0; k--)
if (fa[x][k] != fa[y][k])
x = fa[x][k], y = fa[y][k];
return fa[x][0];
}
void dfs(int cur, int father, int high) { // 获取所有节点的祖先和深度
depth[cur] = high;
fa[cur][0] = father;
for (int i = 1; i <= lg[depth[cur]]; i++)
fa[cur][i] = fa[fa[cur][i-1]][i-1];
for (int i = head[cur]; i; i = last[i])
if (val[i] != father)
dfs(val[i], cur, high + 1);
return;
}
inline void init() {
for (int i = 1; i <= n; i++)
lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
return;
}
int main() {
scanf("%d %d %d", &n, &m, &s);
init();
for (int i = 1; i < n; i++) {
int x, y;
scanf("%d %d", &x, &y);
add(x, y); add(y, x);
}
dfs(s, 0, 1);
for (int i = 1; i <= m; i++) {
int x, y;
scanf("%d %d", &x, &y);
printf("%d\n", lca(x, y));
}
return 0;
}
咕咕咕 应该还有后续内容(例题), 等着吧(
例题 [BZOJ1832 [AHOI2008]聚会]
题目描述
Y岛风景美丽宜人,气候温和,物产丰富。
Y岛上有N个城市(编号1,2,…,N),有N-1条城市间的道路连接着它们。
每一条道路都连接某两个城市。
幸运的是,小可可通过这些道路可以走遍Y岛的所有城市。
神奇的是,乘车经过每条道路所需要的费用都是一样的。
小可可,小卡卡和小YY经常想聚会,每次聚会,他们都会选择一个城市,使得3个人到达这个城市的总费用最小。
由于他们计划中还会有很多次聚会,每次都选择一个地点是很烦人的事情,所以他们决定把这件事情交给你来完成。
他们会提供给你地图以及若干次聚会前他们所处的位置,希望你为他们的每一次聚会选择一个合适的地点。
输入格式
第一行两个正整数,N和M,分别表示城市个数和聚会次数。
后面有N-1行,每行用两个正整数A和B表示编号为A和编号为B的城市之间有一条路。
再后面有M行,每行用三个正整数表示一次聚会的情况:小可可所在的城市编号,小卡卡所在的城市编号以及小YY所在的城市编号。
输出格式
一共有M行,每行两个数Pos和Cost,用一个空格隔开,表示第i次聚会的地点选择在编号为Pos的城市,总共的费用是经过Cost条道路所花费的费用。
输入样例#1
6 4
1 2
2 3
2 4
4 5
5 6
4 5 6
6 3 1
2 4 4
6 6 6
输出样例#1
5 2
2 5
4 1
6 0
数据范围
N≤500000,M≤500000
可以画图, 发现三个节点的 lca 中至少有两个相同, 分类讨论:
- 三个都相同, 则他们的 lca 即为聚会地点
- 有两个相同, 令其为 x, 另一个为 y, 则 x 一定是最佳的聚会地点, 具体的话可以画图, 用一个类似于贪心的思想去证明
所以我们只需要求出三个节点中两两的 lca, 然后几个 if 判断即可, 距离的话加一个前缀和(深度)就可以了.
代码如下
#include <stdio.h>
#include <iostream>
using namespace std;
int n, m;
int head[500003], val[1000003], last[1000003], cnt = 0;
int fa[500003][50], depth[500003];
int lg[500003];
inline void add(int x, int y) {
val[++cnt] = y;
last[cnt] = head[x];
head[x] = cnt;
return;
}
inline int lca(int x, int y) {
if (depth[x] < depth[y])
swap(x, y);
while (depth[x] > depth[y])
x = fa[x][lg[depth[x] - depth[y]] - 1];
if (x == y)
return x;
for (int k = lg[depth[y]] - 1; k >= 0; k--)
if (fa[x][k] != fa[y][k])
x = fa[x][k], y = fa[y][k];
return fa[x][0];
}
void dfs(int cur, int father, int high) {
depth[cur] = high;
fa[cur][0] = father;
for (int i = 1; i <= lg[depth[cur]]; i++)
fa[cur][i] = fa[fa[cur][i-1]][i-1];
for (int i = head[cur]; i; i = last[i])
if (val[i] != father)
dfs(val[i], cur, high + 1);
return;
}
inline void init() {
for (int i = 1; i <= n; i++)
lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
return;
}
int main() {
scanf("%d %d", &n, &m);
init();
for (int i = 1; i < n; i++) {
int x, y;
scanf("%d %d", &x, &y);
add(x, y); add(y, x);
}
dfs(1, 0, 1);
for (int i = 1; i <= m; i++) {
int x, y, z;
scanf("%d %d %d", &x, &y, &z);
int lca1 = lca(x, y), lca2 = lca(y, z), lca3 = lca(z, x), ans;
if (lca1 == lca2)
ans = lca3;
else if(lca1 == lca3)
ans = lca2;
else
ans = lca1;
printf("%d %d\n", ans, depth[x] + depth[y] + depth[z] - depth[lca1] - depth[lca2] - depth[lca3]);
}
return 0;
}
咕咕咕, 后面还会有例题的.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号