OpenFoam——计算单元网格梯度（gradf）

计算流程如下：

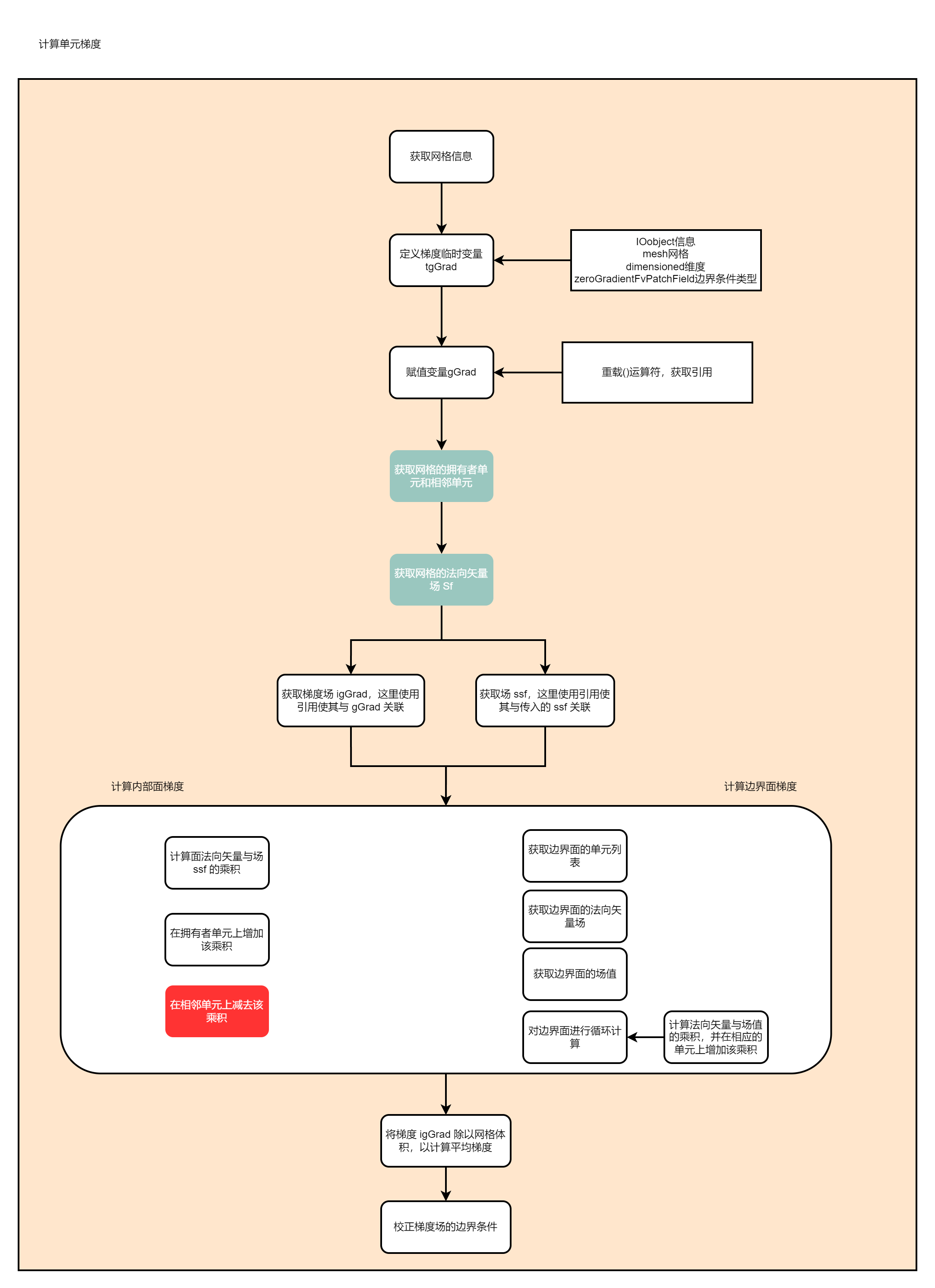
代码如下：

Foam::fv::gaussGrad<Type>::gradf
(
 const GeometricField<Type, fvsPatchField, surfaceMesh>& ssf,
 const word& name
)
{
	// 定义一个类型为 GradType 的类型别名，GradType 表示梯度场的类型
	typedef typename outerProduct<vector, Type>::type GradType;
	// 获取传入场 ssf 的网格信息
	const fvMesh& mesh = ssf.mesh();
	// 声明一个名为 tgGrad 的临时变量，类型为 GeometricField<GradType, fvPatchField, volMesh>
	// 使用 new 运算符创建一个 GeometricField 实例，并将其存储在 tgGrad 中
	// 新创建的 GeometricField 使用了给定的 name 和 mesh 作为 IOobject，表示它在磁盘上没有读写权限
	// dimensioned<GradType> 表示场的维度，初始化为零向量
	// zeroGradientFvPatchField<GradType>::typeName 表示边界条件类型，这里是零梯度条件
	tmp<GeometricField<GradType, fvPatchField, volMesh> > tgGrad
	(
		new GeometricField<GradType, fvPatchField, volMesh>
		(
			IOobject
			(
				name,
				ssf.instance(),
				mesh,
				IOobject::NO_READ,
				IOobject::NO_WRITE
			),
			mesh,
			dimensioned<GradType>
			(
				"0",
				ssf.dimensions()/dimLength,
				pTraits<GradType>::zero
			),
			zeroGradientFvPatchField<GradType>::typeName
		)
	);
	
	// 将 tgGrad 赋值给一个名为 gGrad 的变量，类型为 GeometricField<GradType, fvPatchField, volMesh>
	// 这里使用了括号运算符重载，使得 gGrad 成为对 tgGrad 的引用
	GeometricField<GradType, fvPatchField, volMesh>& gGrad = tgGrad();
	// 获取网格的拥有者单元和相邻单元
	const labelUList& owner = mesh.owner();
	const labelUList& neighbour = mesh.neighbour();
	// 获取网格的法向矢量场 Sf
	const vectorField& Sf = mesh.Sf();
	// 获取梯度场 igGrad，这里使用引用使其与 gGrad 关联
	Field<GradType>& igGrad = gGrad;
	// 获取场 ssf，这里使用引用使其与传入的 ssf 关联
	const Field<Type>& issf = ssf;
	// 计算内部面的梯度
	forAll(owner, facei)
	{
		// 计算面法向矢量与场 ssf 的乘积
		GradType Sfssf = Sf[facei]*issf[facei];
		// 在拥有者单元上增加该乘积
		igGrad[owner[facei]] += Sfssf;
		// 在相邻单元上减去该乘积
		igGrad[neighbour[facei]] -= Sfssf;
	}
	// 计算边界面的梯度
	forAll(mesh.boundary(), patchi)
	{
		// 获取边界面的单元列表
		const labelUList& pFaceCells = mesh.boundary()[patchi].faceCells();
		// 获取边界面的法向矢量场
		const vectorField& pSf = mesh.Sf().boundaryField()[patchi];
		// 获取边界面的场值
		const fvsPatchField<Type>& pssf = ssf.boundaryField()[patchi];
		// 对边界面进行循环计算
		forAll(mesh.boundary()[patchi], facei)
		{
			// 计算法向矢量与场值的乘积，并在相应的单元上增加该乘积
			igGrad[pFaceCells[facei]] += pSf[facei]*pssf[facei];
		}
	}
	// 将梯度 igGrad 除以网格体积，以计算平均梯度
	igGrad /= mesh.V();
	// 校正梯度场的边界条件
	gGrad.correctBoundaryConditions();
	// 返回校正后的梯度场 tgGrad
	return tgGrad;
}

红色部分：
在OpenFOAM中计算梯度时，在拥有者单元上增加面法向矢量与场 ssf 的乘积，同时在相邻单元上减去该乘积的目的是为了保证在计算梯度时满足散度定理（divergence theorem），以确保梯度场的散度为零。

考虑一个场 F 在二维情况下的散度，即 ∇·F。根据散度定理，在一个有界区域内，该场 F 的散度等于边界面上通过场 F 流出的通量。这意味着，在边界面上，通量的流出等于通量的流入。如果在计算梯度时，不考虑这种通量平衡，可能会导致梯度场的散度不为零，这是不符合物理规律的。

因此，在计算梯度时，OpenFOAM采用了通量平衡的方法，将面法向矢量与场 ssf 的乘积分别添加到拥有者单元和相邻单元上。这样，在边界面上通量的增减是平衡的，从而确保梯度场的散度为零，使得梯度计算结果更加准确和物理合理。