CFD——非结构网格梯度计算（不修正）

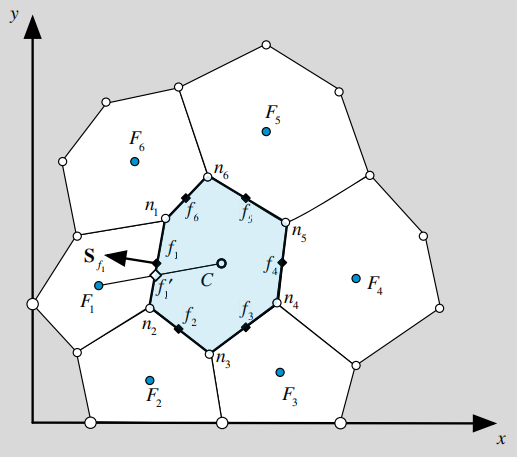
本案例在计算非结构网格的梯度时，不使用修正方法。将直接使用f'处的∅值

计算流程

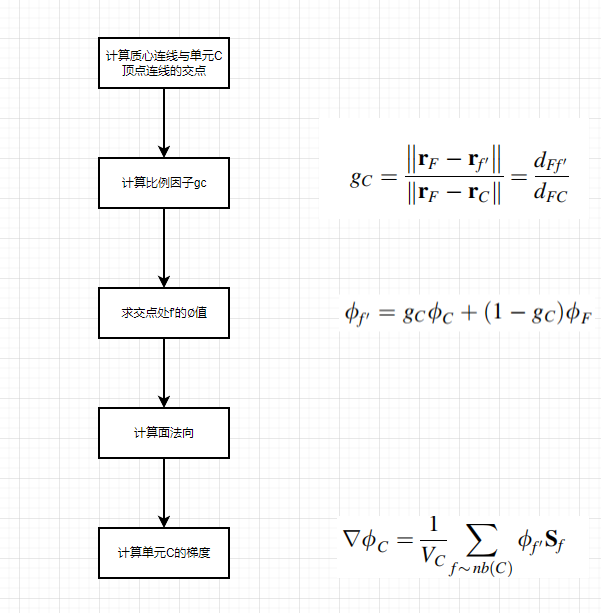
import numpy as np

N = 6

# 各质心的位置坐标
P_C = np.array([13,11])
P_F_List = np.array([[4.5,9.5],[8,3],[17,3.5],[22,10],[16,20],[7,18]])

# C单元各个顶点坐标
P_n_List = np.array([[9,14],[8,8],[12,5],[17,9],[17.5,14],[12,17]])

# 各单元值
phi_C = 167
phi_F_List =  np.array([56.75,35,80,252,356,151])

# 各单元的梯度
gra_phi_F_List = np.array([[10.5,5.5],[4,9],[4.5,18],[115,23],[21,17],[19,8]])

# C单元体积
V_C = 76

# C单元顶点连线nn矢量
nn_List = np.random.rand(N, 2)
for i in range(N):
  if i < 5:
    nn_List[i] = P_n_List[i+1] - P_n_List[i]
  else:
    nn_List[i] = P_n_List[0] - P_n_List[i]

# C单元与周围单元质心连线，CF矢量
CF_List = np.random.rand(N, 2)
for i in range(N):
  CF_List[i] = P_F_List[i] - P_C

# 计算两直线的交点函数
def intersection_point(point1, point2,point3,point4):
  n1n2 = point2 - point1
  CF1 = point4 - point3
  n1n2_k = n1n2[1]/n1n2[0]
  n1n2_b = point1[1] - n1n2_k * point1[0]
  CF1_k = CF1[1]/CF1[0]
  CF1_b = point3[1] - CF1_k * point3[0]
  x = (n1n2_b - CF1_b) / ( CF1_k - n1n2_k)
  y = n1n2_k * x + n1n2_b
  return np.array([x,y])

# 计算两点之间的距离
def distance_two_points(point1,point2):
  dis = ((point1[0]-point2[0])**2+(point1[0]-point2[0])**2)**0.5
  return dis

# 两直线的交点
P_nn_CF_List = np.random.rand(N, 2)
for i in range(N):
  if i < N-1:
    P_nn_CF_List[i] = intersection_point(P_n_List[i],P_n_List[i+1],P_C,P_F_List[i])
  else:
    P_nn_CF_List[i] = intersection_point(P_n_List[i],P_n_List[0],P_C,P_F_List[i])

# gc比例
gc_CF_List = np.random.rand(N)
for i in range(N):
  gc_CF_List[i] = distance_two_points(P_nn_CF_List[i],P_F_List[i])/distance_two_points(P_C,P_F_List[i])

# 顶点连线与质心连线交点的phi值
phi_f_sk_List = np.random.rand(N)
for i in range(N):
  phi_f_sk_List[i] = gc_CF_List[i] * phi_C + (1 - gc_CF_List[i]) * phi_F_List[i]

# 计算面法向
Sf_List = np.random.rand(N, 2)
for i in range(N):
  Sf_List[i][0] = nn_List[i][1]
  Sf_List[i][1] = -nn_List[i][0]

print(Sf_List)
print(phi_f_sk_List)

# 计算单元C的梯度，gra_phi_C
gra_phi_C = np.random.rand(2)
sumi = 0
sumj = 0
for i in range(N):
  sumi += phi_f_sk_List[i] * Sf_List[i][0]
  sumj += phi_f_sk_List[i] * Sf_List[i][1]
gra_phi_C[0] = sumi/V_C
gra_phi_C[1] = sumj/V_C