深入浅出图神经网络 第4章 表示学习 读书笔记

第4章 表示学习

在第2章的时候提到了机器学习的第一步就是提取特征。而表示学习就是自动地从数据中学习特征，并直接用于后续的任务。

4.1 表示学习

4.1.1 表示学习的意义

表示学习要回答3个问题：

1. 如何判断一个表示比另一个表示更好？
2. 如何挖掘这些表示？
3. 使用什么样的目标去得到一个好的表示？

举一个例子就是一个图像，计算机能够得到的知识一个个像素点这样的原始数据，只关注像素点是无法得到一些具体信息的；而人在看到一个图像的时候自然会通过高层的抽象语义来判断。一个好的表示就应该尽可能提供高层次的有价值的特征。

4.1.2 离散表示与分布式表示

机器学习中对一个对象的表示有两种常见的方式：独热编码（one-hot）和分布式表示。

独热码就是表示成一个响亮，只在某个维度上为1，其余全为0。

分布式表示就是得到一个低维稠密的向量来表示研究对象，典型的例子就是颜色，可以用RGB值的三元组来表示。

独热码表示起来非常简单，但它会使得所有不同的表示都是相互独立（正交）的，这会让它表示起来丢失大量的语义信息。而分布式表示就能够保留这些语义信息，当然相应的也会比独热码实现起来更复杂一点。

4.1.3 端到端学习

所谓端到端学习就是以原始输入作为输入，并直接输出想要得到结果（比如分类）。相应的，传统的机器学习模型中，一些工作都是先处理输入，通过特征工程提取出特征，之后再交由分类器进行判断。

由此端到端学习可以看作是表示学习与任务学习的结合（提取特征+分类），它们不是完全分裂的，而是联合优化的，一次反向传播更新的不只是基于特征给出分类结果的参数，还更新了提取特征的参数使得整个模型的效果会更好，这体现了深度学习模型的优越性。

深度学习模型另一个优势是能够学习到数据的层次化表达。低层次的特征更加通用，高层次的特征则更贴近具体任务，所以对于一些比较相近的任务，其实是可以使用相同的低层次特征的，这让深度学习可以进行迁移学习。

4.2 自编码器：基于重构损失的方法

自编码器是一种无监督的学习模型，可以用于数据降维和特征提取。

4.2.1 自编码器

自编码器的思路是：将输入映射到某个特征空间，再从这个特征空间映射回输入空间进行重构。结构上看它由编码器和解码器组成，编码器用于从输入中提取特征，解码器则用于从特征重构出输入数据。

考虑一个最简单的自编码器：1个输入层、1个隐藏层、1个输出层。那么从输入到隐藏层就是编码器，从隐藏层到输出层就是解码器。

对于输入\(x\in R^n\)，输入层到隐藏层的变换矩阵为\(W_{enc}\in R^{n\times d}\)，\(d\)是隐藏层神经元数目，

经过变换\(h=\sigma(W_{enc}x+b_{enc})\)得到编码后的特征\(h\in R^d\)。

解码器将特征\(h\)映射回输入空间，隐藏层的输出层的变换矩阵为\(W_{dec}\in R^{d\times n}\)，经过变换\(\widetilde x=\sigma(W_{dec}h+b_{dec})\)得到重构的输入\(\widetilde x\)。

自编码器不需要标签进行监督学习，其是通过不断最小化输入和输出之间的重构误差来进行训练的，利用损失函数\(L=\frac{1}{N}\Sigma_i||x_i=\widetilde x_i||_2^2\)，通过反向传播计算梯度，再通过梯度下降优化\(W_{enc},W_{dec},b_{enc},b_{dec}\)。

一般来说编码器和解码器会用更复杂的模型，用函数\(f,g\)来表示，那么损失就变为\(L=\frac{1}{N}\Sigma_i||x_i=g(f(x_i))||_2^2\)。

关于这个判断\(x_i\)是否相等的二范数损失我有点不知道具体是怎么算的，稍微查了查资料没找到什么有用的，有朋友知道的话欢迎评论区指教！

比较容易混淆的一点是：这个自编码器先编码再解码，最后得到的不还是原始输入或者逼近原始输入的东西吗？所以要特别注意，自编码器训练完后，是直接拿输入过一个编码器进行特征提取再放到后面的神经网络里去的，解码器就用不到了，有种GAN的思想。

实际使用中，通常有\(d<n\)，因为要进行降维嘛，符合这种条件的编码器被称为欠完备自编码器。

4.2.2 正则自编码器

如果编码器的维度大于等于输入的维度\(d\ge n\)，那么就被称为过完备自编码器。如果不对过完备自编码器进行一些限制，那么其可能会更倾向于将输入拷贝到输出，从而得不到特征。因此通常会对模型进行一些正则化的约束。

去噪自编码器

去噪自编码器在原始输入的基础上加入了一些噪声作为输入，这使得解码器需要重构出不加入噪声的原始输入，这迫使编码器不能简单地进行一个恒等变换，而必须能够从含噪声的输入中提取出原始输入。

加入噪声的具体方法是随机将输入\(x\)中的一部分置为0，得到\(x_\delta\)作为输入，解码器则需要得到原始的输入\(x\)，那么有损失函数：\(L=\frac{1}{N}\Sigma_i||x=g(f(x_\delta))||^2_2\)。

稀疏自编码器

在损失函数上加入正则项使得模型学习到有用的特征，比如隐藏层使用Sigmoid激活函数，我们认为神经元的输出接近1时是活跃的，而接近0时是不活跃的，稀疏自编码器就是限制神经元的活跃度来约束模型，尽可能使大多数神经元处于不活跃的状态。

定义神经元的活跃度为它在所有样本上的平均值，用\(\hat\rho_i\)，限制\(\hat\rho_i=\rho_i\)，\(\rho_i\)是一个超参数，表示期望的活跃度，通常是接近于0的值。对偏离超参数较大的神经元进行惩罚就可以得到稀疏的编码特征，用相对熵作为正则项有\(L_{sparse}=\Sigma^d_{j=1}\rho log\frac{\rho}{\hat\rho_j}+(1-\rho)log\frac{1-\rho}{1-\hat\rho_j}\)。

相对熵可以量化表示两个概率分布之间的差异，当两个分布相差越大时相对熵值越大；两个分布完全相同时相对熵值为0。

最后的损失函数为\(L=L(x_i,g(f(x_i))+\lambda L_{sparse}\)，其中\(\lambda\)是调节重构项与稀疏正则项的权重。

4.2.3 变分自编码器

变分自编码器可以用于生成新的样本数据。

变分自编码器的原理

变分自编码器的本质是生成模型，其假设样本都是服从某个分布\(P(x)\)，通过建模\(P(X)\)，就可以从分布中进行采样得到新的样本数据。

一般来说每个样本都可能受到一些因素的控制，称为隐变量。假设有多个隐变量，用向量\(z\)表示，概率密度函数为\(p(z)\)。同时有一个函数\(f(z:\theta)\)可以吧\(p(z)\)中采样的数据\(z\)映射为与\(X\)比较相似的数据样本，即\(p(X|z)\)的概率更高。

（再后续的介绍超级数学而且推导的也不是很详细，我也没太看明白就暂且先跳过，这一部分权当是对变分自编码器的简单了解）

变分自编码器 vs 自编码器

传统的自编码器的隐藏层空间是不连续的，其由样本点编码构成，如果输入样本中没有那么在隐藏层中也就没有对应的特征，解码器也就不能给出有意义的输出。而变分自编码器则是要建模样本的分布\(p(x)\)，所以之后解码器可以生成样本。

4.3 word2vec：基于对比损失的方法

Word2vec模型将词嵌入到一个向量空间中，用低维的向量表达每个词，并且语义相关的词距离更近。

Skip-gram词向量模型

Word2vec的核心思想是用一个词的上下文去刻画这个词，对应的有两种模型：给定某个中心词的上下文去预测中心词，CBow模型；给定一个中心词预测其上下文词，Skip-gram模型。

给定一个表示长度为N的语料库的序列\(C=\{w_1,...,w_N\}\)，单词词表为V，有\(w_i\in V\)。Skip-gram模型使用中心词预测上下文，定义上下文词为以中心词为中心的某个窗口内的词，窗口大小为\(2m+1\)。我们希望的事给定某个中心词，输出词为上下文的概率最大。

看下图，对于一个文本，选择中心词“网络”，取\(m=2\)，以中心词及其上下文词构成的单词为正样本\(D\)，否则构成负样本\(\bar D\)。

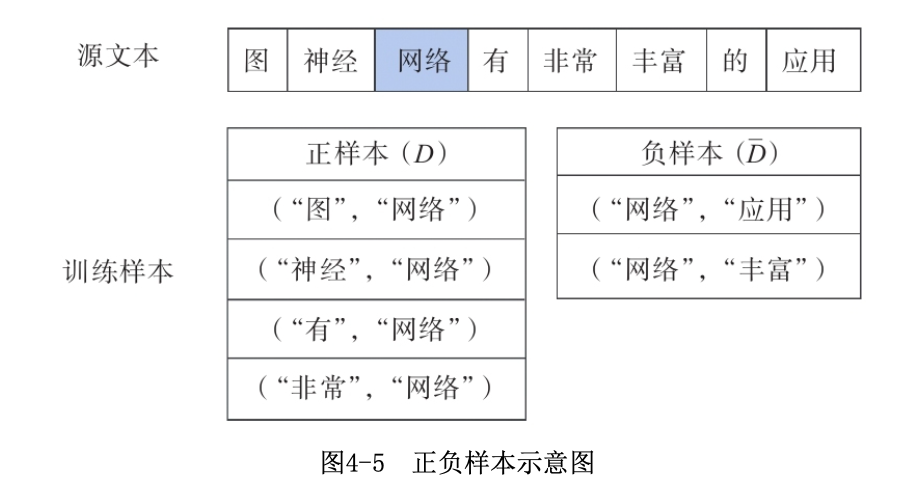
对正负样本定义标签\(\text{label}=\begin{cases}y=1 & \text{if }(w_c,w)\in D\\ y=0 & \text{if }(w_c,w)\in \bar D \end{cases}\)。

我们的目的是找到条件概率\(p(y=1|(w_c,w))\)和\(p(y=0|(w_c,w))\)最大化的参数\(\theta\)：\(\theta'=argmax\prod_{(w_c,w)\in D}p(y=1|(w_c,w);\theta)\prod_{(w_c,w)\in \bar D}p(y=0|(w_c,w);\theta)\)。

这样就得到了一个二分类的问题，任意给定两个词判断是否是上下文词，可以用逻辑回归来建模这个问题。引入矩阵\(U\in R^{|D|\times d},V\in R^{|D|\times d}\)，每一行代表着一个词，前者代表词作为中心词的表达，而后者代表词作为上下文词的表达。那么可以得到\(p(y|(w_c,w))=\begin{cases}\sigma(U_{w_c}·V_w)&\text{if }y=1 \\ 1-\sigma(U_{w_c}·V_w)&\text{if }y=0 \end{cases}\)，其中\(\sigma\)为Sigmoid函数。

联合前面的得到的公式，最后有Skip-gram的目标函数：

\(\begin{aligned}L&=-\Sigma_{(w_c,w)\in D}\text{log}\sigma(U_{w_c}V_w)-\Sigma_{(w_c,w)\in \bar D}\text{log}(1-\sigma(U_{w_c}V_w))\\&=-\Sigma_{(w_c,w)\in D}\text{log}\sigma(U_{w_c}V_w)-\Sigma_{(w_c,w)\in \bar D}\text{log}\sigma(-U_{w_c}V_w)\end{aligned}\)

这个式子一方面在增大正样本的概率，另一方面在减少负样本的概率。实际上增大正样本的概率就是在增大\(U_{w_c}V_w\)，即中心词语上下文词的内积。这种方式作为监督信号指导模型进行学习，模型收敛之后\(U,V\)就是我们需要的词向量，通常我们取\(U\)作为最终的词向量。

构建正样本最大化正样本最小化负样本之间的相似度的方式是表示学习中构建损失函数一种常用的思路，这类损失被称为对比损失，数据及其邻居在输入空间中的关系仍然能够被保留。不同任务中数据的邻居关系可能是不同的，这里邻居关系是上下文词。

负采样

通常情况下负样本的数量远比正样本多，这使得对负样本的计算会成为整体计算的瓶颈。容易想到的解决方案就是在对负样本进行采样来降低计算复杂度。采样时一般不使用均匀采样，而是采用以词频为权重的带权采样。