欧几里德与扩展欧几里德

扩展欧几里德的概念：　　

　　对于不完全为 0 的非负整数 a，b，gcd（a，b）表示 a，b 的最大公约数，必然存在整数对 x，y ，使得 gcd（a，b）=ax+by。

 

x , y 的求解过程如下：

　　　　gcd(a,b) = ax1 + by1

　　　　gcd(b,a%b) = bx2 + (a%b)y2

　　　　由朴素的欧几里德原理得 ， gcd(a,b) = gcd(b,a%b)

　　　　所以 ax1 + by1 = bx2 + (a%b)*y2

　　　　所以 ax1 + by1 = bx2 + (a-(a/b)*b)*y2

　　　　　　　　　　    = ay2 + bx2 - ((a/b)*b)*y2

　　　　　　　　　　　= ay2 + b*(x2-(a/b)*y2)

　　　

　　　　所以  x1 = y2

　　　　　　  y1 = x2 - (a/b)*y2　　

　　　

 

可由递归求得

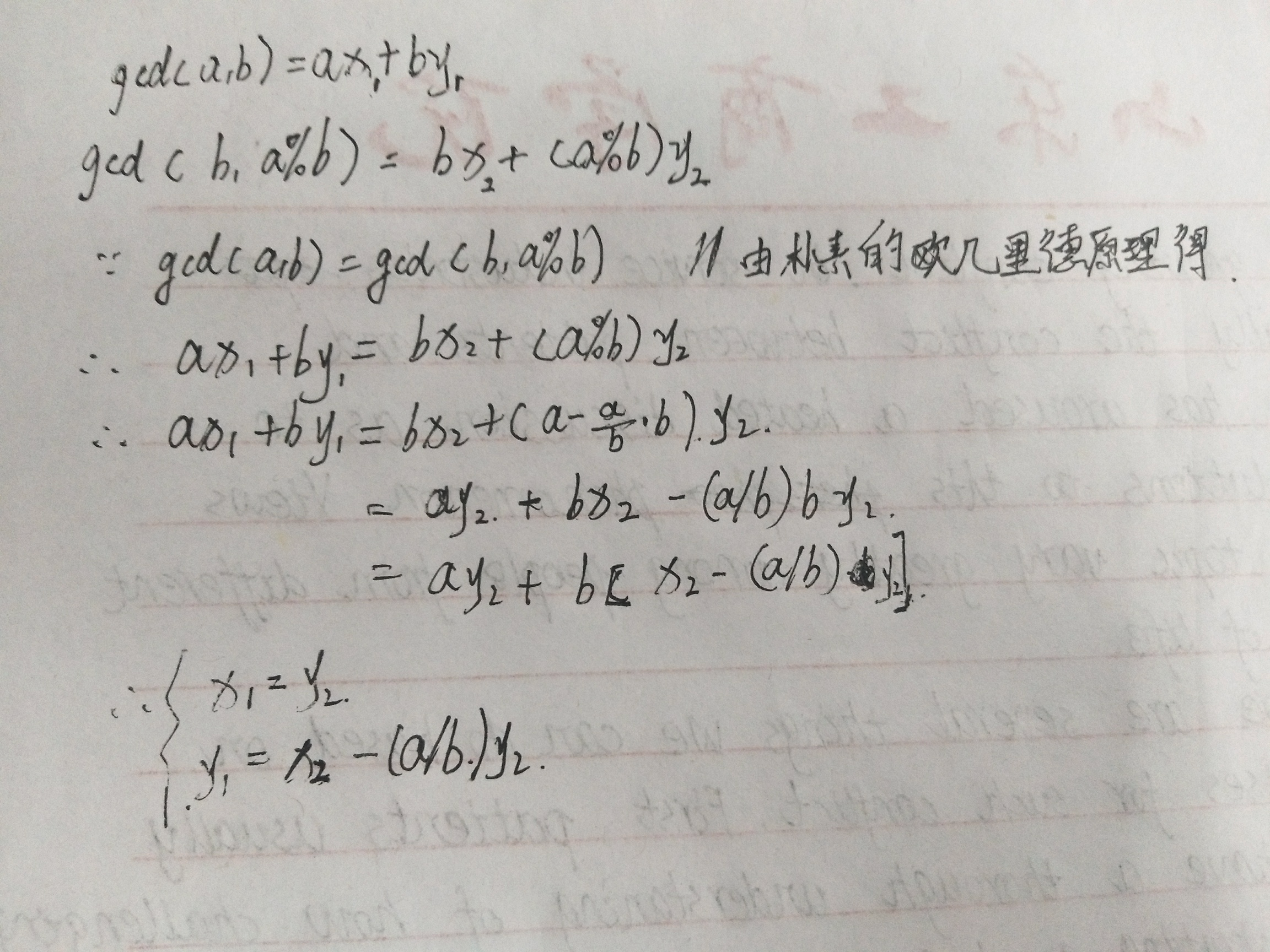
求解 x , y 的代码：

 1 int exgcd(int a,int b,int &x,int &y)
 2 {
 3     if(b==0)
 4     {
 5         x=1;
 6         y=0;
 7         return a;　　　　//a为gcd(a,b)
 8     }
 9     int r=exgcd(b,a%b,x,y);
10     int t=x;
11     x=y;
12     y=t-a/b*y;　　　　　　//返回解得的x和y
13     return r;
14 }

扩展欧几里德的代码得到三个有用的值，分别为a、b的最大公约数，解得的x和y的值。

它的主要应用见大佬的博客：https://www.cnblogs.com/frog112111/archive/2012/08/19/2646012.html