JS 对数据进行 正态分布拟合对比（echarts 做图）

对一组看似正态分布的数据进行标准正态分布的拟合，用来做对比

准备：math.js

给定一组数据

yData = [
53, 53, 58.5, 78, 115, 154.5, 200, 300.5, 383.5, 518, 871.5, 1382.5, 2192.5, 3340.5, 5249, 8979.5, 15448, 26225, 44057.5, 71392, 109113, 159006, 224595.5, 307191.5, 405623, 520332, 646965.5, 785170.5, 930962.5, 1078572.5, 1227179.5, 1373870, 1522723.5, 1671622.5, 1812839.5, 1944963, 2068185, 2180604.5, 2280685.5, 2361196.5, 2417123.5, 2457786, 2483891, 2494890, 2496943.5, 2498862.5, 2500857.5, 2500175, 2501485, 2499141, 2492862, 2478390, 2459869.5, 2443707, 2430140, 2421345.5, 2404805, 2377592.5, 2334130, 2263164, 2163510.5, 2031018.5, 1872739.5, 1698482, 1507286, 1306381.5, 1114865.5, 938499, 771654.5, 619227.5, 488654.5, 379699.5, 289925.5, 218837.5, 165510.5, 126806, 97552, 75560, 59062, 46304.5, 36476, 28583, 22280.5, 16965.5, 12631.5, 9265.5, 6629, 4548.5, 3091, 2102.5, 1396.5, 921, 580, 345, 203.5, 137, 87, 46, 27.5, 12, 6
]

xData=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100]

绘制的图形如下

 

 

 现在要对这个曲线进行正态分布的拟合

　　1.求出均值

　　　　

var yArr = [];var sumFuc = (s, c) => formulaCalcByFunc(s + c, 6);//求和匿名函数，formulaCalc为了减少精度误差，可以自己写var ysum = yData.reduce(sumFuc, 0);
for (var n = 0; n < yData.length; n++) {
var y = yData[n] / ysum;
yArr.push(y);
}
var avg = math.mean(yArr);

 

　　2.编写最小二乘法高斯拟合函数

function gaussFit(xOriginal, yOriginal, average) {
    var x = [];
    var y = [];
    // 过滤平滑部分
    for (var i = 0; i < yOriginal.length; i++)
        if (yOriginal[i] > average) {
            x.push(xOriginal[i]);
            y.push(yOriginal[i]);
        }

    var zMatrix = math.matrix(math.log(y));
    var zMatrixT = math.transpose(zMatrix);
    var xMatrix = math.ones([y.length, 3]);

    for (var j = 0; j < y.length; j++) {
        xMatrix[j][1] = x[j];
        xMatrix[j][2] = x[j] * x[j];
    }
    // 最小二乘法
    var xMatrixT = math.transpose(xMatrix);
    var bMatrix = math.multiply(math.multiply(math.inv(math.multiply(xMatrixT,xMatrix)), xMatrixT), zMatrixT);

    var b2 = math.subset(bMatrix, math.index(2));
    var b1 = math.subset(bMatrix, math.index(1));
    var b0 = math.subset(bMatrix, math.index(0));

    var s = -1 / b2;
    var xMaxi = s * b1 / 2;//均值
    var yMaxi = math.exp(b0 + xMaxi * xMaxi / s);//正态分布归一系数

    var yFit = []
    for (var n = 0; n < yOriginal.length; n++) {
        yFit.push(gaussFunc(xOriginal[n], xMaxi, yMaxi, s));
    }

    return yFit;
}

//正态分布公式
function gaussFunc(x, xMaxi, yMaxi, s) {

return yMaxi * math.exp(-((x - xMaxi) * (x - xMaxi) / s));
}

　　3.求出y轴数据的系数，并还原出原始数据

datas2 = gaussFit(xArr, yArr, avg);
for (var k = 0; k < datas2.length; k++) {
    var l = datas2[k] / yArr[k];
    var y = yData[k] * l;
    yData2.push(y);
}

 

 

最终绘制的图形如下：

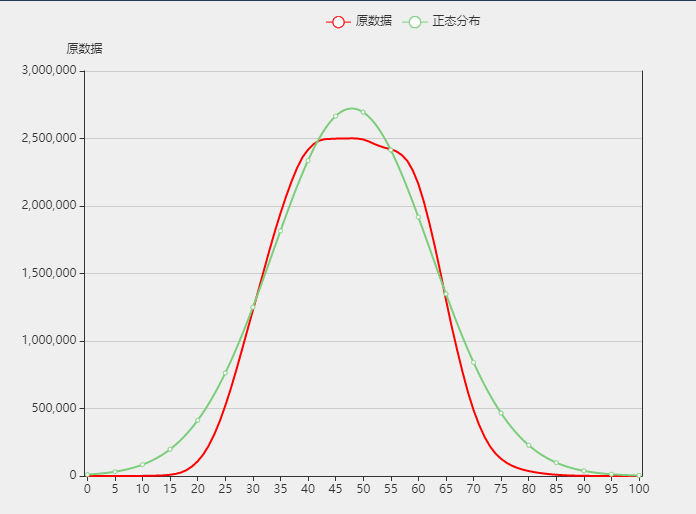
 第二种方法，使用标准正态分布公式实现（结果将会偏向原始数据峰值）：

/**
* 正态分布函数
* @@param x 数据
* @@param mean 平均数
* @@param stdev 标准差
*/
function normalDistributionfun(x, mean, stdev) {
    return (1 / (Math.sqrt(2 * Math.PI) * stdev)) * Math.exp(-1 * ((x - mean) * (x - mean)) / (2 * stdev * stdev));
}


function calcNormallineDta(xData, yData) {
            var result = [];
         
            var totalCount = 0;

            var firstMode = 0;//峰值起始位置
            var modeCount = 0;//找到目前数据的峰值
        
            for (var i = 0; i < yData.length;i++) {
                totalCount += yData[i];
                if (yData[i] > modeCount) {
                    modeCount = yData[i];
                    firstMode = i;
                }
             
            }
            //找出出x轴左右范围内的均值(关键代码)
            var mode = 0;
            var modeDuplicates = 0;
        
            var fellOffTop = true;

            for (var j = firstMode; j < yData.length; j ++) {
                if (yData[j] > yData[firstMode] - (yData[firstMode]/10)) {//10：分布线系数
                    mode += j ;
                    modeDuplicates++;
                }
                else {
                    fellOffTop = false;
                    break;
                }
            }

            var fellOffBottom = true;
        
            for (var k=firstMode-1;k>=0;k--) {
                if (yData[k] > yData[firstMode] - (yData[firstMode] / 10)) {//10：分布线系数
                    mode += k;
                    modeDuplicates++;
                }
                else {
                    fellOffBottom = false;
                    break;
                }
            }
            var mean;
            if (fellOffBottom || fellOffTop) {
               
                mean = firstMode;
            }
            else {
                mean = mode/ modeDuplicates;
            }
            //求出标准差
          
            var stdev = 0;
        
            for (var n = 0; n < yData.length;n++) {
                stdev += Math.pow((n - mean), 2) * yData[n];
            }
        
            stdev /= totalCount-1;
        
            stdev = Math.sqrt(stdev);
            //带入正态分布公式
            for (var m = 0; m < yData.length;m++) {
                var probability =normalDistributionfun(m,mean,stdev);
                result.push(Math.round(probability * totalCount*100)/100);
            }
            return result;
        }
      

 

 

 

 

 完整代码在echart作品上查看

作品地址：https://www.makeapie.com/editor.html?c=xBtzYvoXr2