2023-08-09 00:13阅读: 1413评论: 1推荐: 1

二次规划问题和常见求解框架

二次规划问题

Quadratic Program，QP

二次规划问题是非线性规划（Non-linear program，NLP）问题的特例，即当目标函数 $f$ 为二次型且约束 $h$ ， $g$ 在 $x \in \mathbf{R}^n$ 为线性约束时的 NLP 问题即为 QP 问题，其一般形式如下：

min f (x) = \frac{1}{2} x^{⊺} B x - x^{⊺} b, x \in R^{n} \begin{aligned} s . t . & A_{1} x = c \\ A_{2} x \leq d \end{aligned}

$\min\quad f(x) = \frac{1}{2}\mathbf{x}^\intercal \mathbf{B}\mathbf{x} - \mathbf{x}^\intercal \mathbf{b}, \mathbf{x} \in \mathbb{R}^n\\ \begin{align*} \mathrm{s.t.} & \quad\mathbf{A}_1\mathbf{x} = \mathbf{c} \\ & \quad \mathbf{A}_2\mathbf{x} \le \mathbf{d} \end{align*}$

上式中， $\mathbf{B}\in \mathbb{R}^{n \times n}$ 是对称矩阵, $\mathbf{b}\in \mathbb{R}^n$ , $\mathbf{A}_1\in\mathbb{R}^{m\times n}$ , $c \in \mathbb{R}^n$ $, \mathbf{A}_2\in\mathbb{R}^{p\times n}$ , $\mathbf{d}\in\mathbb{R}^p$

LASSO 问题

LASSO 回归问题是在线性回归问题的基础上，加上 $l_1$ 范数约束，来限制线性拟合的系数，保持一定的稀疏性。相比于岭回归 ( $l_2-norm$ 范数约束)，LASSO 回归对离群极端值具有较好的鲁棒性。LASSO 问题的形式如下：

min_{x} \frac{1}{2} ‖ A x - b ‖_{2}^{2} + γ ‖ x ‖_{1}

$\min _{x} \quad \frac{1}{2}\|\mathbf{A} \mathbf{x}-\mathbf{b}\|_{2}^{2}+\gamma\|\mathbf{x}\|_{1}$

其中为系数向量 , 是数据矩阵， $\lambda>0$ 是惩罚项权重。

LASSO 问题的等价二次规划问题为

\begin{array}{ll} minimize & \frac{1}{2} y^{T} y + γ 1^{T} t \\ subject to & y = A x - b \\ - t \leq x \leq t \end{array}

$\begin{array}{ll} \text { minimize } & \frac{1}{2} \mathbf{y}^{T} \mathbf{y}+\gamma \mathbf{1}^{T} t \\ \text { subject to } & \mathbf{y}=\mathbf{A} \mathbf{x}-\mathbf{b} \\ & -\mathbf{t} \leq \mathbf{x} \leq \mathbf{t} \end{array}$

半二次分裂算法

Half quadratic splitting，HQS

变量分裂法（Variable Spliting）

用于解决目标函数是两个函数之和的优化问题，如假设 g 是 n 维向量到 d 维向量的一个映射，优化目标函数为：

min_{u \in K^{n}} f_{1} (u) + f_{2} (g (u))

$\min_{u\in\mathbb{K}^n}\quad f_1(\mathbf{u})+f_2(g(\mathbf{u}))$

可以通过变量分裂将上式变为：

min_{u \in K^{n}} f_{1} (u) + f_{2} (v) s . t . g (u) = v

$\min_{u\in\mathbb{K}^n}\quad f_1(\mathbf{u})+f_2(\mathbf{v})\\ \mathrm{s.t.} \quad g(\mathbf{u})=\mathbf{v}$

变量分裂之后可能比原问题更好解决。

半二次分裂

通常是将正则项中的原始变量进行变量替换，而后通过增广拉格朗日法（Augmented Lagrange Method，ALM）重写目标函数（包含原数据保真项，拉格朗日乘子项和二次惩罚项，这么做的目的是解耦的同时，简化计算。图像复原中，目标函数为：

\hat{x} = \arg min_{x} \frac{1}{2} ‖ y - H x ‖^{2} + λ Φ (x)

$\hat{\mathbf{x}}=\arg \min _{\mathbf{x}} \frac{1}{2}\|\mathbf{y}-\mathbf{H} \mathbf{x}\|^{2}+\lambda \Phi(\mathbf{x})$

前一项为数据保真项（fidelity），后一项为惩罚项，通常只与去噪有关。通过 HQS 算法，引入辅助变量 z，把惩罚项的 x 替换为 z，并添加相应的等式约束条件：

\hat{x} = \arg min_{x} \frac{1}{2} ‖ y - H x ‖^{2} + λ Φ (z) s.t. z = x

$\hat{\mathbf{x}}=\arg \min _{\mathbf{x}} \frac{1}{2}\|\mathbf{y}-\mathbf{H} \mathbf{x}\|^{2}+\lambda \Phi(\mathbf{z}) \quad \text { s.t. } \quad \mathbf{z}=\mathbf{x}$

由增广拉格朗日法（Augmented Lagrange Method，ALM）得到增广拉格朗日函数：

L_{μ} (x, z) = \frac{1}{2} ‖ y - H x ‖^{2} + λ Φ (z) + \frac{μ}{2} ‖ z - x ‖^{2}

$\mathcal{L}_{\mu}(\mathbf{x}, \mathbf{z})=\frac{1}{2}\|\mathbf{y}-\mathbf{Hx}\|^{2}+\lambda \Phi(\mathbf{z})+\frac{\mu}{2}\|\mathbf{z}-\mathbf{x}\|^{2}$

迭代求解：

\begin{array}{l} x_{k + 1} = \arg min_{x} ‖ y - H x ‖^{2} + μ {‖ x - z_{k} ‖}^{2} \\ z_{k + 1} = \arg min_{z} \frac{μ}{2} {‖ z - x_{k + 1} ‖}^{2} + λ Φ (z) \end{array}

$\begin{array}{l} \mathbf{x}_{k+1}=\arg \min _{\mathrm{x}}\|\mathbf{y}-\mathbf{Hx}\|^{2}+\mu\left\|\mathbf{x}-\mathbf{z}_{k}\right\|^{2} \\ \mathbf{z}_{k+1}=\arg \min _{\mathrm{z}} \frac{\mu}{2}\left\|\mathbf{z}-\mathbf{x}_{k+1}\right\|^{2}+\lambda \Phi(\mathbf{z}) \end{array}$

两个子问题将原问题的保真项和先验项解耦分别求解。

（加速）迭代收缩阈值算法

(Fast) iterative shrinkage-thresholding algorithm, (F)ISTA

近端梯度下降

Proximal Gradient Algorithm, PGD

对于包含不可微部分的优化目标如 lasso 回归的求解，梯度下降等算法已不再适用。近端梯度下降即被用来解决包含不可导项的优化问题。研究如下问题：

min_{x} g (x) + h (x)

$\min_x \quad g(\mathbf{x})+h(\mathbf{x})$

其中， $g(x)$ 是连续可导凸函数； $h(x)$ 是连续的凸函数，可以是不光滑的（不可导，not necessarily differentiable）。对于函数 $f(x)$ ，将其在 $x_0$ 处做二阶泰勒展开，将其用来近似原函数得：

f (x) \approx f (x_{0}) + \nabla f {(x_{0})}^{T} (x - x_{0}) + \frac{1}{2} {(x - x_{0})}^{T} \nabla^{2} f (x) (x - x_{0})

$f(\mathbf{x}) \approx f\left(\mathbf{x}_{0}\right)+\nabla f\left(\mathbf{x}_{0}\right)^{T}\left(\mathbf{x}-\mathbf{x}_{0}\right)+\frac{1}{2}\left(\mathbf{x}-\mathbf{x}_{0}\right)^{T} \nabla^{2} f(\mathbf{x})\left(\mathbf{x}-\mathbf{x}_{0}\right)$

二阶导相对一阶导要难求很多，并且从时间复杂度的角度上来讲，求二阶导信息即 Hessian 矩阵要花去许多时间。根据Lipschitz continuous gradient，我们将二阶导用 $\frac{1}{t}I_n$ 代替，其中 $t\gt 0$ ， $I_n$ 为 n 阶单位矩阵，则

f (x) \approx f (x_{0}) + \nabla f {(x_{0})}^{T} (x - x_{0}) + \frac{1}{2 t} ‖ (x - x_{0} ‖_{2}^{2}

$f(\mathbf{x}) \approx f\left(\mathbf{x}_{0}\right)+\nabla f\left(\mathbf{x}_{0}\right)^{T}\left(\mathbf{x}-\mathbf{x}_{0}\right)+\frac{1}{2t}\|(\mathbf{x}-\mathbf{x}_{0}\|_2^2$

设原问题最优解为 $x^+$ ，则带入上式到原问题，并抛掉常数 $f(x_0)$ ，凑平方得

\begin{aligned} x^{+} & = \underset{x}{\arg min} {f (x_{0}) + \nabla f {(x_{0})}^{T} (x - x_{0}) + \frac{1}{2 t} {‖ x - x_{0} ‖}_{2}^{2} + h (x)} \\ = \underset{x}{\arg min} {\frac{1}{2 t} ‖ x - (x_{0} - t \nabla f (x_{0}) ‖_{2}^{2} + h (x)} \end{aligned}

$\begin{aligned} \mathbf{x}^{+} &=\underset{\mathbf{x}}{\arg \min }\left\{f\left(\mathbf{x}_{0}\right)+\nabla f\left(\mathbf{x}_{0}\right)^{T}\left(\mathbf{x}-\mathbf{x}_{0}\right)+\frac{1}{2 t}\left\|\mathbf{x}-\mathbf{x}_{0}\right\|_{2}^{2}+h(\mathbf{x})\right\} \\ &=\underset{\mathbf{x}}{\arg \min }\left\{\frac{1}{2 t} \| \mathbf{x}-\left(\mathbf{x}_{0}-t \nabla f\left(\mathbf{x}_{0}\right) \|_{2}^{2}+h(\mathbf{x})\right\}\right. \end{aligned}$

定义临近点算子/近端算子 (proximal operator) 如下：

{prox}_{t, h (\cdot)} (z) = \underset{x}{\arg min} {\frac{1}{2 t} ‖ x - z ‖_{2}^{2} + h (x)}

$\operatorname{prox}_{t, h(\cdot)}(\mathbf{z})=\underset{\mathbf{x}}{\arg \min }\left\{\frac{1}{2 t}\|\mathbf{x}-\mathbf{z}\|_{2}^{2}+h(\mathbf{x})\right\}$

等价定义如下：

{prox}_{t, h (\cdot)} (z) = \underset{x}{\arg min} {\frac{1}{2} ‖ x - z ‖_{2}^{2} + t h (x)}

$\operatorname{prox}_{t, h(\cdot)}(\mathbf{z})=\underset{\mathbf{x}}{\arg \min }\left\{\frac{1}{2}\|\mathbf{x}-\mathbf{z}\|_{2}^{2}+th(\mathbf{x})\right\} \\$

利用近端算子可以将原问题的最优解写为:

x^{+} = {prox}_{t, h ((\cdot))} (x_{0} - t \nabla f (x_{0}))

$\mathbf{x}^+ = \operatorname{prox}_{t,h((\cdot))}(\mathbf{x}_0 - t\nabla f(\mathbf{x}_0))$

写为迭代求解形式（近端梯度下降的核心公式）为：

x^{k} = {prox}_{t, h ((\cdot))} (x^{k - 1} - t \nabla f (x^{k - 1}))

$\mathbf{x}^k = \operatorname{prox}_{t,h((\cdot))}(\mathbf{x}^{k-1} - t\nabla f(\mathbf{x}^{k-1}))$

针对不同的 $h(\cdot)$ ，如 $l_0$ 范数、 $l_1$ 范数、 $l_2$ 范数、二次函数等，近端算子都有着对应的闭式解 (closed-form)（或者说显式解），下面列出了几个简单的情况:

$h(\cdot) = 0$ 时， $\operatorname{prox}_{t,h(\cdot)}(\mathbf{z}) = \mathbf{z}$ $h(\cdot) = |\cdot|_0$ 时， $\operatorname{prox}_{t,h(\cdot)}(z_i) =\left\{\begin{array}{ll} z_{i} & \lvert z_{i} \rvert \geq t \\ 0 & \text { otherwise } \end{array}\right.$ ，Elementwise hard-thresholding (硬阈值函数)

$h(\cdot) =|\cdot|_1$ 时， $\operatorname{prox}_{t,h(\cdot)}(z_i) = sign(z_i)\max(|z_i|-t, 0)$ ，Elementwise soft-thresholding (软阈值函数)

$h(\cdot) =|\cdot|_2$ 时， $\operatorname{prox}{t,h(\cdot)}(\mathbf{z}) = \mathbf{z} \odot\left[1-\frac{t}{|\mathbf{z}|_2}\right]_{+}$ ，Elementwise soft-thresholding (软阈值函数)

有时候在不同论文里面会看到 $(a)_+$ 这种数学表达式，它其实就等价于 $max(a,0)$

迭代收缩阈值算法

iterative shrinkage-thresholding algorithm，ISTA

一般的，我们将解决上述含不可导项的优化问题的近端梯度下降算法成为 ISTA 算法。具体应用中，ISTA 算法狭义上一般指不可导项为 $l_1$ 范数的 LASSO 问题。

LASSO 问题中使用了 $l_1$ 范数，故对应 $h(\cdot ) = \lambda |\cdot|_1$ 的情况，此时的近端梯度下降迭代表达式可以写成：

x^{k} = {prox}_{t, λ ‖ \cdot ‖_{1}} (x^{k - 1} - t \nabla f (x^{k - 1})) = S_{λ t} (x^{k - 1} - t \nabla f (x^{k - 1}))

$\mathbf{x}^k = \operatorname{prox}_{t,\lambda \|\cdot\|_1}(\mathbf{x}^{k-1} - t\nabla f(\mathbf{x}^{k-1})) = \operatorname{S}_{\lambda t}(\mathbf{x}^{k-1} - t\nabla f(\mathbf{x}^{k-1}) )$

其中 $\operatorname{S}_{\lambda t}(\cdot)$ 称为软阈值算子（soft-thresholding operator），也常写作 $\operatorname{soft}_{\lambda t}(\cdot)$ ，可以看到该算子即为近端算子中 $h(\cdot) =|\cdot|_1$ 的情况。

若 $z$ 为标量，则有：

{prox}_{t, λ ‖ \cdot ‖_{1}} (z) = S_{λ t} (z) = s i g n (z) max (| z | - λ t, 0) = {\begin{cases} z - λ t & z > λ t \\ 0 & - λ t \leq z \leq λ t \\ z + λ t & z < - λ t \end{cases}

$\operatorname{prox}_{t,\lambda \|\cdot\|_1}(z) = \operatorname{S}_{\lambda t}(z) = sign(z) \max(|z|-\lambda t,0) =\left\{\begin{array}{ll} z-\lambda t & z \gt \lambda t \\ 0 & -\lambda t \le z \le \lambda t \\ z+\lambda t & z \lt - \lambda t \\ \end{array}\right.$

若 $\mathbf{z} = [z_1,\cdots,z_n]^\intercal\in\mathbb{R}^n$ 为向量，则 $\operatorname{S}_{\lambda t}(\mathbf{z}) =[\operatorname{S}_{\lambda t}(z_1),\cdots,\operatorname{S}_{\lambda t}(z_n)]^\intercal$ ，即为每个分量均做软阈值操作。进一步可以推导出如下表达式:

\begin{aligned} S_{λ t} (z_{i}) & = sign (z_{i}) max (| z_{i} | - t, 0) \\ = sign (z_{i}) | z_{i} | max (\frac{| z_{i} | - t}{| z_{i} |}, 0) \\ = z_{i} max (\frac{| z_{i} | - t}{| z_{i} |}, 0) \\ = z_{i} max (1 - \frac{t}{| z_{i} |}, 0) \\ ∴ S_{λ t} (z) = z ⊙ {[1 - \frac{t}{| z |}]}_{+} \end{aligned}

$\begin{aligned} S_{\lambda t}\left(z_{i}\right) &=\operatorname{sign}\left(z_{i}\right) \max \left(\left|z_{i}\right|-t, 0\right) \\ &=\operatorname{sign}\left(z_{i}\right)\left|z_{i}\right| \max \left(\frac{\left|z_{i}\right|-t}{\left|z_{i}\right|}, 0\right) \\ &=z_{i} \max \left(\frac{\left|z_{i}\right|-t}{\left|z_{i}\right|}, 0\right) \\ &=z_{i} \max \left(1-\frac{t}{\left|z_{i}\right|}, 0\right) \\ & \therefore S_{\lambda t}(\mathbf{z})=\mathbf{z} \odot\left[1-\frac{t}{|\mathbf{z}|}\right]_{+} \end{aligned}$

其中， $|z|$ 为对向量 $\mathbf{z}$ 的每个分量取绝对值后组成的向量； $[\cdot]_+$ 表示取正，即 $\max (\cdot,0)$ ; $\mathbf{A} \odot\mathbf{B}$ 表示两个矩阵的 Hadamard 乘积（element-wise product）。

软阈值迭代算法 (ISTA, iterative soft-thresholding algorithm)，即为用软阈值作为包含 $l_1$ 范数的目标函数的“梯度”，使用”梯度下降“来得到最优值的算法。回顾 LASSO 优化问题，可以得到:

\nabla f (x) = \nabla \frac{1}{2} ‖ A x - b ‖_{2} = A^{⊺} (A x - b) h (x) = γ ‖ x ‖_{1}

$\nabla f(x) = \nabla \frac{1}{2}\|\mathbf{A}\mathbf{x}-\mathbf{b}\|_2 = \mathbf{A}^\intercal(\mathbf{A}\mathbf{x}-\mathbf{b})\\ h(x) = \gamma \|x\|_1$

所以 ISTA 算法的迭代公式为：

x^{k} = S_{γ t} (x^{k - 1} - t \nabla f (x^{k - 1})) = S_{γ t} (x^{k - 1} - t A^{⊺} (A x^{k - 1} - b))

$\mathbf{x}^k = \operatorname{S}_{\gamma t}(\mathbf{x}^{k-1} - t\nabla f(\mathbf{x}^{k-1}) ) = \operatorname{S}_{\gamma t}(\mathbf{x}^{k-1} - t\mathbf{A}^\intercal(\mathbf{A}\mathbf{x}^{k-1}-\mathbf{b}))$

算法流程如下（该算法流程为一般形式的 ISTA 算法流程，即近端算子 $p_L(\cdot)$ 为不可导项 $h(\cdot)$ 对应的近端算子，特殊的，当不可导项 $h(\cdot)$ 为 $l_1$ 范数时， $p_L(\cdot) = S_{rt}(\cdot)$ ，下同）：

ISTA 算法还有一种推广形式的迭代公式：

x^{k} = (1 - β) x^{k - 1} + β S_{γ t} (x^{k - 1} - A^{⊺} (A x^{k - 1} - b))

$\mathbf{x}^k = (1-\beta)\mathbf{x}^{k-1} + \beta \operatorname{S}_{\gamma t}(\mathbf{x}^{k-1} - \mathbf{A}^\intercal(\mathbf{A}\mathbf{x}^{k-1}-\mathbf{b}))$

其中 $\beta \gt 0$ 。原始 ISTA 算法的迭代形式可以看做 $\beta =1$ 的特例。当 $\beta \gt 1$ 或者 $\beta \lt 1$ 时可以将推广形式看做原始形式的 over/under related 版本。

文献中已经证明，当迭代步长取 $f$ 的 Lipschitz 常数的倒数（即 $\frac{1}{L(f)}$ ）时，由 ISTA 算法生成的序列 $\mathbf{x_k}$ 的收敛速度为 $\mathcal{O}(\frac{1}{k})$ 显然为次线性收敛速度。然而固定步长的 ISTA 的缺点是：Lipschitz 常数 $L(f)$ 不一定可知或者可计算。例如，L1 范数约束的优化问题，其 Lipschitz 常数依赖于 $\mathbf{A}^\intercal \mathbf{A}$ 的最大特征值。而对于大规模的问题，非常难计算。因此出现了 ISTA 算法的 Backtracking 版本，通过不断收缩迭代步长的策略使其收敛，算法流程如下：

加速迭代收缩阈值算法

fast iterative shrinkage-thresholding algorithm， FISTA

为了加速 ISTA 算法的收敛，文献中作者采用了著名的梯度加速策略Nesterov加速技术，使得 ISTA 算法的收敛速度从 $\mathcal{O}(\frac{1}{k})$ 变成 $\mathcal{O}(\frac{1}{k^2})$ ，加速的 ISTA 算法称为 FISTA。FISTA 与 ISTA 算法相比，仅仅多了个 Nesterov 加速步骤，以极少的额外计算量大幅提高了算法的收敛速度。而且不仅在 FISTA 算法中，在几乎所有与梯度有关的算法中，Nesterov 加速技术都可以使用。FISTA 的算法流程如下：

当然，考虑到与 ISTA 同样的问题：问题规模大的时候，决定步长的 Lipschitz 常数计算复杂。FISTA 与 ISTA 一样，亦有其回溯算法。在这个问题上，FISTA 与 ISTA 并没有区别，上面也说了，FISTA 与 ISTA 的区别仅仅在于每一步迭代时近似函数起始点的选择。更加简明的说：FISTA 用一种更为聪明的办法选择序列 ${\mathbf{x}_k}$ ，使得其基于梯度下降思想的迭代过程更加快速地趋近问题函数 $f(x)$ 的最小值。

带回溯的 FISTA 算法基本迭代步骤如下：

值得注意的是，在每一步迭代中，计算近似函数的起止点时，FISTA 使用前两次迭代过程的结果 $\mathbf{x}_k,\mathbf{x}_{k-1}$ ，对其进行简单的线性组合生成下一次迭代的近似函数起始点 yk。方法很简单，但效果却非常好。当然，这也是有理论支持的。关于 ISTA 和 FISTA 的具体理论推导可以看原论文。

两步迭代收缩阈值算法

Two-step iterative shrinkage/thresholding, TwIST

TwIST 算法是 ISTA 算法的改进算法，其 two-step 是指该算法的每次迭代都依赖于前两次迭代的结果，而不仅是前一次迭代的结果。(F)ISTA 算法的收敛速度对线性观测矩阵具有很强的依赖性，当观测矩阵十分病态（ill-posed）时，该算法的收敛速度会很慢。TwIST 通过引入两步（或者说二阶， second order）非线性迭代策略克服了 ISTA 收敛速度的问题，在病态问题的求解中具有更快的收敛速度。定义优化目标函数：

min_{x} \frac{1}{2} ‖ y - K x ‖^{2} + λ Φ (x)

$\min_x \quad \frac{1}{2}\|\mathbf{y}-\mathbf{K}\mathbf{x}\|^2+\lambda\Phi(\mathbf{x})$

该目标函数是线性逆问题求解中的常规形式。其中， $y$ 是观察数据， $K$ 是一个线性操作符， $\Phi(\mathbf{x})$ 是一个正则项。该目标函数的第一项为数据保真项，第二项为先验项，二者通过正则化参数 $\lambda$ 控制权重。

TwIST 算法的迭代公式为：

x_{1} = Γ_{λ} (x_{0}) x_{t + 1} = (1 - α) x_{t - 1} + (α - β) x_{t} + β Γ_{λ} (x_{t})

$\mathbf{x}_1 = \Gamma_\lambda(\mathbf{x}_0)\\ \mathbf{x}_{t+1} = (1-\alpha) \mathbf{x}_{t-1} + (\alpha-\beta)\mathbf{x}_t+\beta\Gamma_\lambda(\mathbf{x}_t)$

对于 $t\ge1$ ， $\Gamma_\lambda:\mathbb{R}^m\rightarrow\mathbb{R}^m$ 定义为

Γ_{λ} (x) = Ψ_{λ} (x + K^{⊺} (y - K x))

$\Gamma_\lambda(\mathbf{x}) = \Psi_\lambda(\mathbf{x}+\mathbf{K}^\intercal(\mathbf{y}-\mathbf{K}\mathbf{x}))$

其中 $\Psi_\lambda$ （去噪函数，Moreau proximal mapping）定义为

Ψ_{λ} (y) = \arg min_{x} {\frac{1}{2} ‖ x - y ‖^{2} + λ Φ (x)}

$\Psi_\lambda(y) = \arg \min_x \left\{ \frac{1}{2} \|\mathbf{x} -\mathbf{y}\|^2+\lambda\Phi(\mathbf{x}) \right\}$

当 $\Phi(\mathbf{x}) = |\mathbf{x}|_1$ 时， $\Psi_\lambda(y) = \operatorname{S}_{\lambda}(y) = sign(z) \max(|z|-\lambda ,0)$ 即为软阈值函数。更一般的，当 $\Phi(\mathbf{x})$ 时为全变分（total variation, TV）、加权 $l_p$ 范数以及加权 $l_p$ 范数的 $p\mathrm{th}$ 次方时对应的 $\Psi_\lambda$ 的推导见原论文。

广义交替投影算法

Generalized alternating projection, GAP

考虑优化问题：

min_{w, C} C s . t . ‖ w ‖_{ℓ_{2, 1}^{G β}} \leq C a n d Φ w = y

$\min_{\mathbf{w},C}\quad C \quad \mathrm{s.t.} \quad \|\mathbf{w}\|_{\ell_{2,1}^{\mathcal{G}\beta}} \le C \quad \mathrm{and} \quad \mathbf{\Phi}\mathbf{w}=\mathbf{y}$

该优化问题的本质为寻找一个和给定的线性流形（优化函数第二项）有非空交集的最小加权 $\ell_{2,1}$ 范数球（优化函数第一项）。可以通过一系列交替投影求解该问题，引入辅助变量 $\theta$ 将该问题先进行转化：

(w^{(t)}, θ^{(t)}) = \arg min_{w, θ} \frac{1}{2} ‖ w - θ ‖_{2}^{2} + λ^{(t)} ‖ {θ ‖}_{ℓ_{2, 1}^{G β}} subject to Φ w = y

$\left(\mathbf{w}^{(t)}, \boldsymbol{\theta}^{(t)}\right)=\arg \min _{\mathbf{w} , \boldsymbol{\theta}} \frac{1}{2}\|\mathbf{w}-\boldsymbol{\theta}\|_{2}^{2}+\lambda^{(t)}\|\mathbf{\theta\|}_{\ell_{2,1}^{\mathcal{G}\beta}} \quad \text { subject to } \quad \mathbf{\Phi} \mathbf{w}=\mathbf{y} \\$

其中， $\lambda^{(t)}\ge0$ 是与 $C^{(t)}$ 有关的 Lagrangian 乘子。通过对 $\mathbf{w},\mathbf{\theta}$ 进行交替更新可以求解上述优化问题。具体来说，给定 $\mathbf{\theta}$ 时， $\mathbf{w}$ 的更新是 $\mathbf{\theta}$ 在线性流形上的一个 Euclidean projection；给定 $\mathbf{w}$ ， $\mathbf{\theta}$ 的更新可以通过对 $\mathbf{w}$ 进行 groupwise 的 shrinkage（软阈值操作）来获得，两种情况下的更新都有解析（closed-form）解。具体迭代公式如下（假设 $\mathbf{\Phi}\mathbf{\Phi}^\intercal$ 可逆)：

\begin{array}{ll} (update of λ) & λ^{(t)} = {‖ w_{G_{j_{m}^{⋆} + 1}^{(t)}} ‖}_{2} β_{j_{m^{⋆} + 1}^{- 1} (t)}^{D e f} λ (w^{(t)}, m^{⋆}), m^{⋆} < m \\ (Euclidean projection) & w^{(t)} = θ^{(t - 1)} + Φ^{T} {(Φ Φ^{T})}^{- 1} (y - Φ θ^{(t - 1)}) \\ (groupwise shrinkage) & θ_{G_{k}}^{(t)} = w_{G_{k}}^{(t)} max {1 - λ (w^{(t)}, m^{⋆}) {‖ w_{G_{k}}^{(t)} ‖}_{2}^{- 1} β_{k}, 0} \forall k \in N_{m} \end{array}

$\begin{array}{ll} (\text{update of } \; \lambda) & \lambda^{(t)}=\left\|\mathbf{w}_{\mathcal{G}_{j_{m}^{\star}+1}^{(t)}}\right\|_{2} \beta_{j_{m^{\star}+1}^{-1}(t)}^{D e f} \lambda\left(\mathbf{w}^{(t)}, m^{\star}\right), \quad m^{\star}<m\\ \text{(Euclidean projection)} & \mathbf{w}^{(t)}=\boldsymbol{\theta}^{(t-1)}+\boldsymbol{\Phi}^{T}\left(\boldsymbol{\Phi} \boldsymbol{\Phi}^{T}\right)^{-1}\left(\mathbf{y}-\mathbf{\Phi} \boldsymbol{\theta}^{(t-1)}\right) \\ \text{(groupwise shrinkage)} & \boldsymbol{\theta}_{\mathcal{G}_{k}}^{(t)}=\mathbf{w}_{\mathcal{G}_{k}}^{(t)} \max \left\{1-\lambda(\mathbf{w}^{(t)},m^\star)\left\|\mathbf{w}_{\mathcal{G}_{k}}^{(t)}\right\|_{2}^{-1}\beta_k, 0\right\} \quad \forall k \in \mathbb{N}_{m} \end{array}$

其中关于 $\lambda$ 的更新较为复杂，详细推导见原论文。（关于第二步中 Euclidean projection 解析解的推导：当给定 $\mathbf{\theta}$ 时，更新 $\mathbf{w}$ 的时候，求解的问题变为 $\arg \min_{\mathbf{\mathbf{w}}} \quad \frac{1}{2}|\mathbf{w}-\mathbf{\theta|_2^2}, \quad \mathrm{s.t.} \quad \mathbf{\Phi w}=\mathbf{y}$ ，通过变量替换 $\mathbf{w}^{'} = \mathbf{w}-\mathbf{\theta}$ ，该问题变为矩阵分析中典型的最小范数解的问题，有相应的解析解，带入并反求 $\mathbf{w}$ 即得）

交替方向乘子法

Alternating direction method of multipilers, ADMM

考虑优化问题：

min_{x, z} f (x) + g (z) s . t . A x + B z - c = 0

$\min_{x,z} \quad f(\mathbf{x})+ g(\mathbf{z})\\ \mathrm{s.t.} \quad \mathbf{Ax}+\mathbf{Bz}-\mathbf{c}=0$

ADMM 的算法流程为：

\begin{aligned} x^{k + 1} & = \arg min_{x} f (x) + \frac{ρ}{2} {‖ A x + B z^{k} - c + μ^{k} ‖}_{2}^{2} \\ z^{k + 1} & = \arg min_{z} g (z) + \frac{ρ}{2} {‖ A x^{k + 1} + B z - c + μ^{k} ‖}_{2}^{2}, (μ^{k} := \frac{λ^{k}}{ρ}) \\ μ^{k + 1} & = μ^{k} + (A x^{k + 1} + B z^{k + 1} - c) \end{aligned}

$\begin{aligned} \mathbf{x}^{k+1} &=\arg \min _{\mathbf{x}} f(\mathbf{x})+\frac{\rho}{2}\left\|A \mathbf{x}+B \mathbf{z}^{k}-\mathbf{c}+\boldsymbol{\mu}^{k}\right\|_{2}^{2} \\ \mathbf{z}^{k+1} &=\arg \min _{\mathbf{z}} g(\mathbf{z})+\frac{\rho}{2}\left\|A \mathbf{x}^{k+1}+B \mathbf{z}-\mathbf{c}+\boldsymbol{\mu}^{k}\right\|_{2}^{2}, \quad\left(\boldsymbol{\mu}^{k}:=\frac{\boldsymbol{\lambda}^{k}}{\rho}\right) \\ \boldsymbol{\mu}^{k+1} &=\boldsymbol{\mu}^{k}+\left(A \mathbf{x}^{k+1}+B \mathbf{z}^{k+1}-\mathbf{c}\right) \end{aligned}$

关于 ADMM 的推导过程建议参考 ADMM算法的详细推导过程是什么？ - 覃含章的回答

关于在实际场景中如果将问题转换为 ADMM 形式来求解，推荐参考交替方向乘子法（ADMM）算法的流程和原理是怎样的？ - 门泊东吴的回答，下面摘录其中一例，求解含有 $l_1$ 范数的优化问题：

min_{x, z} l (x) + λ ‖ x ‖_{1}

$\min_{x,z} \quad l(\mathbf{x})+\lambda\|\mathbf{x}\|_1 \\$

s 首先引入辅助变量 $\mathbf{z}$ 将上述问题转换为 ADMM 可以求解的形式：

min_{x, z} l (x) + λ ‖ z ‖_{1} s . t . x - z = 0

$\min_{x,z} \quad l(\mathbf{x})+\lambda\|\mathbf{z}\|_1 \\ \mathrm{s.t.} \quad \mathbf{x}-\mathbf{z}=\mathbf{0}$

使用 ADMM 的求解流程为：

\begin{array}{l} x^{k + 1} = \arg min_{x} l (x) + \frac{ρ}{2} {‖ x - z^{k} + μ^{k} ‖}_{2}^{2} \\ z^{k + 1} = S_{λ / ρ} (x^{k + 1} + μ^{k}) \\ μ^{k + 1} = μ^{k} + (x^{k + 1} - z^{k ⊥ 1}) \\ S_{κ} (a) := {\begin{cases} a - κ, & a > κ \\ 0, & | a | \leq κ \\ a + κ, & a < - κ \end{cases} \end{array}

$\begin{array}{l} \mathbf{x}^{k+1}=\arg \min _{\mathbf{x}} l(\mathbf{x})+\frac{\rho}{2}\left\|\mathbf{x}-\mathbf{z}^{k}+\boldsymbol{\mu}^{k}\right\|_{2}^{2} \\ \mathbf{z}^{k+1}=S_{\lambda / \rho}\left(\mathbf{x}^{k+1}+\boldsymbol{\mu}^{k}\right) \\ \boldsymbol{\mu}^{k+1}=\boldsymbol{\mu}^{k}+\left(\mathbf{x}^{k+1}-\mathbf{z}^{k \perp 1}\right) \\ \operatorname{S}_{\kappa}(a):=\left\{\begin{array}{ll} a-\kappa, & a>\kappa \\ 0, & |a| \leq \kappa \\ a+\kappa, & a<-\kappa \end{array}\right. \end{array}$

其中 $\operatorname{S}_\kappa(a)$ 是软阈值函数。对于 LASSO 问题，上述 $l(x) = \frac{1}{2}|\mathbf{A}\mathbf{x}-\mathbf{b}||^2_2$ ，则 $\mathbf{x}^{k+1}$ 的解析解可以写成： $\mathbf{x}^{k+1} = (\mathbf{A}^\intercal\mathbf{A}+\rho I)^{-1}(\mathbf{A}^\intercal\mathbf{b}+\rho (\mathbf{z}^k-\mathbf{\mu} ^k))$

算子分裂二次规划求解算法

Operator splitting solver for quadratic programs, OSQP

考虑一般的（凸）二次规划（quadratic program，QP）问题：

min_{x} \frac{1}{2} x^{⊺} P x + q^{⊺} x s . t . A x \in C

$\min_x \quad \frac{1}{2}\mathbf{x}^\intercal\mathbf{P}\mathbf{x}+\mathbf{q}^\intercal\mathbf{x}\\ \mathrm{s.t.} \quad \mathbf{Ax}\in\mathcal{C}$

其中 $\mathbf{x} \in \mathbf{R}^n, \mathbf{P}\in\mathbf{S}^n_+,\mathbf{q}\in\mathbf{R}^n;\mathbf{A}\in\mathbf{R}^{m\times n}, \mathcal{C}\subseteq\mathbf{R}^m$

如果集合 $\mathcal{C} =[l,u] = {z\in \mathbf{R}^m | l_i \le z_i \le u_i,i=1,\cdots ,m }$ ，其中 $l_i\in {-\infty }\cup\mathbf{R}, u_i\in \mathbf{R}\cup {+\infty }$ ，则上述问题转化为：

min_{x} \frac{1}{2} x^{⊺} P x + q^{⊺} x s . t . l \leq A x \leq u

$\min_x \quad \frac{1}{2}\mathbf{x}^\intercal\mathbf{P}\mathbf{x}+\mathbf{q}^\intercal\mathbf{x}\\ \mathrm{s.t.} \quad l\le\mathbf{Ax}\le u$

当 $l_i = u_i$ 对所有元素均成立，或者对部分元素成立时，相应约束即变为等式约束。

将上述问题转换为可以利用 ADMM 算法求解的形式：

\begin{array}{ll} minimize & (1 / 2) {\tilde{x}}^{T} P \tilde{x} + q^{T} \tilde{x} + I_{A x = z} (\tilde{x}, \tilde{z}) + I_{C} (z) \\ subject to & (\tilde{x}, \tilde{z}) = (x, z) \end{array}

$\begin{array}{ll} \operatorname{minimize} & (1 / 2) \tilde{x}^{T} P \tilde{x}+q^{T} \tilde{x}+\mathcal{I}_{A x=z}(\tilde{x}, \tilde{z})+\mathcal{I}_{\mathcal{C}}(z) \\ \text { subject to } & (\tilde{x}, \tilde{z})=(x, z) \end{array}$

其中：

I_{A x = z} (x, z) = {\begin{cases} 0 & A x = z \\ + \infty & otherwise \end{cases}, I_{C} (z) = {\begin{cases} 0 & z \in C \\ + \infty & otherwise \end{cases}

$\mathcal{I}_{A x=z}(x, z)=\left\{\begin{array}{ll} 0 & A x=z \\ +\infty & \text { otherwise } \end{array}, \quad \mathcal{I}_{\mathcal{C}}(z)=\left\{\begin{array}{ll} 0 & z \in \mathcal{C} \\ +\infty & \text { otherwise } \end{array}\right.\right.$

利用 ADMM 算法可以将上述优化问题分为三步迭代求解：

其中 $\sigma\gt 0, \rho \gt 0$ 为步长参数， $\alpha\in(0,2)$ 是松弛参数， $\Pi$ 表示向 $\mathcal{C}$ 集合上的欧几里得投影（Euclidean projection）。根据 (16) 和 (18) 可以推出来 $w^{k+1}=0, \forall k \gt 0$ ，所以表示 $w$ 的迭代更新的 (18) 式可以去掉。上述迭代的关键步骤在于 (15) 式，通过 KKT 条件可以推出其解析解为：

[\begin{array}{cc} P + σ I & A^{T} \\ A & - ρ^{- 1} I \end{array}] [\begin{matrix} {\tilde{x}}^{k + 1} \\ ν^{k + 1} \end{matrix}] = [\begin{matrix} σ x^{k} - q \\ z^{k} - ρ^{- 1} y^{k} \end{matrix}]

$\left[\begin{array}{cc} P+\sigma I & A^{T} \\ A & -\rho^{-1} I \end{array}\right]\left[\begin{array}{c} \tilde{x}^{k+1} \\ \nu^{k+1} \end{array}\right]=\left[\begin{array}{c} \sigma x^{k}-q \\ z^{k}-\rho^{-1} y^{k} \end{array}\right]$

{\tilde{z}}^{k + 1} = z^{k} + ρ^{- 1} (v^{k + 1} - y^{k})

$\widetilde{z}^{k+1} = z^k+\rho^{-1}(v^{k+1}-y^k)$

具体推导见原论文。OSQP 算法的迭代步骤具体如下：

上述迭代步骤中，除了步骤 3 之外都很简单，因为它们仅包含向量加减，数乘以及投影操作，而且都是 component-wise separable 的操作，能够很容易的进行并行。下面以 LASSO 问题为例，将其转换为可以用 OSQP 求解的二次规划问题形式：

LASSO 问题的一般形式为：

min_{x} ‖ A x - b ‖^{2} + λ ‖ x ‖_{1}

$\min_x \quad \|\mathbf{Ax}-\mathbf{b}\|^2 + \lambda\|\mathbf{x\|_1}$

其中, $\mathbf{x}\in\mathbf{R}^n$ 是参数向量， $\mathbf{A}\in\mathbf{R}^{m\times n}$ 是数据矩阵， $\lambda$ 是权重参数。将该问题转换为二次规划问题：

\begin{array}{lll} min & y^{⊺} y + λ 1^{⊺} t \\ s . t . & y = A x - b \\ - t \leq x \leq t \end{array}

$\begin{array}{lll} \min \quad & \mathbf{y}^\intercal\mathbf{y}+\lambda \mathbf{1}^\intercal t\\ \mathrm{s.t.} & \mathbf{y} = \mathbf{Ax}-\mathbf{b}\\ &-\mathbf{t} \le \mathbf{x} \le \mathbf{t} \end{array}$

其中 $\mathbf{y}\in\mathbf{R}^m, \mathbf{t}\in\mathbf{R}^n$ 是两个新引入的变量。转化为二次规划形式后的 LASSO 问题即可以用上述 OSQP 算法求解。

附录 Appendix

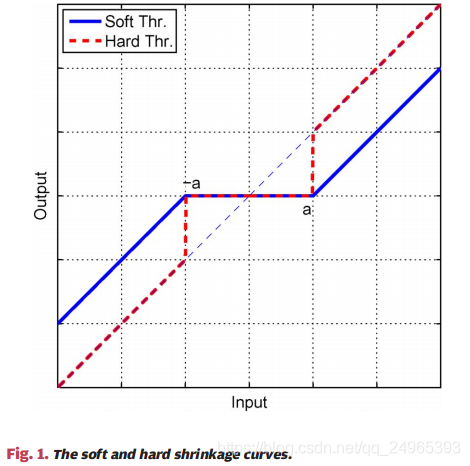
软阈值算子和硬阈值算子

soft-thresholding operator， hard-thresholding operator

软阈值算子的表达式 $\operatorname{soft}_{T}(x) = sign(x)\max(|x|-T,0) =\left\{\begin{array}{ll} x+T & x < -T \\ 0 & \lvert x \rvert \le T \\ x-T & x > T \end{array}\right.$
硬阈值算子的表达式 $\operatorname{hard}_{T}(x) = sign(x)\max(|x|-T,0) =\left\{\begin{array}{ll} x & \lvert x \rvert > T \\ 0 & \lvert x \rvert \le T \end{array}\right.$
二者的图像如下：

Lipschitz 常数和 Lipschitz 连续

利普希茨连续的定义是：如果函数 $f$ 在区间 $\mathcal{Q}$ 上以常数 $L$ 利普希茨连续，那么对于 $x,y\in\mathcal{Q}$ ，有：

‖ f (x) - f (y) ‖ \leq L ‖ x - y ‖

$\|f(x)-f(y)\|\le L\|x-y\|$

其中常数 $L$ 称为 $f$ 在区间 $\mathcal{Q}$ 上的 Lipschitz 常数。除了 Lipschitz continuous 之外，Lipschitz continuous gradient 和 Lipschitz continuous Hessian 也是常用到的概念，它们都是由 Lipschitz continuous 概念延伸出来的。值得一提的是，很多论文中，尤其是关于凸优化的问题，Lipschitz continuous gradient的应用更为常见。

其中，如果函数 $f$ 满足 Lipschitz continuous gradient，就意味着它的导数 $f'$ 满足 Lipschitz continuous，即如果函数 $f$ 满足 Lipschitz continuous gradient，则：

‖ f^{'} (x) - f^{'} (y) ‖ \leq L ‖ x - y ‖

$\|f'(x)-f'(y)\|\le L\|x-y\|$

其中，如果函数 $f$ 满足 Lipschitz continuous Hessian，就意味着它的二阶导数 $f''$ 满足 Lipschitz continuous，即如果函数 $f$ 满足 Lipschitz continuous Hessian，则：

‖ f^{″} (x) - f^{'} (y) ‖ \leq L ‖ x - y ‖

$\|f''(x)-f'(y)\|\le L\|x-y\|$

从上面的定义中可以看出，利普希茨连续限制了函数 $f$ 的局部变动幅度不能超过某常量。同样的道理，Lipschitz continuous gradient 和 Lipschitz continuous Hessian 则限制了函数的导函数和二阶导函数的局部变化幅度。

根据上述第二种 Lipschitz continuous gradient 条件可以有以下定理：

如果函数 $f$ 在 $\mathbb{R}^n$ 上满足 Lipschitz continuous gradient，则对于任意 $x,y\in\mathbb{R}^n$ 有：

| f (y) - f (x) - < f^{'} (x), y - x > | \leq \frac{L}{2} ‖ y - x ‖^{2}

$|f(y)-f(x)-<f'(x),y-x>|\le \frac{L}{2}\|y-x\|^2$

根据上面的公式，去掉绝对值可以得到等价表达：

{\begin{cases} f (y) \leq f (x) + < f^{'} (x), y - x > + \frac{L}{2} ‖ y - x ‖^{2} \\ f (y) \geq f (x) + < f^{'} (x), y - x > - \frac{L}{2} ‖ y - x ‖^{2} \end{cases}

$\left\{ \begin{array} {l} f(y) \le f(x)+<f'(x),y-x>+\frac{L}{2}\|y-x\|^2\\ f(y) \ge f(x)+<f'(x),y-x>-\frac{L}{2}\|y-x\|^2 \end{array} \right .$

其余两种 Lipschitz continuous 条件也有相应的定理，具体定理与证明见论文。

Nesterov 加速技术

Nesterov 加速技术由大神 Yurii Nesterov (内斯特罗夫) 于 1983 年提出来的，它与目前深度学习中用到的经典的动量方法（Momentum method）很相似，和动量方法的区别在于二者用到了不同点的梯度，动量方法采用的是上一步迭代点的梯度，而 Nesterov 方法则采用从上一步迭代点处朝前走一步处的梯度。在几乎所有与梯度有关的算法中，Nesterov 加速技术都可以使用。具体对比如下。

动量方法：

v_{t + 1} = u_{t} v_{t} - α_{t} \nabla g (θ_{t}) θ_{t + 1} = θ_{t} + v_{t + 1}

$v_{t+1} = u_tv_t - \alpha _t \nabla g(\theta _ t)\\ \theta_{t+1} = \theta_t+v_{t+1}$

Nesterov 方法：

v_{t + 1} = u_{t + 1} v_{t} - α_{t} \nabla g (θ_{t} + u_{t} v_{t}) θ_{t + 1} = θ_{t} + v_{t + 1}

$v_{t+1} = u_{t+1}v_t - \alpha_t\nabla g(\theta_t+u_tv_t)\\ \theta_{t+1} = \theta_t+v_{t+1}$

详见 Nesterov加速和Momentum动量方法

Reference

HQS——Half Quadratic Splitting半二次方分裂
近端梯度下降与软阈值迭代：PGD and ISTA
软阈值迭代算法（ISTA）和快速软阈值迭代算法（FISTA）
LASSO回归与L1正则化西瓜书
【优化】利普希茨连续（Lipschitz continuous）及其应用
FISTA的由来：从梯度下降法到ISTA & FISTA
Nesterov加速和Momentum动量方法
IST改进算法之Two-Step Iterative Shrinkage/Thresholding(TwIST)
交替方向乘子法（ADMM）算法的流程和原理是怎样的？
ADMM算法的详细推导过程是什么？ - 覃含章的回答
交替方向乘子法（ADMM）算法的流程和原理是怎样的？ - 门泊东吴的回答
Xiaotian13的博客 -凸优化
Beck, Amir, and Marc Teboulle. “A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems.” SIAM Journal on Imaging Sciences 2, no. 1 (January 2009): 183–202. https://doi.org/10.1137/080716542.
Bioucas-Dias, J.M., and M.A.T. Figueiredo. “A New TwIST: Two-Step Iterative Shrinkage/Thresholding Algorithms for Image Restoration.” IEEE Transactions on Image Processing 16, no. 12 (December 2007): 2992–3004. https://doi.org/10.1109/TIP.2007.909319.
Zhou, Xingyu. “On the Fenchel Duality between Strong Convexity and Lipschitz Continuous Gradient.” ArXiv:1803.06573 [Math], March 17, 2018. http://arxiv.org/abs/1803.06573.
Liao, Xuejun, Hui Li, and Lawrence Carin. “Generalized Alternating Projection for Weighted- $\ell_{2,1}$ Minimization with Applications to Model-Based Compressive Sensing.” SIAM Journal on Imaging Sciences 7, no. 2 (January 2014): 797–823. https://doi.org/10.1137/130936658.
Stellato, Bartolomeo, Goran Banjac, Paul Goulart, Alberto Bemporad, and Stephen Boyd. “OSQP: An Operator Splitting Solver for Quadratic Programs.” Mathematical Programming Computation 12, no. 4 (December 2020): 637–72. https://doi.org/10.1007/s12532-020-00179-2.

上一篇Python 装饰器

下一篇相机是如何对焦的

本文作者：凌晗

本文链接：https://www.cnblogs.com/dawnlh/p/17615770.html

posted @ 2023-08-09 00:13 凌晗阅读(1413) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

凌晗

二次规划问题和常见求解框架