浅谈流形
流形是什么?
看了这么多答案,我觉得流形就是一种符合某种规范的几何体。某种规范可以简单的理解为这种几何体的的每个局部都是符合欧式几何体特征的。我觉得流形就是为了解决非欧几何体问题的,把非欧几何体映射成多个欧式几何体的组合,这样我就可以用上以前在欧式几何中的各种数学工具了。有一个对于manifold非常好的解释,manifold=many fold 多个面拼接而成的东西。
那么这个跟深度学习有什么关系,为什么会在深度学习中频繁的出现“嵌入在高维空间的低维流形”这样的词。
机器学习或者深度学习学习的是什么?学习的是一种模式。那么这种模式用什么来表达呢?概率是一种表达方式,万有引力定律这样的物理公式也是一种模式。如果模式能够形象化的话,那会是什么样子的呢?万有引力定律学习出了椭圆轨道。但是这是非常简单的一种情况。如果我们学习的模式是高维空间的一种几何体,无法用我们在三维空间中的立方体,球体这样的几何形体来描述,样的那么我们应该如何描述这样的几何体,这个时候就需要用到“流形”的概念了。
另外,“流形”既然是一个几何体,那么就占据着一部分空间。所以也可以把流形看成一个空间,扭曲的空间。
好,我们现在知道我们现在要学习的模式可以用“流形”这个概念。
那么什么是“嵌入在高维空间中的低维流形”呢?
有这么几个例子:
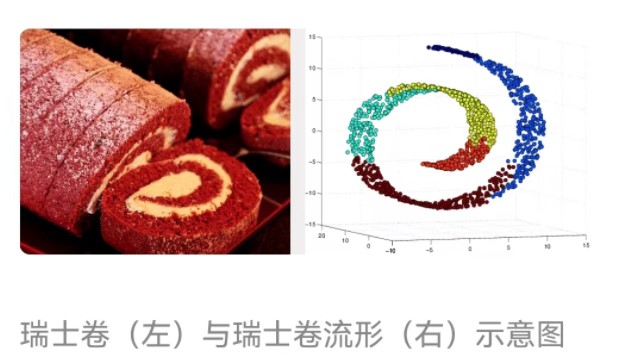
第一个例子——瑞士卷
瑞士卷本质是二维的流形在三维的一个嵌入。
瑞士卷原本是一个平面(二维的几何体),但是通过扭曲的操作它变成了一个三维的几何体。
或者说它从二维几何体升级到了三维的几何体。我们把这种维度升级的现象叫做嵌入。
第二个例子——身份证号
其实身份证号码只要能够区别不同的人就可以了。
其实只要10位数字(x000000000)足够表达全目前全中国的人口(甚至全世界的人口)
但是我们现在却用了18位数字来表达(因为我们需要用一些位数来表达省份区域等等信息)。所以这个可以认为是本质上10维的流形嵌入到18维空间的例子。
第三个例子——平面上的圆
对于一个圆,我们如何表达他们,如果是在直角坐标系中,我们可能会用两个数字(一个坐标)来表达圆上的每个点。但是其实除了这个圆上的坐标以外,其他地方的点都是冗余的。换句话说为了盛一粒米,我们用了一个米缸的感觉。有没有不冗余的方法呢?用极坐标。极坐标虽然也是有两个量,一个是角度一个是圆的半径,但是之前我们已经说了要表达的是圆也就是角度始终是365度,这个是一个定值。那么也用半径这一个自由变量就行了。也就是说去除冗余,平面圆其实是一个一维的流形在二维空间的一个嵌入。
同理球体也是,它只有两个自由度,它是二维的流形在三维空间的嵌入。
第四个例子——人脸

这里的图片来自同一张人脸(好吧,其实是人脸模型),每张图片是 64×64 的灰度图,如果把位图按照列(或行)拼起来,就可以得到一个 4096 维的向量,这样一来,每一张图片就可以看成是 4096 维欧氏空间中的一个点。很显然,并不是 4096 维空间中任意一个点都可以对应于一张人脸图片的,这就类似于球面的情形,我们可以假定所有可以是人脸的 4096 维向量实际上分布在一个 d 维 (d < 4096) 的子空间中。而特定到 Isomap 的人脸这个例子,实际上我们知道所有的 698 张图片是拍自同一个人脸(模型),不过是在不同的 pose 和光照下拍摄的,如果把 pose (上下和左右)当作两个自由度,而光照当作一个自由度,那么这些图片实际只有三个自由度,换句话说,存在一个类似于球面一样的参数方程(当然,解析式是没法写出来的),给定一组参数(也就是上下、左右的 pose 和光照这三个值),就可以生成出对应的 4096 维的坐标来。换句话说,这是一个嵌入在 4096 维欧氏空间中的一个 3 维流形。 实际上,上面的那张图就是 Isomap 将这个数据集从 4096 维映射到 3 维空间中,并显示了其中 2 维的结果,图中的小点就是每个人脸在这个二维空间中对应的坐标位置,其中一些标红圈的点被选出来,并在旁边画上了该点对应的原始图片,可以很直观地看出这两个维度正好对应了 pose 的两个自由度平滑变化的结果。 就我目前所知,把流形引入到机器学习领域来主要有两种用途:一是将原来在欧氏空间中适用的算法加以改造,使得它工作在流形上,直接或间接地对流形的结构和性质加以利用;二是直接分析流形的结构,并试图将其映射到一个欧氏空间中,再在得到的结果上运用以前适用于欧氏空间的算法来进行学习。 这里 Isomap 正巧是一个非常典型的例子,因为它实际上是通过“改造一种原本适用于欧氏空间的算法”,达到了“将流形映射到一个欧氏空间”的目的。 Isomap 所改造的这个方法叫做 Multidimensional Scaling (MDS) ,MDS 是一种降维方法,它的目的就是使得降维之后的点两两之间的距离尽量不变(也就是和在原是空间中对应的两个点之间的距离要差不多)。只是 MDS 是针对欧氏空间设计的,对于距离的计算也是使用欧氏距离来完成的。如果数据分布在一个流形上的话,欧氏距离就不适用了
你会发现我们在现实中直接获得的数据都是低维流形在高维空间的嵌入了。
这也是流形学习的一个观点,我们从现实世界观察到自然数据其实都是“低维流形在高维空间的嵌入”
同理我们现在深度学习用的RGB表征其实也是一种“低维流形在高维空间的嵌入”
现在我们已经知道,我们手上的数据其实是“低维流形在高维空间中的嵌入”,那么接下来呢?
接下来我们讨论的问题是“距离”
我们知道“分类”是机器学习最重要的任务,而分类很大程度上是基于“距离”这个概念的。距离近样本我们认为他们是一类,距离远的样本我们认为他们不是一类。
而过去我们计算距离就是直接用的欧式距离。这个在三维空间里是没啥问题的,但是一旦不能想当然的推广到高维空间。
比如我们要测量地球仪上北京到广州的距离,我肯定是拿一个尺子贴着球体表面去测量,如果我要拿一根棍从北京插进去再从广州穿出来这样测量,你肯定会认为我疯了。而事实上我们再高维空间用欧式距离度量两个点的距离就是这样的。
那么应该怎么测量,这里就要引入一个新的概念“测地线”。你不用问测地线的具体定义是什么,问就是一堆公式。简单来说测地线就是在流形中衡量两个点之间的最短距离。
还是以瑞士卷为例子,两个点之间的距离应该是红色线的距离而不是蓝色线的距离。
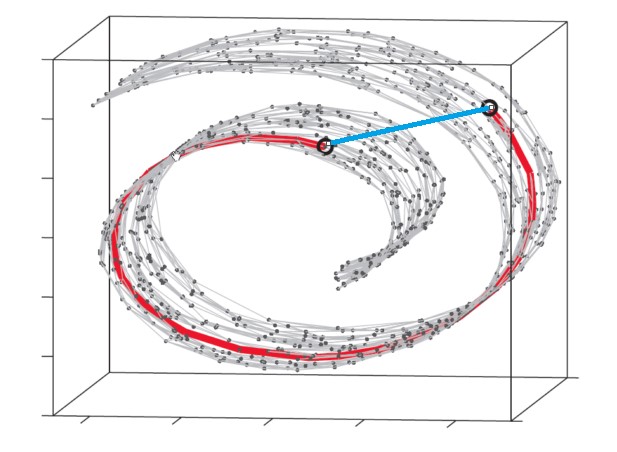
那么当我们知道我们机器学习学习对象是流形之后,是不是我们之前计算距离的方式都要改变呢?这个是一个方案。把过去适用于欧式空间的算法加以改造,使他们适合在流形上也能正常的工作。还有一个方案就是降维,通过降维把流形的维度降到不那么高的程度,使欧氏距离也能近似的表达流形上的距离。
这就是为什么在很多文章中,都要考虑降维,一方面是出于计算量的考量。另一方面就是可以让基于欧式距离推导的算法能够更好的工作。
参考文献:
求简要介绍一下流形学习的基本思想? - 麋路的回答 - 知乎 https://www.zhihu.com/question/24015486/answer/194284643
怎么形象理解embedding这个概念? - 刘斯坦的回答 - 知乎 https://www.zhihu.com/question/38002635/answer/1382442522
浅谈流形学习 来自 https://blog.pluskid.org/archives/533



