0098-验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

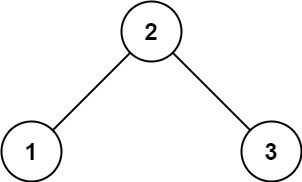
输入：root = [2,1,3]
输出：true
示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/validate-binary-search-tree

参考：

python

# 0098.验证二叉搜索树

# 递归-压缩数组-中序看是否升序数组
class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        cadidate_list = []

        def _traversal(root):
            nonlocal cadidate_list
            if not root:
                return
            _traversal(root.left)
            cadidate_list.append(root.val)
            _traversal(root.right)

        _traversal(root)

        for i in range(1, len(cadidate_list)):
            if cadidate_list[i] <= cadidate_list[i-1]:
                return False
        return True


# 递归-标准中序-中序
class Solution2:
    def isValidBST(self, root: TreeNode) -> bool:
        curMax = -float("INF")
        def travel(root):
            nonlocal curMax
            if not root:
                return True
            isLeftValid = travel(root.left)

            if curMax < root.val:
                curMax = root.val
            else:
                return False

            isRightValid = travel(root.right)

            return isLeftValid and isRightValid
        return travel(root)

# 迭代法-中序遍历
class Solution3:
    def isValidBST(self, root: TreeNode) -> bool:
        stack = []
        cur = root
        pre = None

        while cur or stack:
            if cur: # 先遍历至最左节点
                stack.append(cur)
                cur = cur.left
            else: # 依次处理栈顶节点
                cur = stack.pop()
                if pre and cur.val <= pre.val:
                    return False
                pre = cur
                cur = cur.right

        return True

golang

package binaryTree

import "math"

// 递归-中序数组比较是否升序
func isValidBst(root *TreeNode) bool {
	res := []int{}
	var traversal func(node *TreeNode)
	traversal = func(node *TreeNode) {
		if node == nil {
			return
		}
		traversal(node.Left)
		res = append(res, node.Val)
		traversal(node.Right)
	}
	traversal(root)

	for i:=1;i<len(res);i++ {
		if res[i] <= res[i-1] {
			return false
		}
	}

	return true
}

// 递归-中序遍历-标准中序
func isVaildBST2(root *TreeNode) bool {
	var pre *TreeNode

	var traversal func(node *TreeNode) bool
	traversal = func(node *TreeNode) bool {
		if node == nil {
			return true
		}
		isLeftVaild := traversal(root.Left)

		if pre != nil && node.Val <= pre.Val {
			return false
		}
		pre = node

		isRightVaild := traversal(root.Right)
		return isLeftVaild && isRightVaild
	}
	return traversal(root)
}

// 迭代法-中序遍历
func isValidBST3(root *TreeNode) bool {
	stack := []*TreeNode{}
	Max := math.MinInt32

	for len(stack) > 0 || root != nil {
		for root != nil {
			stack = append(stack, root)
			root = root.Left
		}
		root = stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		if root.Val <= Max {
			return false
		}
		Max = root.Val
		root = root.Right
	}
	return true
}