求给定字符串的既是非空前缀又是非空后缀的最长子串

问题：求给定字符串的既是非空真前缀又是非空真后缀的最长子串（后面简称match串），示例如下：

真前缀表示不包括字符串自身的其余前缀子串，真后缀同理

输入str = “abbca"，输出 match = ”a"

输入str = "GTGTG"，输出 match = "GTG"

输入"a", 输出“”

思路：KMP算法

要点：

1、定义next数组，next[i]表示长度为i的str前缀子串s[0, i]的match长度，则str的match = str.substr(0, next[str.length]);

     长度为0和1的str子串match = "", next[0] = next[1] = 0;

2、定义2个指针变量i和j，i不断向右移动以扩大子串的大小，j指向可能的（说可能是因为也许这个过程中还没找到相应的match串，那么它指向的位置就不是）前缀match串最后一个字符的索引位置。

如下图过程说明：

第一轮：

 初始状态，j = 0, i = 1, str[0, i + 1] = "GT"

因为 str[i] != str[j], 故 next[len(str[0, i + 1])] = next[i + 1] = next[2] = 0

i向右移动一位，++i

--------------------------------------------------------------------------------------

第二轮：

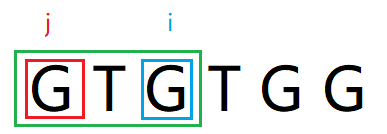
 j = 0,  i = 2,  str[0, i + 1] = "GTG"

因为 str[i] == str[j], 故此时的j表示match串“G”的最后一个字符索引位置0， 把j向右移动一位，++j，

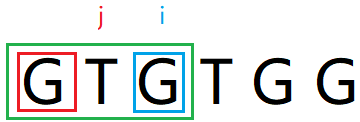
此时j既能表示match串的长度，同时也表示i要比较的下一个j的位置

next[i + 1] = next[3] = j = 1

 i向右移动一位，++i

--------------------------------------------------------------------------------------

第三轮：

 

j = 1, i = 3, str[0, i + 1] = str[0, 4] = "GTGT"

str[i] == str[j] , 则 ++j,   j = 2

 

 next[i + 1] = next[4] = j = 2

 i向右移动一位，++i

--------------------------------------------------------------------------------------

第四轮：

 

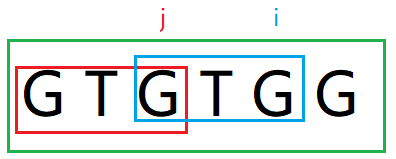
j = 2, i = 4, str[0, i + 1] = str[0, 5] = "GTGTG"

str[i] == str[j] , 则 ++j,   j = 3

 

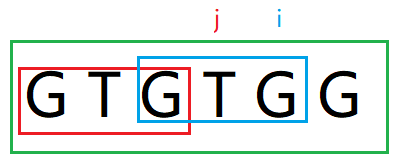
 next[i + 1] = next[5] = j = 3

 i向右移动一位，++i

--------------------------------------------------------------------------------------

第五轮：

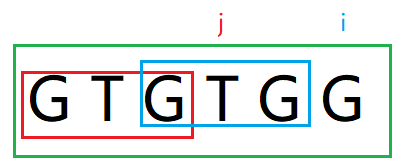
 j = 3, i = 5, str[0, i + 1] = str[0, 6] = "GTGTGG"

 str[i] != str[j] , 这时候，next[6]无法在next[5]基础上+1获得了，next[5] + 1一定会使next[6]变大，即match串变长，显然，当前next[6] <= next[5]，那怎么求next[6]呢？

先看看暴力求法图解：

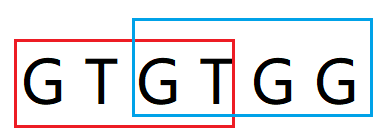
 红框str[0, j] = "GTGT" 不等于 蓝框str[j -1,  i] = "GTGG",  match串长度-1

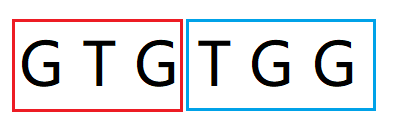
  红框str[0, j-1] = "GTG" 不等于 蓝框str[j,  i] = "TGG",  match串长度-1

   红框str[0, j-2] = "GT" 不等于 蓝框str[j+1,  i] = "GG",  match串长度-1

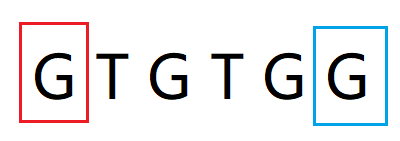
 红框str[0, j-3] = "G" 等于 蓝框str[j+2,  i] = "G",  match串长度为1，match串 = "G"

 这样求解效率肯定很差，每次都要弄两个指针(pi, sj)分别来收缩前缀子串和后缀子串的结束位置边界和起始位置边界，再判断str[0, pi]与str[sj, i]是否相等。

 优化：

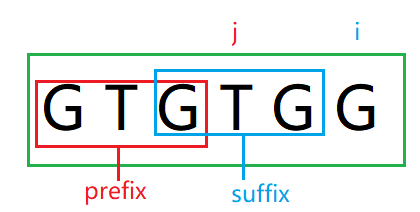
 令原字符串为A = "GTGTG"，i向右移动一位得到新字符串B = A + "G",  A ∈ str, B ∈ str

因为str[j] = "T", str[i] = "G", str[j] != str[i]， 所以 next[6] <= next[5], 即 next[6] <= 3, 因此B的match串的范围必然落在str[0, 3]之间，即prefix=“GTG”，

由于suffix = prefix = "GTG"且suffix的下一个字符就是str[i],  我们可以利用suffix简化计算，即把计算B的match转换为计算C＝suffix + str[i] = "GTGG"的match串，

对于C中的str[j]的索引可由j = next[j] 计算得到， 在A串中，j = 3， next[3] = 1，故 j = next[3] = 1，其实就是suffix中的 j 在prefix中j的位置，这里str[3] = str[1] = "T", 它们相同，

但此时依然存在str[i] != str[j] ，同理继续转换：

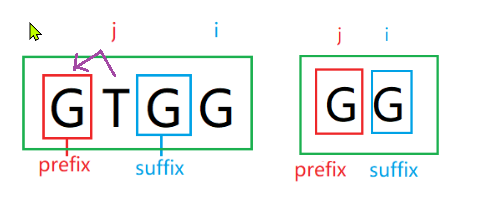
 j = next[j] = next[1] = 0,  str[i] == 'G' = =str[j] = = str[0]，由于j = 0, 已经没有办法转换了，此时 ++j,  next[6] = j  = 1, 结束。

我们利用prefix == suffix 这种特点相对高效的解决了问题。

class Solution {
public:
    string longestPrefix(string s) {
        int n = s.size();
        std::vector<int> next(n + 1, 0);
        for (int i = 1, j = 0; i < n; ++i) {
            while (j != 0 && s[j] != s[i])
            {
                j = next[j]; 
            }

            if (s[j] == s[i]) {
                ++j;
            }
            next[i+1] = j;
        }
        return s.substr(0, next[n]);
    }
};