普通克里金算法学习笔记

简介：

 Kriging是一组统计技术，用来将随机场的值(例如，地形的高程，z，作为地理位置的函数)从其在附近位置的观测值中插值到一个未观测到的位置。

令\((x,y)\)为某一空间数据点的坐标，\(Z(x,y)\)表示其值，对于某个点\((x_0,y_0)\)的值记为\(z_0=Z(x_0, y_0)\)，则克里金插值公式如下：

\(\hat{z}_0=\sum_{i=1}^n\omega_iz_i\)

\(\hat{z}_0\)表示点\((x_0,y_0)\)处的估计值，它由该点附近n个点的观测值\(z_i\)(1<=i<=n)与相对该点\((x_0,y_0)\)的权重系数\(\omega_i\)的线性组合决定。

 一、数学原理

1、假设条件

（1）数学期望未知但是一个恒定的值\(E[Z(x,y)]={\mu}\);

（2）\(Z(x,y)\)的变异函数是已知的\({\gamma}(x, y)_{ij} = E[(z_i - z_j)^2]\).

解释：普通克里金（Ordinary Kriging)的假设条件为：空间属性z是均一的，对空间任意一点（x,y)都有相同的期望

因此可以据此得出任意一点\((x,y)\)的都由区域均值\(\mu\)和该点的随机偏差\(R(x,y)\)组成，即\(Z(x,y)=E[Z(x,y)]+R(x,y)]=\mu+R(x,y)\)

\(R(x,y)=Z(x,y)-\mu\)，而方差\(\sigma^2=Var(Z(x,y))=E[(Z(x,y)-\mu)^2]=E[R(x,y)^2]\)

所以随机偏差的方差也是常数\(\sigma^2\)，\(Var[R(x,y)]=\sigma^2\)

下文中绝大多数为方便起见都将\(Z(x,y)\)记作\(z_i\)，\(R(x,y)\)记作\(r_i\)

 

2、无偏估计条件

普通克里金的权重\(\omega\)需要满足无偏估计，即 

\(\sum_{i=1}^{n}{\omega_i}=1\)

证明如下：

无偏估计条件是 \(E(\hat{z_{0}}-z_{0})=0\), 代入\(\hat{z_{0}}=\sum_{i=1}^{n}{\omega_iz_i}\)得：

\(E(\sum_{i=1}^{n}{\omega_iz_i}-z_0)=0\)

因为对任意的z都存在E[z] = μ, 则有

\(μ\sum_{i=1}^{n}{\omega_i}-μ=0\)

约去μ得证

\(\sum_{i=1}^{n}{\omega_i}=1\)

 

3、半方差

先复习下数学期望、方差、协方差公式之间的关系：

设X、Y是随机变量，C、a、b均为常数,记\(D(X)\)和\(D(Y)\)分别表示各自的方差，\(E(X)\)和\(E(Y)\)分别表示各自的数学期望，\(Cov(X,Y)\)表示X与Y的协方差，则有如下关系：

\(E(C)=C\)

\(E(CX)=CE(X)\)

\(E(CX)=CE(X)\)

\(E(X+Y)=E(X)+E(Y)\)

当X和Y相互独立时，\(E(XY)=E(X)E(Y)\)

\(D(X+Y)=D(X)+D(Y)+2Cov(X,Y)\)

\(D(X-Y)=D(X)+D(Y)-2Cov(X,Y)\)

\(Cov(X,Y)=E(XY)-E(X)E(Y)\)

\(Cov(X,Y)=Cov(Y,X)\)

\(Cov(aX,bY)=ab{\cdot}Cov(X,Y)\)

\(Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(X_2,Y)\)

\(Cov(X+a,Y+b)=Cov(X,Y)\)

\(Cov(X,X)=D(X)\)

\(Cov(Y,Y)=D(Y)\)

 

半方差定义：\(r_{ij}=\sigma^2-Cov(z_i,z_j)\)，\(\sigma^2\)表示方差；其等价形式为\(r_{ij}=\frac{1}{2}E[(z_i-z_j)^2]\)，证明如下：

由上文知\(r_i=z_i-\mu\)，则\(z_i-z_j=r_i-r_j\)，从而

\(r_{ij}=\frac{1}{2}E[(r_i-r_j)^2]\)

=\(\frac{1}{2}E[r_{i}^2-2r_ir_j+r_j^2]\)

=\(\frac{1}{2}E[r_{i}^2]-E[r_ir_j]+\frac{1}{2}E[r_j^2]\)

又\(E[r_i^2]=E[r_j^2]=E[(z_i-\mu)^2]=Var(z_i)=\sigma^2\)

\(E[r_ir_j]=E[(z_i-\mu)(z_j-\mu)]=Cov(z_i,z_j)\)

于是有

\(r_{ij}=\frac{1}{2}E[(z_i-z_j)^2]\)

\(=\frac{1}{2}E[r_i^2]+\frac{1}{2}E[r_j^2]-E[r_ir_j]\)

\(=\frac{1}{2}\sigma^2+\frac{1}{2}\sigma^2-Cov(z_i,z_j)\)

\(=\sigma^2-Cov(z_i,z_j)\)

4、优化目标函数

克里金误差（kriging variance or kriging error)给出如下：

\(\sigma_k^2(z_0):=Var(\hat{z_0}-z_0)\)

推导\(\sigma_k^2(z_0):=Var(\hat{z_0}-z_0)\)

=\(Var(\hat{z_0})+Var(z_0)-2{\cdot}Cov(\hat{z_0}-z_0)\)

又\(Var(\hat{z_0})=Var(\sum_{i=1}^n\omega_iz_i)\)

\(=Cov(\sum_{i=1}^n\omega_iz_i,\sum_{i=1}^n\omega_iz_i)\)

\(=Cov(\sum_{i=1}^n\omega_iz_i,\sum_{j=1}^n\omega_jz_j)\)(第二个参数中的i用j替换)

\(=\sum_{i=1}^n\omega_i\sum_{j=1}^n\omega_j{\cdot}Cov(z_i,z_j)\)

\(=\sum_{i=1}^n\sum_{j=1}^n\omega_i\omega_j{\cdot}Cov(z_i,z_j)\)

则有：\(\sigma_k^2(z_0):=Var(\hat{z_0}-z_0)\)

=\(\sum_{i=1}^n\sum_{j=1}^n\omega_i\omega_j{\cdot}Cov(z_i,z_j)+Cov(z_0,z_0)-2\sum_{i=1}^n\omega_i{\cdot}Cov(z_i,z_0)\)

由上文知:\(Cov(z_i,z_j)=\sigma^2-r_{ij}\)，\(\sum_{i=1}^n=1\)

从而\(\sigma_k^2(z_0):=\sum_{i=1}^n\sum_{j=1}^n\omega_i\omega_j(\sigma^2-r_{ij})+(\sigma^2-r_{00})-2\sum_{i=1}^nw_i(\sigma^2-r_{i0})\)

=\(\sum_{i=1}^n\sum_{j=1}^nw_iw_j(\sigma^2)-\sum_{i=1}^n\sum_{j=1}^nw_iw_j(r_{ij})+(\sigma^2-r_{00})-2\sum_{i=1}^nw_i(\sigma^2)+2\sum_{i=1}^nw_i(r_{i0})\)

=\(\sigma^2-\sum_{i=1}^n\sum_{j=1}^nw_iw_j(r_{ij})+\sigma^2-r_{00}-2\sigma^2+2\sum_{i=1}^nw_i(r_{i0})\)

=\(2\sum_{i=1}^nw_i(r_{i0})-\sum_{i=1}^n\sum_{j=1}^nw_iw_j(r_{ij})-r_{00}\)

接下来寻找使\(\sigma_k^2(z_0)\)最小的一组\(w_i\)，应用拉格朗日乘数法求解。

回顾拉格朗日乘数法知识：

设给定二元函数z=ƒ(x,y)和附加条件φ(x,y)=0，为寻找z=ƒ(x,y)在附加条件下的极值点，先做拉格朗日函数 ，其中λ为参数。

令F(x,y,λ)对x和y和λ的一阶偏导数等于零，即

F'x=ƒ'x(x,y)+λφ'x(x,y)=0 [1]

F'y=ƒ'y(x,y)+λφ'y(x,y)=0

F'λ=φ(x,y)=0

由上述方程组解出x,y及λ，如此求得的(x,y)，就是函数z=ƒ(x,y)在附加条件φ(x,y)=0下的可能极值点。

若这样的点只有一个，由实际问题可直接确定此即所求的点。

为使\(\sigma_k^2(z_0)\)最小，构造拉格朗日函数\(J=F(w_0,w_1,...,w_n,\lambda)=f(w_0,w_1,...,w_n)+\lambda\phi(\sum_{i=1}^n-1)=\sigma_k^2(z_0)+\lambda\phi(\sum_{i=1}^n-1)\)

其中\(\lambda\phi(\sum_{i=1}^n-1)\)是约束条件，\(\lambda\)是拉格朗日乘数。

将\(J\)对\(\omega_i\)求偏导并令其值为0，即\(\frac{\partial J}{\partial \omega_i}= 0;i=1,2,\cdots,n\)

求解过程暂略，最终会得到如下的矩阵方程：

\(\begin{bmatrix}w_1\\ w_2\\ ...\\w_n\\ k\lambda\\\end{bmatrix}=\begin{bmatrix} r_{11}&r_{12}&...&r_{1n}&1\\ r_{21}&r_{22}&...&r_{2n}&1\\ ...&...&...&...&...\\ r_{n1}&r_{n2}&...&r_{nn}&1\\ 1& 1& ...& 1 & 0 \end{bmatrix}^T\begin{bmatrix} r_{1o}\\ r_{2o}\\ ...\\ r_{no}\\ 1\\ \end{bmatrix}\)

向量\(W=\begin{bmatrix}w_1\\ w_2\\ ...\\w_n\\ k\lambda\\\end{bmatrix}\)中的\(w\)就是用于最后计算预测值的权重。

5、半变异函数模型拟合

对于4中的求解需要先拟合半方差函数以获得半变异模型，然后再根据半变异模型获取满足空间自相关的一定范围（range)内的观察值，运用这些观测值结合4来计算最终的预测值。

 

 

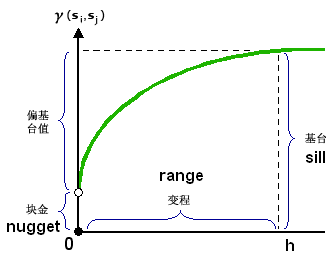
 半方差的计算方式如下：计算预测点附近N个观测值两两之间的空间位置欧几里德距离h和值误差（均方误差或半方差等）r，然后绘制r关于h的散点图，一般情况下，如果地理属性之间存在空间自相关，那么

r会随着h的增大逐渐增大，h大到一定程度（range)后r会收敛于某个值（sill)，表示超过h这个距离后其他的观测值对预测值的自相关性已经可以忽略不计了。此时就应该用range范围内的观测数据去计算预测值。

几种常见的函数模型如下：

 

 

 

 

 

 

 

 

 

 

 

 

 

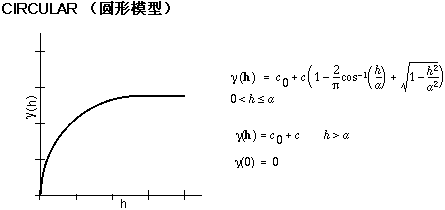
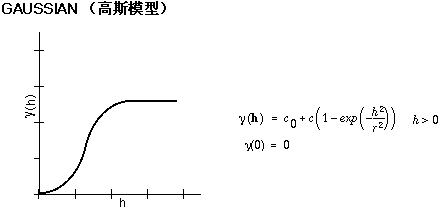
 线性模型用的应该比较少，线性模型可以用线性最小二乘法拟合以获得函数参数，对于球体、指数、高斯等其他曲线模型可以用非线性最小二乘法拟合以获得函数参数。有关最小二乘法介绍可参考最小二乘法应用：用直线或曲线模型拟合散点 - DavidXu2014 - 博客园 (cnblogs.com)

个人推测实际应用克里金插值的散点数量如果比较大应该不是把所有的点都拟合一次来进行预测，观察ArcMap的克里金插值是设置的椭圆半径范围内的最大最小相邻元素数目，所以应该就是用预测值附近选取的N个点拟合半变异模型，获得nugget、range、sill参数，然后用range范围内的点估计预测值。

用线性模型拟合散点：

 

用球体模型拟合散点：

 

 

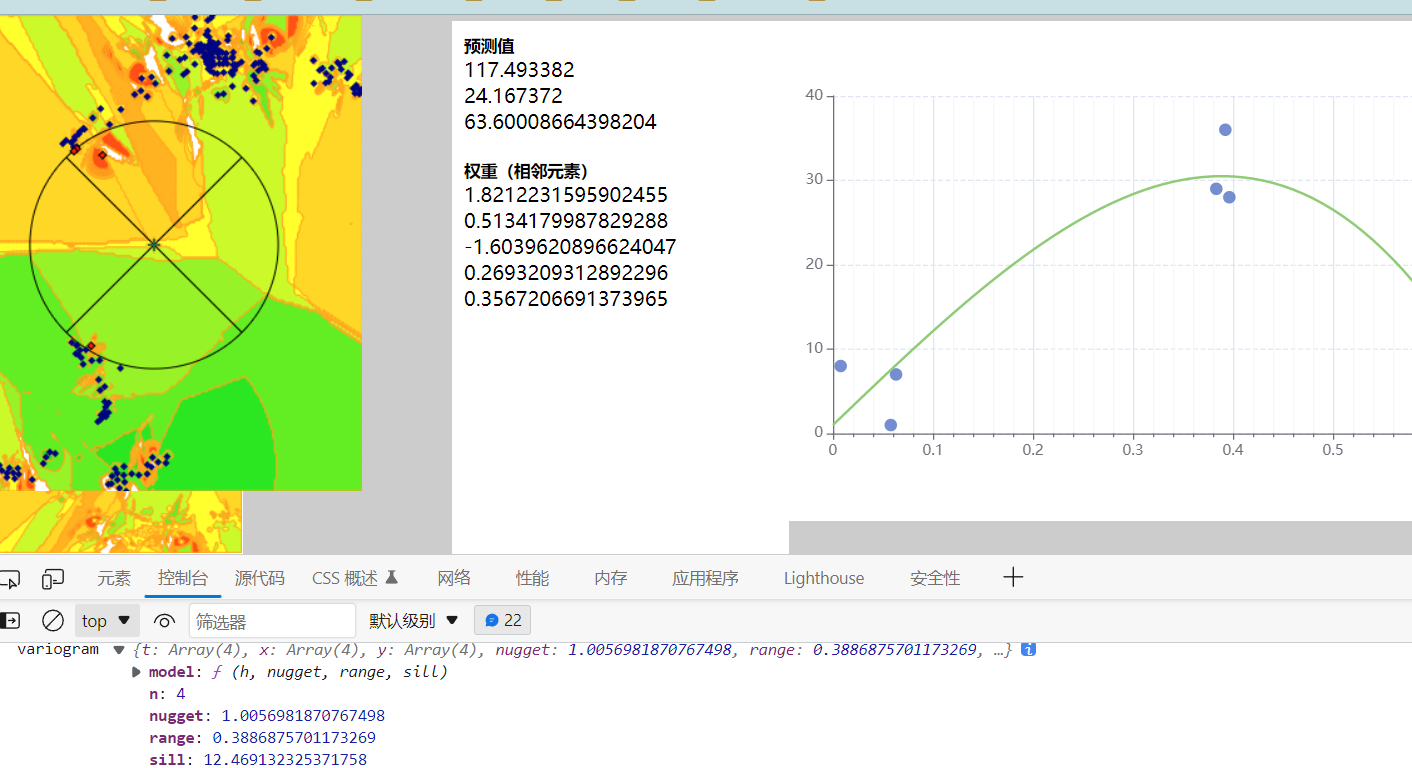
注释：数据如果不存在空间自相关的这种特性或不满足克里金算法的假设条件，模型拟合效果可能很差，最终效果就不理想。

 

References：

http://wiki.gis.com/wiki/index.php/Kriging#Ordinary_kriging_equation

https://desktop.arcgis.com/zh-cn/arcmap/10.3/tools/3d-analyst-toolbox/how-kriging-works.htm

https://xg1990.com/blog/en/archives/222