1、决策树的构造
createBranch伪代码:
检测数据集中的每个子项是否属于同一分类:
IF SO RETURN 类标签
ELSE
寻找划分数据集的最好特征
划分数据集
创建分支节点
FOR 每个划分的子集
调用函数createBranch并增加返回结果到分支节点中
RETURN 分支节点
划分数据集的大原则:将无序的数据变的更加有序。在划分数据集之前之后信息发生的变化称为信息增益,获得信息增益最高的特征就是最好的选择
熵定义为信息的期望值。熵越大越离散。
计算给定数据集的香农熵
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt
2.决策树的构造算法
ID3算法
ID3算法是一种分类决策树算法。他通过一系列的规则,将数据最后分类成决策树的形式。分类的根据是用到了熵这个概念。熵在物理这门学科中就已经出现过,表示是一个物质的稳定度,在这里就是分类的纯度的一个概念。公式为:
C4.5算法
C4.5与ID3在核心的算法是一样的,但是有一点所采用的办法是不同的,C4.5采用了信息增益率作为划分的根据,克服了ID3算法中采用信息增益划分导致属性选择偏向取值多的属性。信息增益率的公式为:
分母的位置是分裂因子,他的计算公式为:
CART算法
CART算法对于属性的值采用的是基于Gini系数值的方式做比较,gini某个属性的某次值的划分的gini指数的值为:


微信公众号: 架构师日常笔记 欢迎关注!


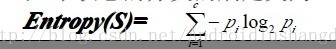
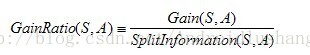
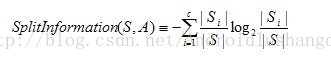

 浙公网安备 33010602011771号
浙公网安备 33010602011771号