浅谈C++之冒泡排序、希尔排序、快速排序、插入排序、堆排序、基数排序性能对比分析(好戏在后面,有图有真相)
最近一段时间去武汉参加了N多笔试,在几次试题中都出现了排序。偏偏出现了我没怎么看的插入排序,弄得我好是纠结。趁回学校的机会把这几个不是很复杂的排序重新复习了一下,借此比较了一下他们的效率。让我有点以外的是在数据量达到1W~10W之间,希尔排序竟然比快速排序效率还要高。贴上完整代码!
冒泡排序
1 //冒泡排序
2 //////////////////////////////////////////////////////////////////////////
3 void BubleSort(int a[],int n)
4 {
5 int temp;
6 bool flag=false;
7 for (int i=0;i<n;i++)
8 {
9 flag=true;
10 for (int j=0;j<n-i-1;j++)
11 {
12 if(a[j]>a[j+1])
13 {
14 temp=a[j];
15 a[j]=a[j+1];
16 a[j+1]=temp;
17 flag=false;
18 }
19 }
20 if(flag) break;
21 }
22 }
冒泡排序的时间复杂度为O(n²),在数据比较小的情况下各个算法效率差不多。
希尔排序:
//希尔排序
///////////////////////////////////////////
void ShellSort(int a[],int n)
{
int d=n;
int temp;
while(d>1)
{
d=(d+1)/2;
for(int i=0;i<n-d;i++)
if (a[i]>a[i+d])
{
temp=a[i];
a[i]=a[i+d];
a[i+d]=temp;
}
}
}
以前竟然没有发现,希尔排序如此短小精悍的代码。其效率很多时候并不输给快速排序其时间复杂度为O(nlogn)。
快速排序:
1 //快速排序
2 ///////////////////////////////////////
3 void Swap(int &a,int &b)
4 {
5 int temp;
6 temp=a;
7 a=b;
8 b=temp;
9 }
10
11 int Partition(int a[],int p,int r)
12 {
13 int i=p;
14 int j=r+1;
15 int x=a[p];
16 while (true)
17 {
18 while(a[++i]<x&&i<r);
19 while(a[--j]>x);
20 if (i>=j)break;
21 Swap(a[j],a[i]);
22
23 }
24 a[p]=a[j];
25 a[j]=x;
26 return j;
27 }
28
29 void QuickSort(int a[],int p,int r)
30 {
31 if (p<r)
32 {
33 int q=Partition(a,p,r);
34 QuickSort(a,p,q-1);
35 QuickSort(a,q+1,r);
36 }
37 }
正如其名快速排序,其效率也是比较高的,时间复杂度为O(nlogn)。其算法思想是每次确定一个基准值的位置,也就是函数int Partition(int a[],int p,int r)的作用。然后通过递归不断地确定基准值两边的子数组的基准值的位置,直到数组变得有序。难点还是递归的理解!
插入排序:
1 //插入排序
2 //////////////////////////////////////////////////////////////////
3 void Insert(int *a,int n)
4 {
5 int i=n-1;
6 int key=a[n];//需要插入的元素
7 while ((i>=0)&&(key<a[i]))
8 {
9 a[i+1]=a[i]; //比key大的元素往后一个位置,空出插入key的位置
10 i--;
11 }
12 a[i+1]=key;//找到位置插入元素
13 return;
14 }
15
16 //由于递归的原因数太大了栈可能会溢出
17 void InsertionSort(int *a,int n)
18 {
19 if (n>0)
20 {
21 InsertionSort(a,n-1);
22 Insert(a,n);
23 }
24 else return;
25 }
算法效率和冒泡排序相差无几,时间复杂度为O(n²)。这里要注意的问题是由于不断地递归,栈的不断开辟如果数据太大可能会导致栈溢出而不能得到结果。
堆排序:
1 //堆排序
2 ////////////////////////////////////////////////////////////////////////////
3 int Parent(int i)
4 {
5 return i/2;
6 }
7 int Left(int i)
8 {
9 return 2*i;
10 }
11 int Right(int i)
12 {
13 return 2*i+1;
14 }
15
16 //把以第i个节点给子树的根的子树调整为堆
17 void MaxHeap(int *a,int i,int length)
18 {
19 int L=Left(i);
20 int R=Right(i);
21 int temp;
22 int largest; //记录子树最大值的下表,值可能为根节点下标、左子树下表、右子树下标
23 if (L<=length&&a[L-1]>a[i-1]) //length是递归返回的条件
24 {
25 largest=L;
26 }
27 else largest=i;
28 if (R<=length&&a[R-1]>a[largest-1]) //length是递归返回的条件
29 largest=R;
30 if (largest!=i)
31 {
32 temp=a[i-1];
33 a[i-1]=a[largest-1];
34 a[largest-1]=temp;
35 MaxHeap(a,largest,length);
36 }
37 }
38
39 void BuildMaxHeap(int *a,int length)
40 {
41
42 for (int i=length/2;i>=1;i--)
43 MaxHeap(a,i,length);
44 }
45
46 void HeapSort(int *a,int length)
47 {
48 BuildMaxHeap(a,length);
49 for (int i=length;i>0;i--)
50 {
51 int temp;
52 temp=a[i-1];
53 a[i-1]=a[0];
54 a[0]=temp;
55 length-=1;
56 MaxHeap(a,1,length);
57 }
58 }
通过使用大根堆来排序,排序过程中主要的动作就是堆的调整。每次把堆的根节点存入到堆的后面,然后把最后一个节点交换到根节点的位置,然后又调整为新的堆。这样不断重复这个步骤就能把把一个数组排列的有序,时间复杂度为O(nlogn)。
最后一种是比较特别的基数排序(属于分配式排序,前几种属于比较性排序)又称“桶子法”:
基本思想是通过键值的部分信息分配到某些桶中,藉此达到排序的作用,基数排序属于稳定的排序,其时间复杂度为O(nlog(r)m),r为所采取的的基数,m为堆的个数,在某些情况下基数排序法的效率比其他比较性排序效率要高。
1 //基数排序
2 /////////////////////////////////////////////////
3 int GetMaxTimes(int *a,int n)
4 {
5 int max=a[0];
6 int count=0;
7 for (int i=1;i<n;i++)
8 {
9 if(a[i]>max)
10 max=a[i];
11 }
12 while(max)
13 {
14 max=max/10;
15 count++;
16 }
17 return count;
18 }
19
20 void InitialArray(int *a,int n)
21 {
22 for (int i=0;i<n;i++)
23 a[i]=0;
24 }
25
26 // void InitialArray1(int a[][],int m,int n)
27 // {
28 // for (int i=0;i<m;i++)
29 // for (int j=0;j<n;j++)
30 // a[i][j]=0;
31 // }
32
33 void RadixSort(int *a,int n)
34 {
35 int buckets[10][10000]={0};
36 int times=GetMaxTimes(a,n);
37 int index,temp;
38 int record[10]={0};
39 for (int i=0;i<times;i++)
40 {
41 int count=0;
42 temp=pow(10,i);//index=(a[j]/temp)%10;用来从低位到高位分离
43 for (int j=0;j<n;j++)
44 {
45 index=(a[j]/temp)%10;
46 buckets[index][record[index]++]=a[j];
47 }
48 //把桶中的数据按顺序还原到原数组中
49 for(int k=0;k<10;k++)
50 for (int m=0;m<100000;m++)
51 {
52 if(buckets[k][m]==0)break;
53 else
54 {
55 a[count++]=buckets[k][m];
56 //cout<<buckets[k][m]<<" ";
57 }
58 }
59 //重新初始化桶,不然前后两次排序之间会有影响
60 //buckets[10][10000]={0};
61 //record[10]={0};
62 //InitialArray1(buckets,10,10000);
63 for (k=0;k<10;k++)
64 for (int m=0;m<100000;m++)
65 {
66 if(buckets[k][m]==0)break;
67 else buckets[k][m]=0;
68 }
69 InitialArray(record,10);
70 }
71 }
在这里需要注意的是由于局部变量桶过大可能会导致栈溢出而得不带结果,比如桶为int buckets[10][100000]={0};大小=(10*100000*4)/(1024*1024)=3.814M,如果栈的大小只有1M~3M的话就会溢出,就得不到结果,当然可以把这个局部变量改成全局变量。
下面是从数据量10~80000排序的实验结果,首先声明一点。每个排序算法的数据量是相同的而具体数据都是随机产生的,也就是每个排序一组不同的随机数据。这可能对实验结果有所影响。当然我这只是没事好奇搞着玩玩,结果仅供参考。大家有兴趣的可以自己试试!
数据量为10:

数据量为100:
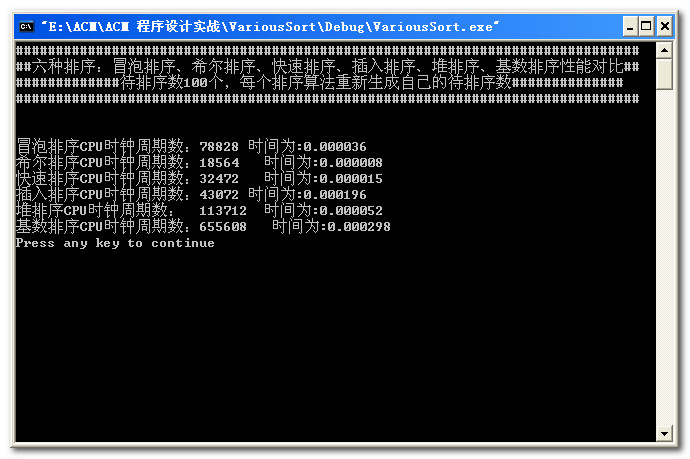
数据量为1000:
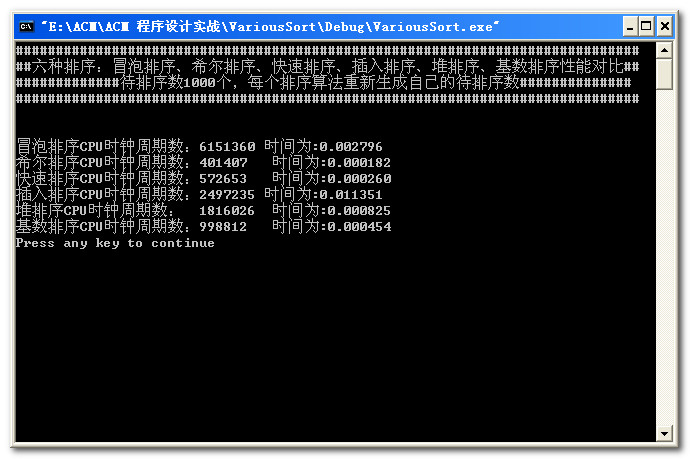
数据量为10000:
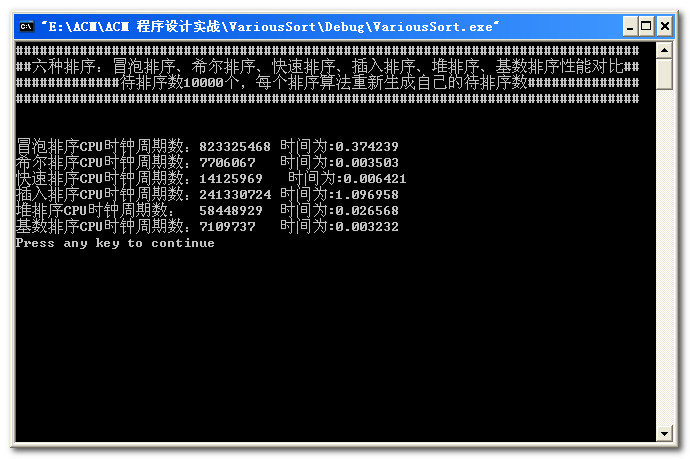
数据量为15000:
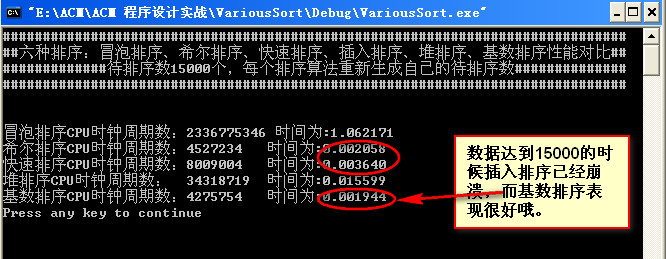
数据量为20000:
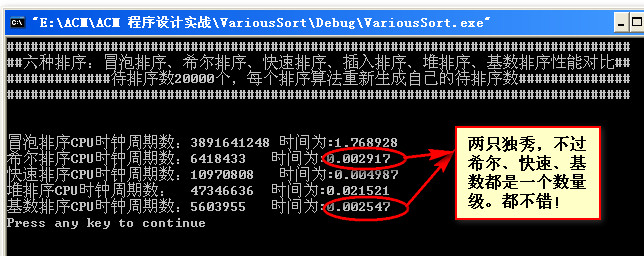
数据量为50000:
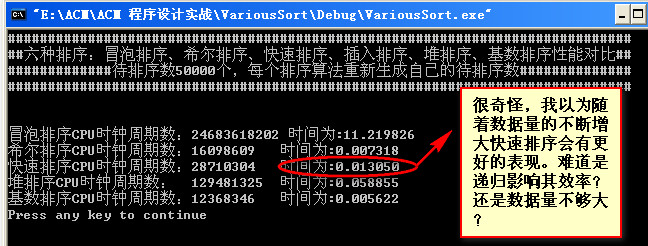
数据量为90000:

数据量为80000:
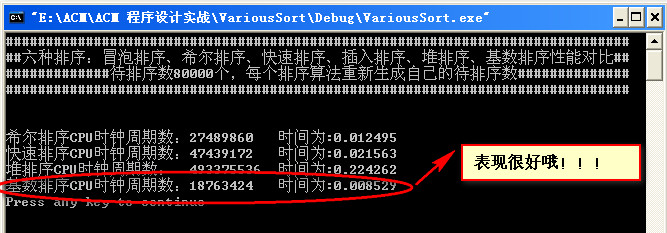
越来越兴奋了:


接下来想测一测10亿是神马情况程序直接挂了,然后测一测5亿然后就死机了,然后就木有然后了,我写了一半的博客!!!!!~~o(>_<)o ~~!!!!!~~o(>_<)o ~~!!!!!~~o(>_<)o ~~
后面测了一下5亿!本来录了一段小视频的,但是上传不了。这里就说出答案吧:5亿数据时,快速排序也挂了,只有希尔排序一直在健壮的运行,运行时间大概为120s左右。
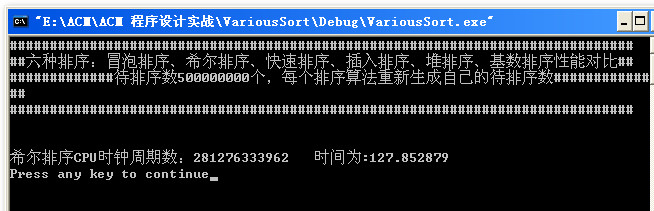
大概分析了一下数据所占的内存:
首先5亿个数据占多少内存?
(50000000*4)/(pow(1024,3))=1.86G
我的电脑内存为3G左右,除去操作系统和软件大约占了20%3G=0.6G。
3-0.6-1.86=0.54G剩余
0.54*pow(1024,3)/4=144955146剩余内存还可以计算1亿多个数据,
所以我的电脑一共能同时排序644955146个数据。这就是为什么排序10亿数据时程序崩溃的原因,因为没有这么多内存分配给程序使用。
然而我实际测了一下实际上达不到6亿,5.5亿就崩溃了,原因有待后续考察!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号