MATLAB时域分析

背景

MATLAB对时域分析有两个现成的函数： step(SYS)和impulse(SYS),分别对应阶跃响应和脉冲响应，实际上，响应还有斜坡和加速度响应等等，它们共同对应于系统的输入环节。输出往往使我们需要求解的。在两者之间的环节，可以用传递函数来描述，这里仅对一些分式形式的传递函数进行讨论，可以包括惯性环节、微分环节、积分环节、复合环节、二阶振荡环节等等进行分析。

这里的实例用了。

阶跃响应

。把分子分母的系数分别存入两个1维矩阵，然后直接调用step(num,den)，num是分子系数，den是分母系数。

num1 = [30 2];
den1 = [1 5 8 6];
step(num1, den1);
grid on;

效果：

单位脉冲响应

。把分子分母的系数分别存入两个1维矩阵，然后直接调用step(num,den)，num是分子系数，den是分母系数。

num1 = [30 2];
den1 = [1 5 8 6];
figure();
impulse(num1, den1);
grid on;

效果图：

斜坡响应

。把分子分母的系数分别存入两个1维矩阵，这里并没有现成的函数，但是我们知道单位阶跃和斜坡响应的拉氏变换值差一个s平方，所以不妨用单位阶跃除以一个s的平方来的到同样的结果。这里我利用了sys=tf()构造了两个系统，第一个是G，第二个是G1。tf转换效果就是构造一些系统，比如你输入两个一维矩阵，那么就会构造一个分式。s=tf('s')则是构造了一个拉普拉斯变量，这里是我们的复变量s，当然这个等号左边的字母只是增加了可读性，并不一定用s。所以说来，上面两个响应也可以用tf变换来实现，可参考附件资源。

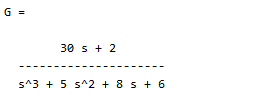
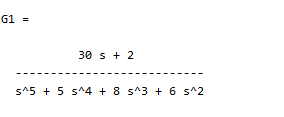
num1 = [30 2];
den1 = [1 5 8 6];
s = tf('s');
G = tf(num1, den1);
% divided by s^2 to transform impulse into ramp
G1 = G/s^2;
figure();
impulse(G1);
title('ramp response')
grid on;

效果图：