MATLAB频域分析,奈氏图、伯德图、对数幅相图绘制
绘图简介
在复平面上表示传递函数的幅值相位角随频率的改变而改变的图就是nyquist图(奈奎斯特图,奈氏图),表示控制系统的幅相频率特性,横坐标U(real number)纵坐标jV(imaginary number);伯德图(bode)利用对数表示系统的幅频、相频特性,它分为两个图,一个是对数幅频图、一个是相频图,横坐标均为w,纵坐标一个为,一个为
,
,
为相位角;而对数幅相图(nichols plot)则是将幅频和相频在一张图上表示出来了,横坐标是相位角fi(w)、纵坐标是增益K、然后图里面有不同的幅值线(幅值单位dB)。
这里的传递函数以惯性环节为例,也即,T取0.01。
奈氏图
分子分母的系数分别存入两个1维矩阵,这里我利用了sys=tf()构造了系统sys。tf转换效果就是构造一些系统,比如你输入两个一维矩阵,那么就可以构造一个分式。具体见这里。nyquist(sys)直接把一个传递函数输入,然后绘出奈氏图[re,im,w]=nyquist(sys)则是根据需要返回传递函数将s替换成jw后的实部、虚部,还有相应的频率。
num = [1];
den = [0.01 1];
sys = tf(num, den);
figure();
nyquist(sys);
[re, im, w] = nyquist(sys);
grid on效果图,图例看到不清楚,惯性环节的奈氏图是一个圆过(0,0)和(1,0):
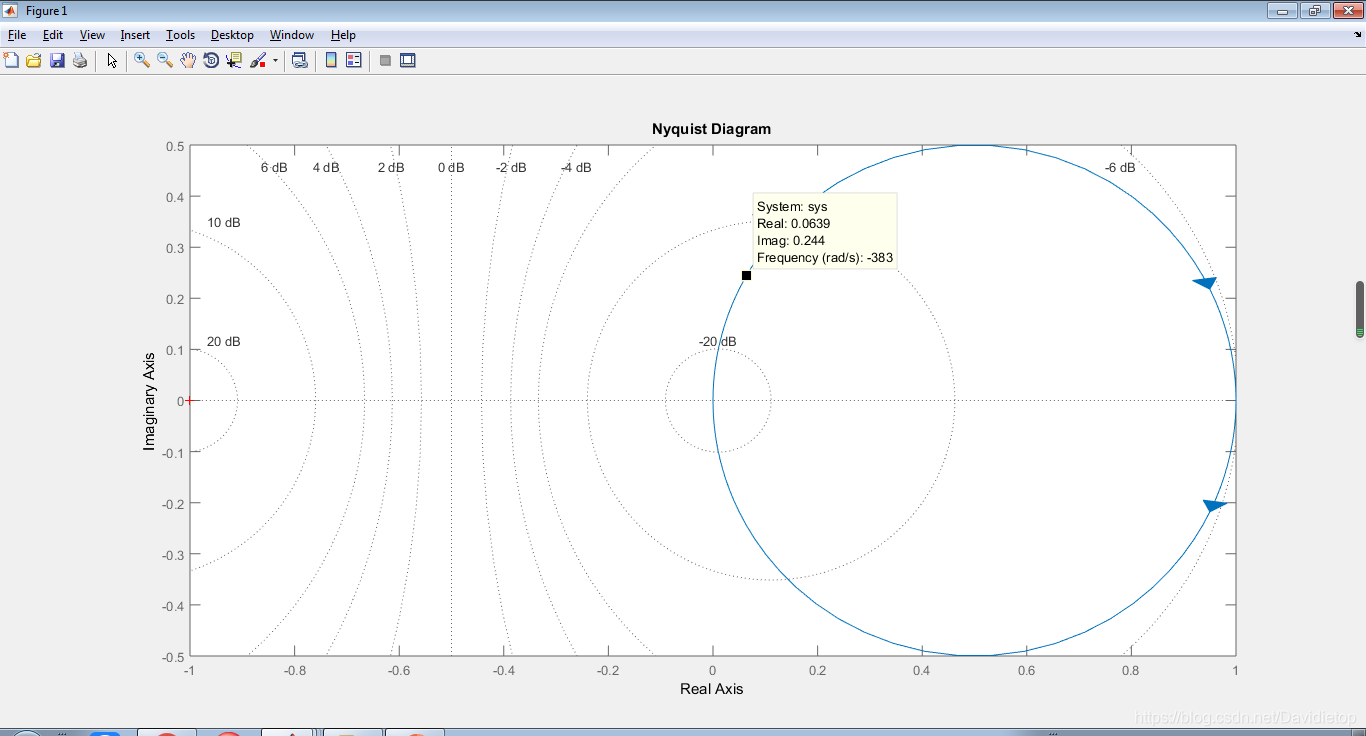
伯德图
和奈氏图的解释大同小异,函数是bode()。
num = [1];
den = [0.01 1];
sys = tf(num, den);
figure();
bode(sys);
[reb, imb, wb] = bode(sys);
grid on效果图:
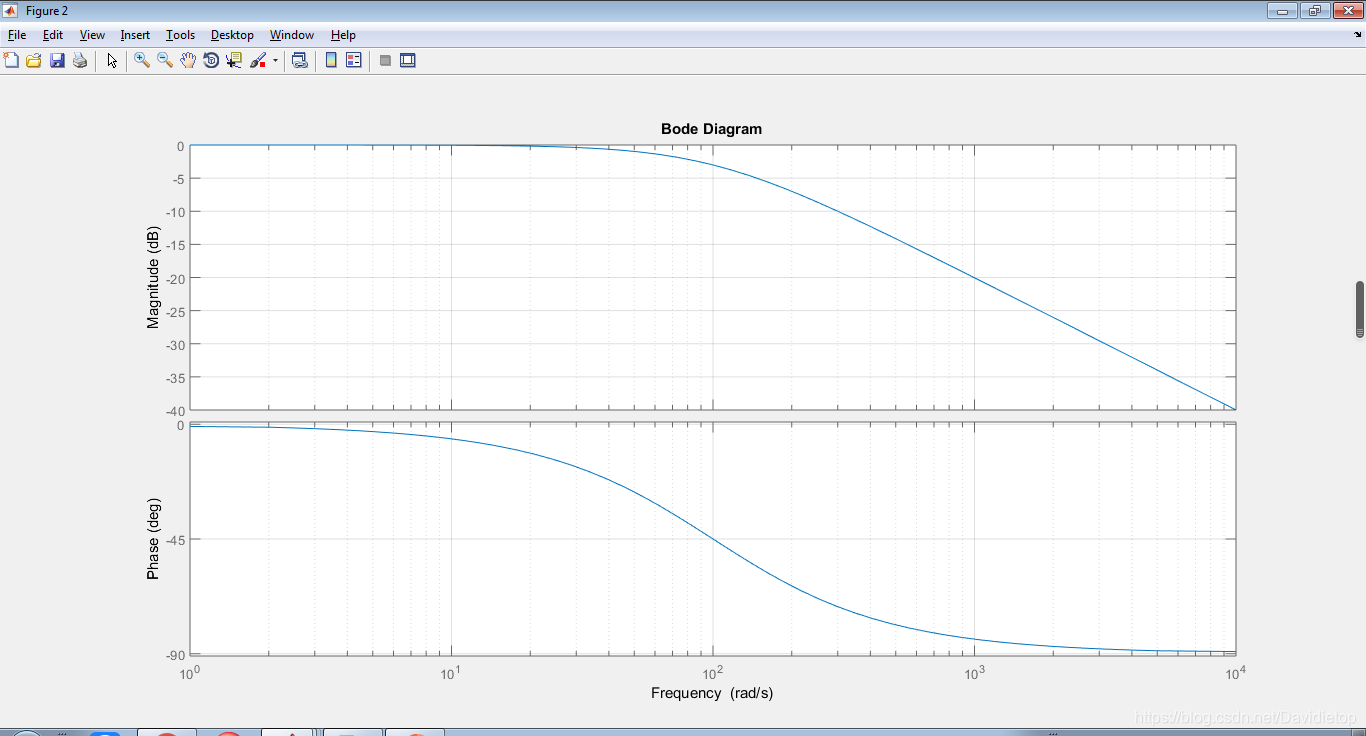
对数幅相图
解释同奈氏图,函数是nichols()。
num = [1];
den = [0.01 1];
sys = tf(num, den);
figure();
nichols(sys);
[reni, imni, wni] = nichols(sys);
grid on效果图:
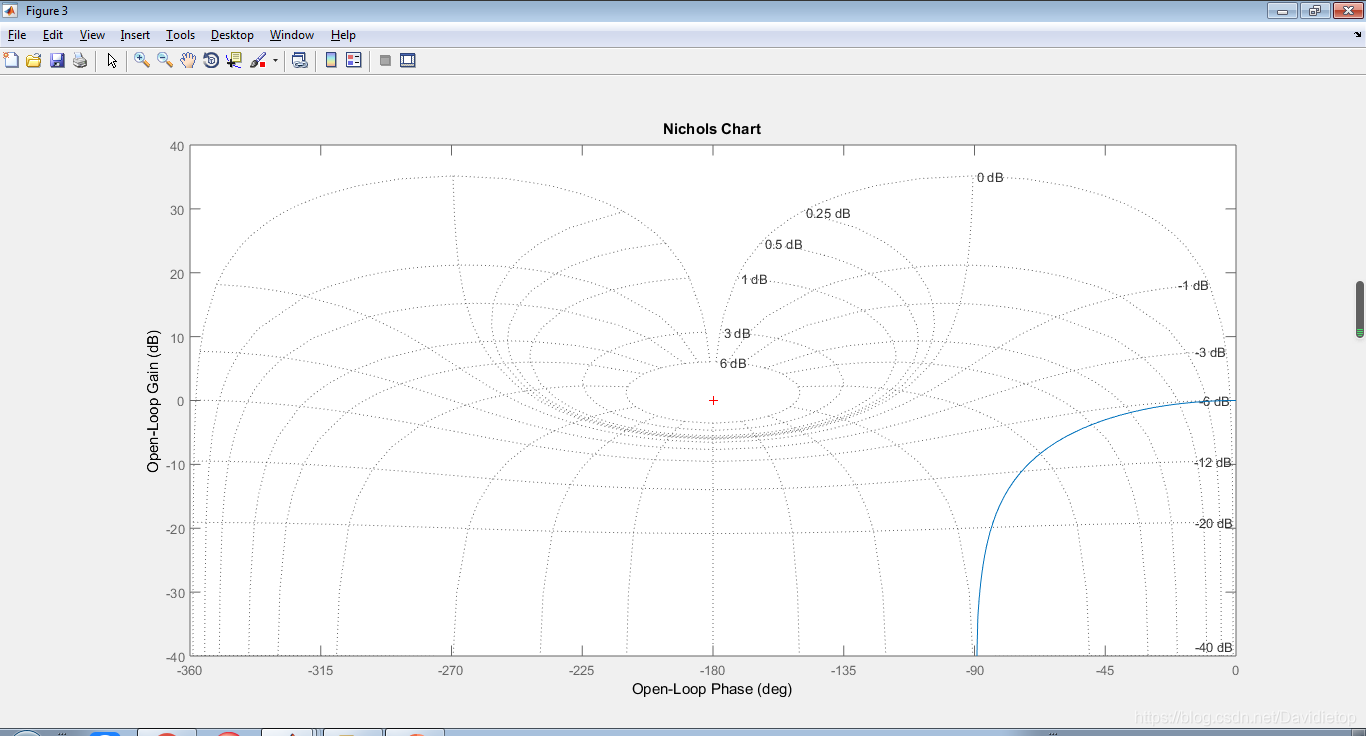




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)