信号处理趣学D1——相关函数的意义&利用自相关函数消除噪声
小虎在这里介绍了相关函数的意义和工程应用，工程应用以提取受噪声干扰的周期信号为例，并用MATLAB进行仿真。
什么是相关函数
相关函数(correlation function)是用来衡量两个信号的相关程度。相关函数又分为自相关函数、互相关函数和协方差函数。这里仅介绍在测试技术中较常见的两种（前两种）。
自相关函数
自相关函数(autocorrelation function)是用来衡量统一信号在不同时刻取值的相关程度。通过这种分析，可以分析出信号中的噪声并加以去除；或者从畸变的波形中分离出基波和谐波等。可以将时移前后的信号当成两个信号分析。这是仿真理解demo。
R
x
(
τ
)
=
lim
T
→
∞
1
T
∫
0
T
x
(
t
)
x
(
t
+
τ
)
d
t
R_x(\tau)=\lim \limits_{T \to \infty } \frac{1}{T} \int_0^Tx(t)x(t+\tau)dt
Rx(τ)=T→∞limT1∫0Tx(t)x(t+τ)dt
互相关函数
互相关函数(crosscorrelation function)用来衡量两个信号之间的相关程度和取值依赖程度。对于一个理想的测试系统的输入输出信号求相关函数，测试结果完美的情况下，互相关函数取最大值时的
τ
\tau
τ时为等于系统的滞后时间，因为这说明信号并没有损失或收到噪声干扰，给输入信号加上的延时
t
a
u
tau
tau后与输出的信号一模一样，所以相关程度为完全相同。这是仿真理解demo。
R
x
y
(
τ
)
=
lim
T
→
∞
1
T
∫
0
T
x
(
t
)
y
(
t
+
τ
)
d
t
R_{xy}(\tau)=\lim \limits_{T \to \infty } \frac{1}{T} \int_0^Tx(t)y(t+\tau)dt
Rxy(τ)=T→∞limT1∫0Tx(t)y(t+τ)dt
另有性质之一
R
x
y
(
−
τ
)
=
R
y
x
(
τ
)
R_{xy}(-\tau)=R_{yx}(\tau)
Rxy(−τ)=Ryx(τ)，所以当
y
(
t
)
y(t)
y(t)比较复杂时可以采用这种方法转换为对
x
(
t
)
x(t)
x(t)时延来计算。
相关函数提取周期信号原理
对机器进行噪声诊断时，噪声通常由随机、大量且大小近似相等影响因素叠加而成。随机噪声的自相关函数将出现规则的周期信号，幅值一般比正常噪声的幅值要大。当将变速箱各个机轴的转速化成频率与自相关函数波动频率比较，可以确定机械轴的好坏。或者利用自相关函数分析去除噪声得到周期函数的周期。
具体例子——MATLAB仿真示例
提取受到噪声干扰的周期函数 x = s i n ( w 0 t ) x=sin(w_0t) x=sin(w0t)的自相关函数,分析原周期函数的周期。
物理意义
结果如下图。为了便于计算，将
w
0
=
2
π
f
0
w_0=2\pi f_0
w0=2πf0计算。
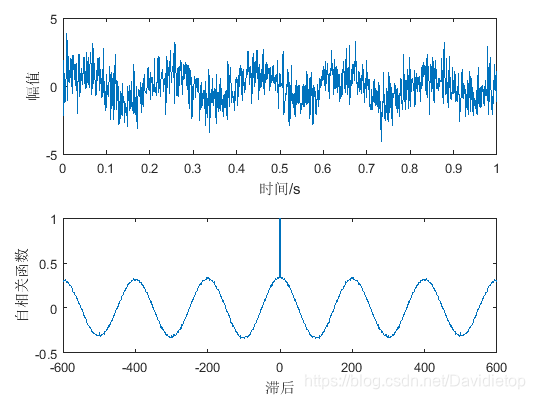
- 可以看到，每过一个周期，原周期函数重合，相关程度最高；每过半个周期，原周期函数互为相反数，相关程度为负的最大，这里我设的函数周期正好是0.2s（即200ms），可以很好的从自相关函数-滞后时间图像中看出。
- 横坐标0的时候，时移为零，函数图像重合，时移前后的两个函数完全相同，相关程度最大，所以出现了0时刻的正的尖峰。
- 另外，噪声的干扰还是可以在自相关函数-滞后时间的图中看出的，可以看到曲线不是完美的曲线，而是由波动的折线拟合而成的，这是随机噪声带来的影响，但是不影响我们分析周期函数的周期。
代码分析
- 参数设置
取6000采样长度，1000采样频率，t为采样间隔， w 0 = 2 π f 0 = 10 π w_0=2\pi f_0=10\pi w0=2πf0=10π。
n=6000;
fs=1000;
t=(0:n-1)/fs;
f0=5;
- 函数建立
x为周期为 1 / f 0 1/f_0 1/f0的正弦周期函数，z为x受到随机噪声干扰后的函数。
x=sin(2*pi*f0*t);
z=x+randn(size(x));
- 自相关函数求解
R是求得的自相关函数；tau时延的值，截取了包括0在内的1+600x2个点。600时时延的区间，以傅里叶复指数形式表示的频谱是双边谱，傅里叶三角函数表示形式是单边谱，这里为前者，其实是后者的一分为二，这完全是数学计算的结果，没有任何实际物理意义。'coeff’归一化求得是自相关函数，‘biased’是有偏估计，'unbiased’是无偏估计。
[R,tau]=xcorr(z,600,'coeff');
- 作图
用两个画板画出受噪声干扰的函数和改函数的自相关函数。
subplot(2,1,1);
plot(t(1:1000),z(1:1000));
xlabel('时间/s');
ylabel('幅值');
subplot(2,1,2);
plot(tau,R);
xlabel('滞后');
ylabel('自相关函数');
- 完整代码
n=6000;
fs=1000;
t=(0:n-1)/fs;
f0=5;
x=sin(2*pi*f0*t);
z=x+randn(size(x));
[R,tau]=xcorr(z,600,'coeff');
subplot(2,1,1);
plot(t(1:1000),z(1:1000));
xlabel('时间/s');
ylabel('幅值');
subplot(2,1,2);
plot(tau,R);
xlabel('滞后');
ylabel('自相关函数');
参考文献
[1]张春华等，工程测试技术基础第二版
