CF792D 完全二叉树上的路径
1 CF792D 完全二叉树上的路径
2 题目描述
时间限制 \(3s\) | 空间限制 \(256M\)
给出一棵节点数为 \(n\) 的完全二叉树,各节点标号从 \(1\) 到 \(n\)。其节点标号规则为中序标号:即标号时先标左子树,再标根节点,再标右子树。例如,一棵节点数为 \(15\) 的完全二叉树标完号后应如下图所示:
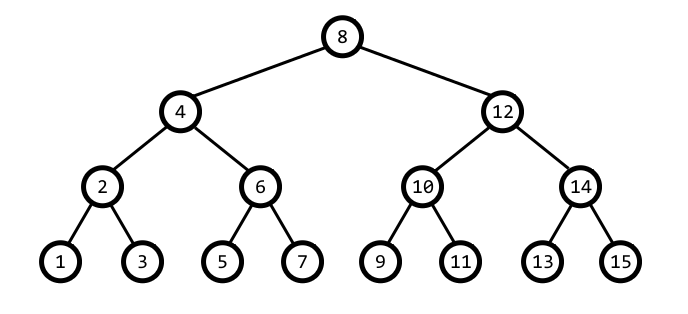
你要回答 \(q\) 次询问,每次询问由一个整数 \(u_i\) 和一个字符串 \(s_i\) 组成。询问的具体内容为:从编号为 \(u_i\) 的节点出发,经过字符串 \(s_i\) 所代表的移动后,最终到达的节点的编号是多少。
字符串 \(s_i\) 仅由 \(L, R, U\) 三种字符组成。其中,\(L\) 代表移动到当前节点的左儿子,\(R\) 代表移动到当前节点的右儿子,\(U\) 代表移动到当前节点的父节点。如果无法完成该移动(让叶子结点移动到左儿子或者让根节点移动到父节点),则跳过当前移动。
3 输入格式
第一行包括两个整数 \(n\) 和 \(q\)(\(1 \le n \le 10^{18}, q\ge 1\))。
接下来的 \(2*q\) 行代表 \(q\) 次询问。每连续的 \(2\) 行代表一次询问:第一行有一个整数 \(u_i\)(\(1 \le u_i \le n\)),第二行有一个字符串 \(s_i\)。
保证 \(\sum_{i = 1} ^ q \lvert s_i \rvert \le 10^5\)。
4 输出格式
共 \(q\) 行,每行一个整数,第 \(i\) 行的整数为第 \(i\) 次询问的答案。
5 样例输入输出:
| 样例1输入 | 样例1输出 |
|---|---|
| 15 2 4 UURL 8 LRLLLLLLLL |
10 5 |
6 题解
首先我们观察到 \(\sum_{i = 1}^{q}\limits |s_i| \le 10^5\),容易想到时间复杂度可能为 \(O(\sum_{i=1}^q\limits |s_i|)\)。这意味着, 我们必须找出一种办法,使得我们可以在 \(O(1)\) 的时间复杂度内求出任何节点的父节点、左儿子与右儿子。又由于 \(1 \le n \le 10^{18}\),我们无法暴力将整棵完全二叉树存储下来,只好寻找规律。
我们发现,整棵完全二叉树以 \(\frac {n+1}{2}\) 这一节点为中心,左右两侧子树的结构完全一致。而右侧子树中节点的编号减去 \(\frac {n+1}{2}\) 后即是左侧子树中相应位置的节点的编号。继续细分,可以发现:每个非叶子节点的节点的左子树和右子树都满足以上规律。因此,我们可以先讨论最左侧的那一条链的情况。我们很容易发现,在最左侧的链上,每个节点的编号是其父节点编号的 \(\frac {1}{2}\)。也就是说,当编号为 \(x\) 节点位于最左侧的链上时,其左儿子(如果拥有左儿子)为 \(x >> 1\),其父节点为 \(x << 1\)。这时,我们向右侧开始推进。容易发现,对于左侧的链上的节点,其右儿子(如果拥有右儿子)为 \(x >> 1 + x\)。
由于右子树的节点编号全部为根节点编号加上左子树编号,且根节点的编号一定为 \(2\) 的整数次幂,右子树与左子树的唯一区别就是最高位多了一个 \(1\)。为了排除这个 \(1\) 对答案的影响,我们重新寻找规律,发现:由于我们在 \(x >> 1\) 中实际上只移动了一位二进制位(\(x\) 为 \(2\) 的整数次幂),并且所有的与这一位相关的右子树中的节点一定是在其二进制高位增加 \(1\) 的个数,这一操作推广到所有节点就是将该节点的最低位的 \(1\) 移动到更低一位。换言之,对于节点编号为 \(x\) 的节点,其左儿子(如果拥有左儿子)的节点编号为 \((x \bigoplus lowbit(x)) \bigoplus \frac{lowbit(x)}{2}\)。右儿子与类似,表示出来就是将一个节点编号的最低位再低一位的那一二进制位变为 \(1\)。换言之,对于节点编号为 \(x\) 的节点,其右儿子(如果拥有右儿子)的节点编号为 \(x \bigoplus \frac{lowbit(x)}{2}\)。接下来,我们可以根据跳转到左右儿子的规律反推出左儿子的父节点编号和右儿子的父节点编号。
我们通过上面的规律,发现:如果一个节点是左儿子,那么它的最低的为 \(1\) 的二进制位的上面一位一定为 \(0\);如果一个节点是右儿子,那么它的最低的为 \(1\) 的二进制位的上面一位一定为 \(1\)。这是因为一个节点的左儿子一定是先把其父节点的最低位清 \(0\),再往更低位添加一个 \(1\) 得到的。而右儿子是直接将最低的为 \(1\) 的那一位的更低位变为 \(1\),中间没有空隙。通过这个结论,我们可以轻易地确认一个节点是左儿子还是右儿子:将这个节点编号 \(x\) 与 \(lowbit(x) * 2\) 异或,如果得出的答案小于 \(x\),说明是右儿子,否则是左儿子。
我们确定了左儿子还是右儿子后,就可以计算出其父节点了:如果节点编号为 \(x\) 的节点是左儿子,父节点(如果拥有父节点)的节点编号就是 \((x \bigoplus lowbit(x)) \bigoplus (lowbit(x) * 2)\),如果节点编号为 \(x\) 的节点是右儿子,父节点(如果拥有父节点)的节点编号就是 \(x \bigoplus lowbit(x)\)。
最后我们再来看看什么情况下我们无法跳跃到儿子节点或者父节点:我们发现,所有的叶子结点的编号都是奇数,这是因为如果一个节点的编号是奇数,那么该编号的最低位为 \(1\),这时我们无法往更低位塞数了,我们就无法找到其儿子节点。而当一个节点的编号是 \(2^{n+1} - 1\)时,它就是最上面的那个根节点,它就没有父节点。
7 代码(空格警告):
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
#define int long long
int n, q, u, Lowb;
string s;
int lowbit(int x)
{
return x & (-x);
}
signed main()
{
cin >> n >> q;
for (int i = 1; i <= q; i++)
{
cin >> u >> s;
for (int j = 0; j < s.length(); j++)
{
Lowb = lowbit(u);
if (s[j] == 'L')
{
if (u & 1) continue;
u ^= Lowb;
u ^= (Lowb >> 1ll);
}
else if (s[j] == 'R') {if (!(u & 1)) u ^= (Lowb >> 1ll);}
else
{
if ((Lowb << 1ll) == n+1) continue;
if ((u ^ (Lowb << 1ll)) < u) u ^= Lowb;
else
{
u ^= Lowb;
u ^= (Lowb << 1ll);
}
}
}
cout << u << endl;
}
return 0;
}
欢迎关注我的公众号:智子笔记



 浙公网安备 33010602011771号
浙公网安备 33010602011771号