数据分析的层级
心理学研究有四个目的——描述、解释、预测、控制——本文借以表述数据分析的4个层级。
描述
第一个层级是描述——可以理解为用数据来描述某个事物。
用数据来描述某个事物的第一步是量化——通过数值来描述或者衡量某个事物的某种属性或状态——最终得到的数值可以是通过某个公式计算到的,也可以是多个“专家”进行主观评定的。
得到单个数值并不能说明什么问题,要想让数值产生价值,最简单的操作就是对比——通过和某个参照值进行对比进而判断表现的好坏。
为什么需要对比?
假设小明考试考了90分(满分100分),首先90分表示小明正确回答了90%的问题,不过90分到底好不好,需要比较后才能知道:
- 可以和同班同学比,这次考试,全班平均分是92分,看来小明的成绩没有达到中等水平;
- 也可以和小明的历史成绩比,上一次小明的考试是60分呢,哇塞,长进很大哦。
我们可以把关注的指标和参照值对比发现的gap值称为Δ值——可以将delta值理解为差异值或者变化值,更多可以可以参考前文《从“Δ值”谈数据分析》.
在“描述”这个层级,对应的数据分析的典型工作是报表开发。
- 列举关键指标数值及发展趋势,展示业务达标情况,e.g.KPI的完成情况,和KPI的差距;
- 拆解业务关键指标,可以参考加权公式进行横向维度上的拆解或者纵向业务环节的拆分;
- 设定各自指标的基准参照值,以揭示指标的波动情况(delta值)。
关于“描述”部分,小结如下
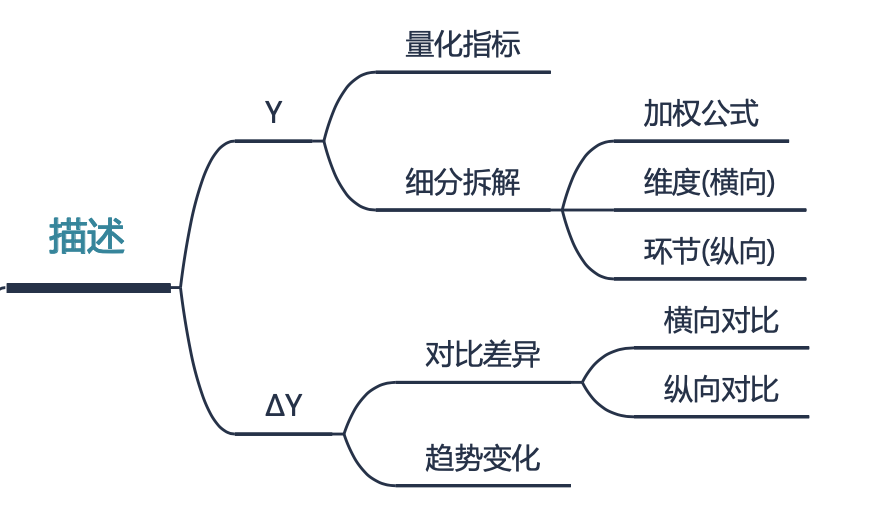
解释
\(\Delta X \leftarrow \Delta Y\)
数据分析中经常需要应对的问题是指标的波动——如果将波动的指标命名为Y,那么此时就需要找出是哪些因素引发了\(\Delta Y\).
e.g. 某一天观察到app的日活下降了很多(同比于上一周期),作为分析师你应该怎么做?
指标的波动时相对于历史数据而言(纵向对比),另一个典型的\(\Delta Y\)出现的场景是组间差异(横向对比),比如在某些业务场景下,你可能发现两个不同的用户群在某指标上表现的差异很大,那么你可能想知道导致这种差异的原因。
除此之外,以下场景也是和ΔY有关的高频场景
- 为什么某个细类拖了整体的后腿?
- 为什么业务表现低于预期KPI?
- 为什么业务低于竞争对手?
我们用公式 \(\Delta X \leftarrow \Delta Y\) 来表示针对变化量的归因。
对于变化量的归因,一般流程如下:
- 判断波动的严重程度,需要设置对比的参照值和波动报警的阈值;
- 排除数据问题,比如底层表是不是有改动或者有人修改了报表中的指标规则,一般来说新上线的业务比较容易出现数据问题;
- 定位问题环节,将\(\Delta Y\)在更细的维度上拆解,时间维度上可以看是什么时候开始的以及持续了多久,空间维度上可以从“人货场”各维度拆分,看看是什么用户群、商品、业务场景问题最严重;
- 是否历史有类似情况或者波动规律;
- 先查内因(渠道入口、转化环节、人货场);
- 再查外因(政策、市场、竞品等);
这个顺序也不是绝对的,总体来说的原则有两点:
- 定位变化发生的环节;
- 按概率从高到低来排查可能的影响因素;
\(X \leftarrow Y\)
除了关注变化量ΔY外,我们还关注有哪些影响因素会影响业务上的关键指标。
这里用 \(X \leftarrow Y\) 来表示,注意箭头的方向。
\(X \leftarrow Y\) 和 \(\Delta X \leftarrow \Delta Y\) 有一部分内容是重叠的,一般来说,对\(\Delta Y\) 有影响的因素也是对\(Y\)有影响的。
不过\(X \leftarrow Y\) 更强调找到影响关键指标\(Y\)的影响因素X,并建立相应的函数 \(Y = f(X)\).
这些\(X\)中就包含了在产品或运营上可操作可控制的因素。
e.g. 访问用户数 * 下单率 * 客单价 = 销售额,基于这个简单的公式可以判断,如果要提升销售额至少可以从三个角度来着手。
关于“解释”,小结如下
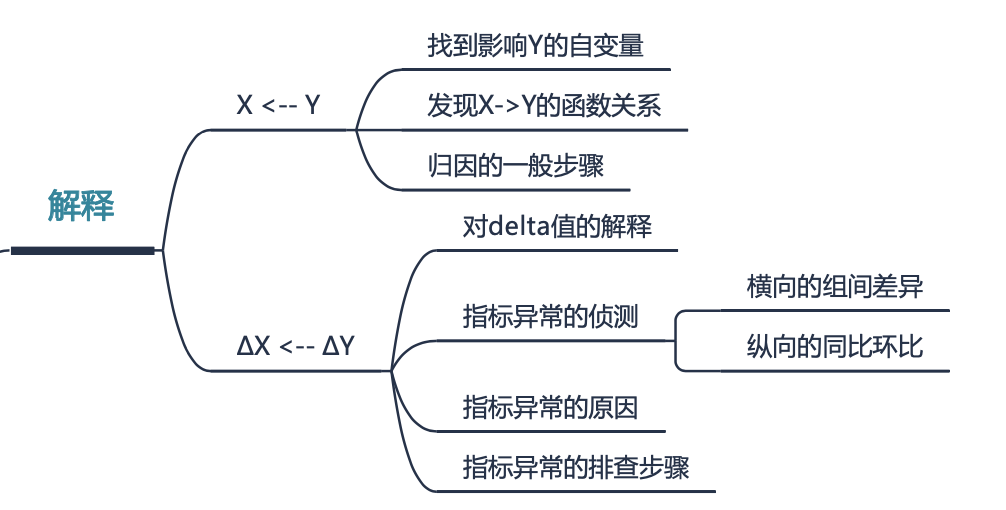
预测
这部分的内容,在文章《预测的方法》中已有较详尽的说明,请阅读此文。

如上图所示,预测有3个角度。
\(X \rightarrow Y\)
对应“解释”中\(X \leftarrow Y\) 的逆操作——从已知的X来推导未知的Y。
这个过程可以看做是evaluate,可以使用如下两种方法:
- 基于关联原则来类推,简称“类推法”,也就是先归类,然后推导。比如格子衫、发量少、戴眼镜、男性、程序员这几个特征是高度关联的,知道“格子衫”和“发量少”就能推断出此人职业很可能是“程序员”;
- 基于目标数据和已知数据存在“函数关系”,简称“函数法”或者“公式法”,即\(Y=f(X)\),基于函数规则就能计算得到目标数据\(Y\)。比如评估某次产品运营活动对交易产生的影响量(Y),那么对应需要考虑的X可能包含活动覆盖的人群属性、人群数量、活动方式、优惠力度等;
\(\Delta X \rightarrow \Delta Y\)
相当于what if分析。
比如某个产品功能要改动,需要预估这个改动可能带来的影响,比如影响的范围(多少用户,多少订单等),以及对业务关键指标可能产生的波动范围。
\(Y_{t_1},Y_{t_2},..., Y_{t_k} \rightarrow Y_{t'}\)
基于“时间序列”来预估未来的数据,相当于forecast,比如股票走势、业务发展趋势、交易量预估等。
控制
从心理学研究的角度来看,能控制改变人的认知和行为是最高层级——这样看来,X教授的能力应该算是最强的了。
不过,从数据分析的角度来说就没有那么“科幻”了。
可以从两个角度来看数据分析在“控制”这个层级的工作:
- 收益角度
- 函数角度
收益角度
降本增效是商业的核心追求,数据则是要辅助这个目标的实现。
可以从3方面着手:
- 提升收入(做加法),比如提升每单位交易收入(客单价、ARPPU等)或者提升交易基数(用户量、订单数等);
- 降低成本(做减法),减少人力、物力、资金的投入;
- 提升效率(做乘法),提高单位时间的完成量或者周转率等;
函数角度
- 超越预设目标
\(G(cost, limit, way) \geq target\) - 最大化目标函数
\(Max\bigl( G(cost, limit, way) \bigr)\)
注:
cost可以投入的资源或成本,比如人力、物力、金钱、时间等;limit受到的限制,比如外部PEST的限制,或者行业的瓶颈等;way可以到达目标的可选路径;target预设的目标或期望的收益;- \(G(cost, limit, way)\) 相当于收益的目标函数
本小节小结如下

本博客所有文章仅用于学习、研究和交流目的,欢迎非商业性质转载。
转载请注明作者及出处


 浙公网安备 33010602011771号
浙公网安备 33010602011771号