机器学习基础 | 偏差与方差
偏差和方差的分解
在有监督学习中,通过训练数据得到的模型,需要考察其泛化能力,通常用泛化误差来衡量模型泛化能力的高低。
也可以用测试误差来衡量模型泛化能力,不过测试的样本是有限的(而且难以保证不是有偏的)。基于大数定律,假设每次参与模型训练的样本都是独立同分布的(实际有点难,会有样本重叠),那么从多个训练样本中得到的经验误差(训练样本集上的平均损失)的期望就等于泛化误差,也就是说,多个样本上的平均训练误差是接近泛化误差的。
泛化误差可以分解为3部分,即泛化误差=偏差+方差+噪声。
这里以回归任务为例来说明泛化误差的分解。回归任务中常使用平方损失函数(quadratic loss function)来衡量模型预测的错误程度,该损失函数的基本形式为(统计学习方法,李航):
其中\(Y\)为真实值,\(f(X)\)为模型预测值。
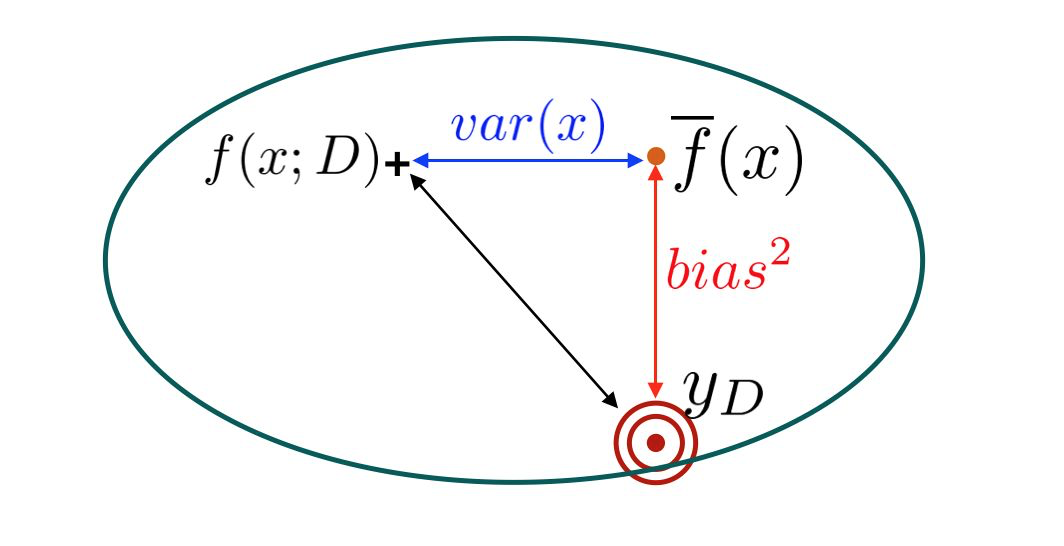
设\(x\)为测试样本,\(y_D\)为样本在数据集中的标记,\(y\)为样本的真实标记,\(f(x;D)\)为训练集\(D\)上学到的模型\(f\)在\(x\)上的预测输出,其期望值为
那么:
- 偏差为模型预测值的期望值与真实值之间的差距
- 方差为使用不同样本得到的预测值的变异性
- 噪声则是样本在数据集中的标记与真实标记之间的偏离
- 对应的期望泛化误差为
泛化误差可以分解为偏差、方差和噪声,推导过程如下(参考《机器学习》,周志华)
上面公式中的灰色部分为0(假设噪声的期望\(\mathbb{E}_D[y_D-y]=0\)),这样我们就得到了如下公式,完成了回归任务下的泛化误差分解。
泛化误差的分解有什么意义呢?
- 首先噪声是模型学习的上限(也可以说是误差的下限) ,不可控的错误很难避免,这被称为不可约偏差(irreducible error),即噪声无法通过模型来消除。噪声通常是出现在“数据采集”的过程中的,且具有随机性和不可控性,比如数据标注(通常会有人工参与)的时候手滑或者打了个盹、采集用户数据的时候仪器产生的随机性偏差、或者被试在实验中受到其他不可控因素的干扰等;
- 其次是方差,方差反映了在不同样本集上模型输出值的变异性,方差的大小反应了样本在总体数据中的代表性,或者说不同样本下模型预测的稳定性。比如现在要通过一些用户属性去预测其消费能力,结果有两个样本,一个样本中大多数都是高等级活跃会员,另一个则是大部分是低质量用户,两个样本预测出来的数据的差异就非常大,也就是模型在两个样本上的方差很大。如果模型在多个样本下的训练误差(经验损失)“抖动”比较厉害,则有可能是样本有问题;
- 最后是偏差,偏差体现了模型对训练数据的拟合能力。把模型比喻成一支猎枪,预测的目标是靶心,假设射手不会手抖且视力正常,那么这支枪(模型)的能力就可以用多次射击后的中心(相当于预测值的期望,即\(\overline{f}(x)\))和靶心的距离来衡量(偏离了靶心有多远)。当猎枪(模型)和子弹(样本)质量都很好时,就能得到方差和偏差都比较低的结果。但是猎枪可能是没有校准的或者目标超出有效射程,那么偏差就会更高(击中点离靶心比较远)。子弹(样本)也可能出问题,比如子弹的形状、重量等因素,导致瞄准一个点多次射击在靶上会散开一片,这就是高方差的情况。
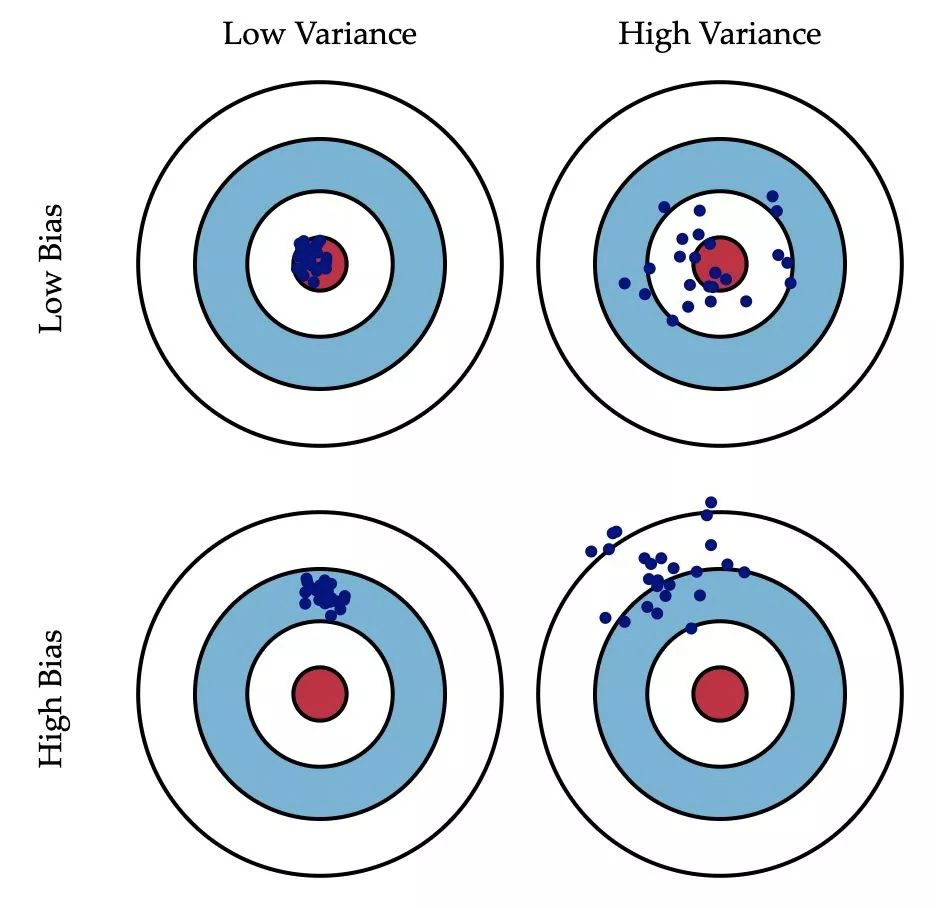
也可以用下图来表示方差和偏差的关系:
偏差和方差的权衡
关于偏差和方差的权衡(bias-variance tradeoff)
偏差和方差的权衡是指,随着模型复杂度(Model Complexity)变化,方差和偏差会此消彼长的现象(如下图所示)。
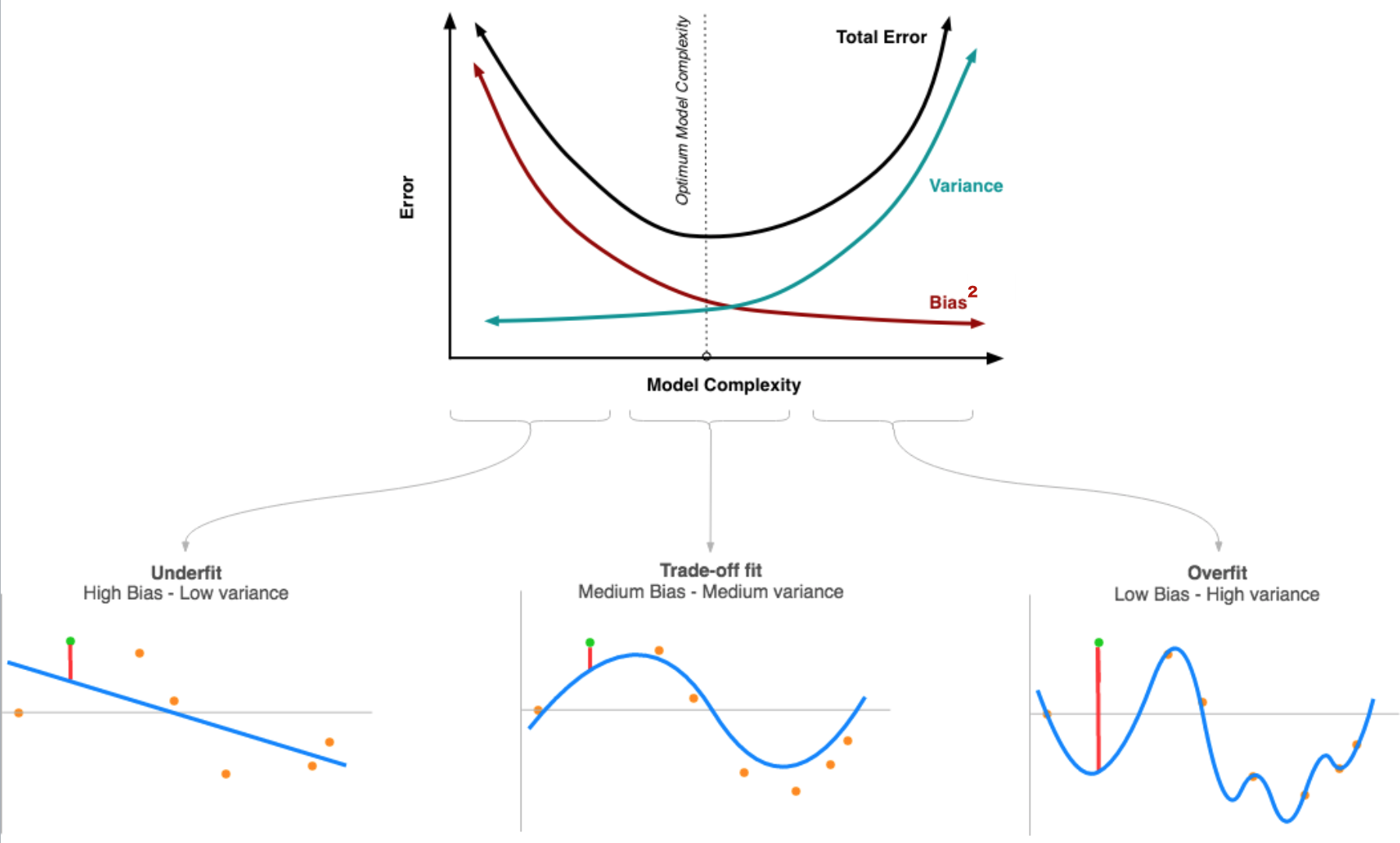
模型训练不足时,就出现欠拟合(under-fitting),此时模型的误差主要来自偏差,如果是在分类任务中可能在训练集和测试集上的准确率都非常低(反过来说就是错误率都很高);
训练模型时用力过猛时就会发生“过拟合” (over-fitting),在分类任务上可能会出现训练集上准确率高,测试集上准确率低。此时样本本身的特异性也会纳入模型之中,导致预测值的变异性更大。
如何降低偏差(bias)?
参考Machine Learning Yearning,Andrew Ng
- 增加算法的复杂度,比如神经网络中的神经元个数或者层数,增加决策树中的分支和层数等。不过增加模型复杂度可能会导致方差(variance)的增加,如果有必要,需要添加正则化项来惩罚模型的复杂度(降低方差);
- 优化输入的特征,检查特征工程中是否遗漏掉具有预测意义的特征。增加更多的特征也许能同时改善方差(variance)和偏差(bias),不过理论上来说,特征越多方差(variance)也就越大(可能又需要正则化);
- 削弱或者去除已有的正则化约束(L1正则化,L2正则化,dropout等),不过有增加方差的风险;
- 调整模型结构,比如神经网络的结构;
如何降低方差(variance)?
参考Machine Learning Yearning,Andrew Ng
- 扩大训练样本,样本太小(代表性不够)是方差大的首要原因,增加样本是减少方差最简单有效的方式;
- 增加正则化约束(比如L1正则化,L2正则化,dropout等),正则化降低方差的同时也可能增大偏差;
- 筛选输入的特征(feature selection),这样输入的特征变少后,方差也会减小;- 降低算法模型复杂度,比如对决策树的剪枝、减少神经网络的层数等;
- 优化模型的结构有时候也会有用;
K最近邻算法(K-NearestNeighbor)中随着K的增大bias和variance会怎么变化?
从计算的角度看,随着K(邻居数)增大模型好像更加复杂了(需要迭代更多的数据点,消耗更多的计算资源)。但是从模型角度考虑“复杂程度”(complexity)的时候应该看预测结果的变异性(variability),而不是计算过程的“复杂程度”,结果的变异性越大(复杂度越高)那么方差就越大。如下图所示,K=0时KNN的决策边界更显得“崎岖不平”,这说明决策的过程更加复杂,对应的方差也更大,反之K=100时的决策边界很平滑,此时的方差更小;
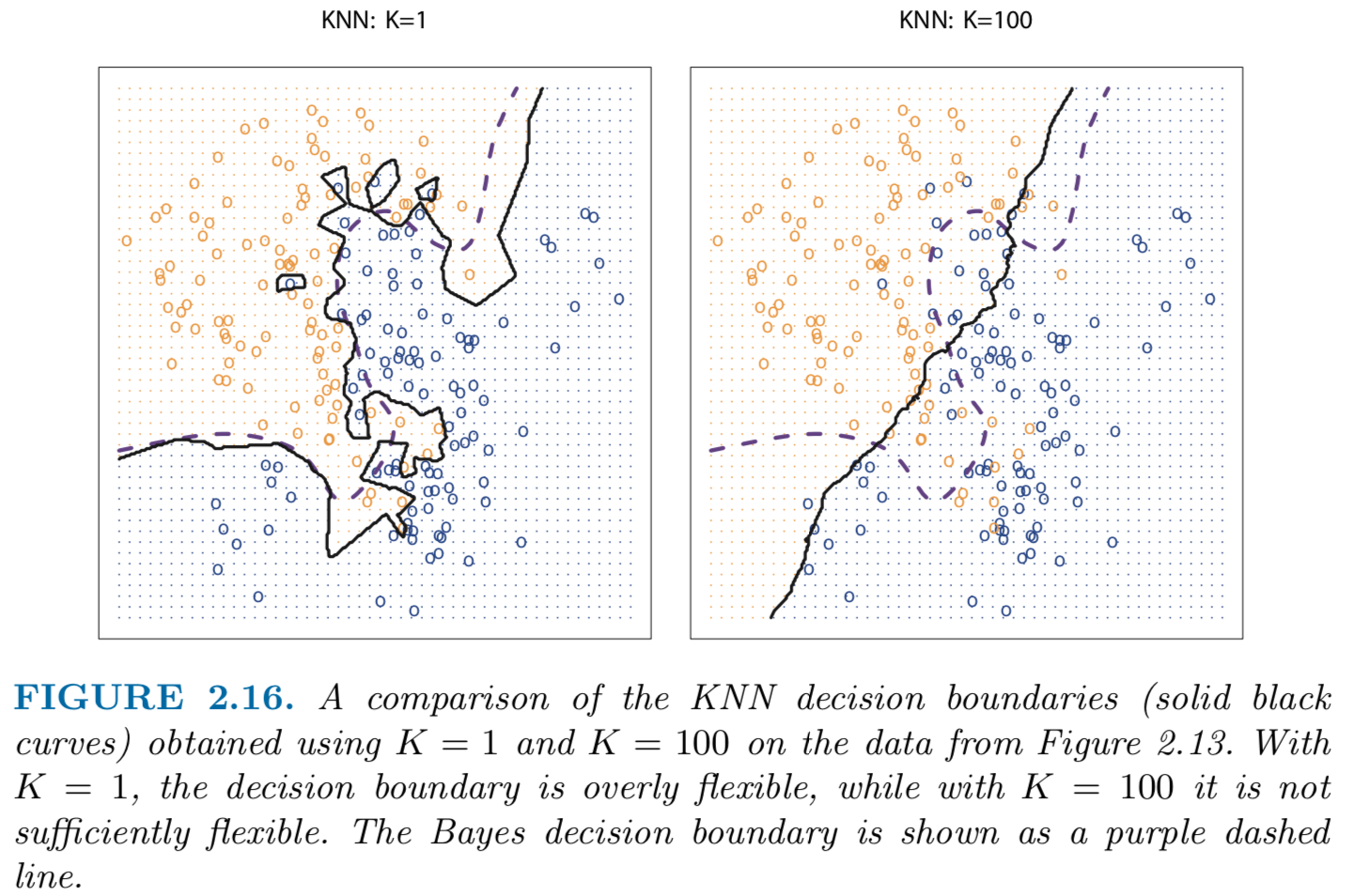
截图来自:An Introdunction to Statistical Learning, with Applications in R
对KNN模型对应的泛化误差进行偏差-方差分解(bias-variance decomposition),可得到如下表达式(见参考资料3):
可以发现方差和K是成反比的。
通常来说:
- 线性或者参数化的算法一般具有高偏差(bias)低方差(variance)的特点,比如线性回归,线性判别分析(Linear Discriminant Analysis),Logistic回归等线性模型;
- 非线性或者非参数化的算法则常表现出低偏差(bias)高方差(variance),比如决策树,KNN,SVM;
参考资料
- 机器学习,周志华;
- 统计学习方法,李航;
- http://scott.fortmann-roe.com/docs/BiasVariance.htm
- Machine Learning Yearning,Andrew Ng
- https://machinelearningmastery.com/gentle-introduction-to-the-bias-variance-trade-off-in-machine-learning/
本博客所有文章仅用于学习、研究和交流目的,欢迎非商业性质转载。
转载请注明作者及出处


 浙公网安备 33010602011771号
浙公网安备 33010602011771号