pytorch入门2.1构建回归模型初体验（模型构建）

pytorch入门2.x构建回归模型系列:
pytorch入门2.0构建回归模型初体验（数据生成）
pytorch入门2.1构建回归模型初体验（模型构建）
pytorch入门2.2构建回归模型初体验（开始训练）
终于要构建模型啦。这里我们构建的是回归模型，是用神经网络构建的，基本结构是什么样的呢？
你肯定听说过，神经网络有输入层、隐藏层、输出层，一般结构如下图所示（图片来源于网络，侵删）：

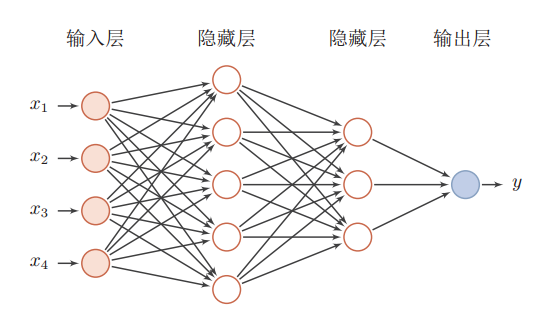
所以，对比我们之前生成的数据来说，形如x=3我们想得到的输出为y=8。分别对应了上面的输入层和输出层，所以，在此我们要构建中间的隐藏层来模拟那个看不见的函数（我们生成数据的函数，假设是未知的，因为如果是已知的，我们直接用这个函数式子来求输出啦。现在就是利用神经网络强大的对函数的拟合能力，来模拟这个函数）。
下面就来建立第一个模型吧：

class LinearRegression(nn.Module):  # 继承父类nn.Module，很多额外的、重要的东西就不用写了，只管自己做的事情就可以（你不是要建立回归模型么）
    def __init__(self):
        super(LinearRegression,self).__init__()  # 调用父类的初始化函数
        # 建立隐藏层，下面是三个隐藏层
        self.linear = nn.Linear(1,10)  # 输入是一个数，所以输出是1，中间建立10个隐藏层节点，此时，你输出的是10个数 
        self.linear2 = nn.Linear(10,6,bias=True)  # 承接上一层的输入，10个数，此层在融合成6个数。这里加了个偏置参数。 
        self.linear3 = nn.Linear(6,1)  # 输出层，承接上面6个数，最终输出一个数
        # 至此网络的部件定义完毕

    # 网络的部件定义好了，下面开始组装啦，设置数据如何在网络中流动，即前向传播
    def forward(self,x):  #输入的是x，就是指前面的输入层的输入
        # 设置数据流动过程，如果网络非常复杂，此处要注意输入数据的维度，经过各层之后得到的数据维度。
        x = F.relu(self.linear(x))  #首先经过一个线性层linear，然后经过一个激活函数relu
        x = F.relu(self.linear2(x))  #同上
        x = self.linear3(x)  # 最终经过最后的线性层，得到结果，结果是1维的哦
        return x  # 返回最后得到的数据

经过上面之后，一个网络模型就定义完成了，动动脑筋想想我们构建的模型是怎么样的呢？就是形如上面那张图的样子，只是中间的节点数量会变化。
模型定义好了，当然我们用的时候要实例化，我们先实例化一下，打印出来看看模型啥样？

model = LinearRegression()
print(model)
'''
===output===
LinearRegression(
  (linear): Linear(in_features=1, out_features=10, bias=True)
  (linear2): Linear(in_features=10, out_features=6, bias=True)
  (linear3): Linear(in_features=6, out_features=1, bias=True)
)
'''

可以看到模型的形状正如我们上面所介绍，网络模型是有三个线性层，这里把激活函数省略了。
下一节，我们继续介绍如何使用定义好的网络模型去做回归训练啦。