力扣-盛水最多的容器

盛水最多的容器

题目：

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

来源：力扣（LeetCode）

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

case:

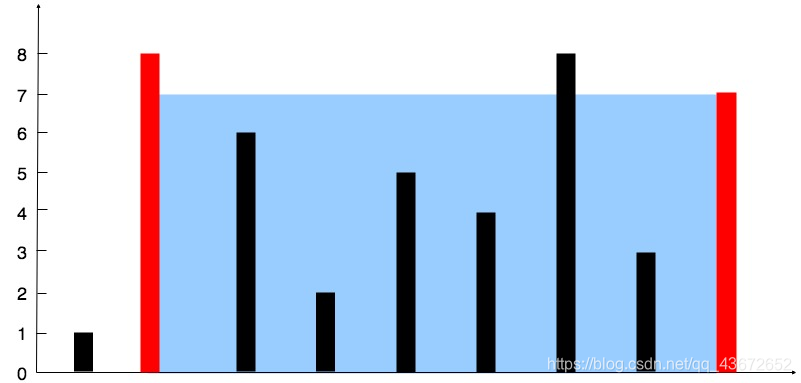
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
示例 2：
输入：height = [1,1]
输出：1
示例 3：
输入：height = [4,3,2,1,4]
输出：16
示例 4：
输入：height = [1,2,1]
输出：2

思路

设i容器数组的左边界，j是右边界，区间[i,j]，j-i 表示容器的宽；高度取height[i],height[j]两者较小的，然后面积S=max(S,(j-i)*min(height[i],height[j]));
这时，需要保证在容器宽度一致的情况下，选出较高的短板，主要是移动两边的短板的策略是什么？

因为不管左指针向内侧移动还是右指针向内侧移动，容器的宽度都会-1，因此为了让容器在宽度变化一致的情况下，面积最大，让两侧短板中高度较低的向内侧移动。

为什么呢？因为如果让两测较高的向内侧移动，说明固定较小的短板，向内侧移动，宽度变小，然而水位高度最大也只是和短板高度相等，所以面积减小；如果让较低的短板向内侧移动，说明固定高的短板，说明水位高度有可能等于较高短板的高度，因此有比之前面积增大的机会。

这道题的思想就是使用双指针，缩减搜索空间，减少容器面积无关状态。

代码

class Solution {
    public int maxArea(int[] height) {
        int res=0,i=0,j=height.length-1;
        while(i<j){
            //容器最大面积：在容器宽度一致的情况下，让容器高度尽量高,容器高度取两侧较低的值
            res = Math.max(res,(j-i)*Math.min(height[i],height[j]));
            if(height[i]>height[j]){
                //高度较小的向内侧移动
                j--;
            }else{
                i++;
            }
        }
        return res;
    }
}