0-1背包实验
实验名称
动态规划（0/1背包）
实验目的
1.掌握动态规划的基本思想；
2.学习写动态规划递推方程；
3.编写动态规划算法。
实验内容
采用动态规划法求解0-1背包问题。
实验环境
操作系统：Win10；
编程语言：Java；
开发工具：IDEA；
问题描述
有n 个物品，它们有各自的重量和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值总和？
总体思路
根据动态规划解题步骤（问题抽象化、建立模型、寻找约束条件、判断是否满足最优性原理、找大问题与小问题的递推关系式、填表、寻找解组成）找出01背包问题的最优解以及解组成，然后编写代码实现。
动态规划
动态规划与分治法类似，都是把大问题拆分成小问题，通过寻找大问题与小问题的递推关系，解决一个个小问题，最终达到解决原问题的效果。但不同的是，分治法在子问题和子子问题等上被重复计算了很多次，而动态规划则具有记忆性，通过填写表把所有已经解决的子问题答案纪录下来，在新问题里需要用到的子问题可以直接提取，避免了重复计算，从而节约了时间，所以在问题满足最优性原理之后，用动态规划解决问题的核心就在于填表，表填写完毕，最优解也就找到。
实验过程
- 将背包问题抽象化，X1，X2，…，Xn，其中 Xi 取0或1，表示第 i 个物品选或不选，Vi表示第 i 个物品的价值，Wi表示第 i 个物品的体积（重量）；
- 约束条件：物品的总重量小于等于背包的容量。
- 定义二维数组res[i][j]表示前i件物品最佳组合的价值，j表示当前背包容量。
- 寻找递推关系式；当前物品有两种可能，第一，背包容量比该物品的重量小，装不下，此时的价值和前i-1个价值是一样的。res[i][j] = res[i-1][j]；第二种，当前背包的容量还可以装下该物品，但是装了不一定达到当前的最大价值，所以需要比较装该物品后的价值和不装的价值那个大，两者取最大值。res[i][j] = Math.max(res[i-1][j], res[i-1][j-weights[i]] + values[i])。
- 因此动态转移方程是：当j<W[i],res[i][j] = res[i-1][j]；
当j>W[i]，res[i][j]=max - 填表，记得初始化边界条件，当背包容量为0时，res[i][j]=0，当没有物品时，也即是i=0，最大价值也是0.
代码实现
1. public class ZeroOnePackage {
2. static int weights[] = {0,2,3,4,5,9};
3. static int values[] = {0,3,4,5,8,10};
4. static int N = 5;
5. static int C = 20;
6. static int res[][] = new int[N + 1][C + 1];
7.
8. public static void main(String[] args) {
9.
10. int res = zeroOne(21 ,6, weights, values);
11. System.out.println("背包所能容纳物品的最大价值是： "+res);
12. }
13. public static int zeroOne(int C, int N, int[] weights, int[] values) {
14. // 防止无效输入
15. if ((N < 0) || (weights.length != values.length)) {
16. return 0;
17. }
18. //0-1背包问题 C代表当前背包的容量，N代表当前有几件物品
19. for (int i = 1; i < N; i++) {
20. for (int j = 1; j < C; j++) {
21. //如果当前背包容量小于物品重量，那就返回前一个物品的最大价值
22. if (j < weights[i]) {
23. res[i][j] = res[i - 1][j];
24. } else {
25. //如果有容量，有两种选择，一个是装，一个不装，不装代表是上一个物品的最大容量，
26. // 装的话当前背包容量-当前物品重量 前i-1物品的总价值+当前物品价值
27. res[i][j] = Math.max(res[i-1][j], res[i-1][j-weights[i]] + values[i]);
28. }
29.
30. }
31. }
32. //格式化输出这张表，行代表第i件物品，列代表当前背包的容量
33. for (int i=1;i<N;i++){
34. for (int j = 1; j < C; j++) {
35. System.out.format("%d\t",res[i][j]);
36. }
37. System.out.println();
38. }
39. return res[N-1][C-1];
40. }
41. }
结果校验
在https://augustineaykara.github.io/Knapsack-Calculator/ 可视化背包问题的网站上，将测试数据输入，直接显示表格以及结果。
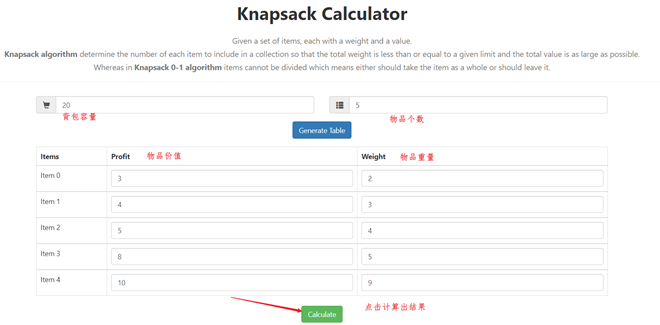
很显然，最终显示的结果与我们通过代码计算出的结果一致，说明算法没有问题。
算法时间复杂度O(nc)，空间复杂度O(nc)。
