TF-IDF算法

TF-IDF

1、概念

TF：term frequency，指一个词项在当前文档中出现的次数
IDF：invert document frequency，逆文档频率 ${idf=log\frac N n}$ ，其中 $N$ ：集合中文档数量； $n$ ：包含词项的文档数量

TF与当前文档有关，IDF与整个文档集合有关

举个例子，有以下文档集合， $N=4$

doc1: 苹果手机 apple iPhone 11 128G
doc2：苹果手机 apple iPhone 12 256G
doc3：小米手机 小米11
doc4：手机壳 适用于华为手机

计算apple，小米，手机三个词在doc1中的TF和整个文档集合中的IDF值：

词项	TF(doc1)	IDF
apple	1	$log\frac 4 2=1$
小米	0	$log\frac 4 1=2$
手机	1	$log\frac 4 4=0$

2、计算公式

T F * I D F = \frac{f r e q (T, D)}{s i z e (D)} * - l o g_{2} \frac{d f (T)}{N}

$TF*IDF = \frac {freq(T,D)} {size(D)} * -log_2\frac {df(T)} {N}$

$T$ ：词项
$D$ ：文档
$freq(T,D)$ ：词项 $T$ 在文档 $D$ 中出现的次数
$size(D)$ ：文档 $D$ 包含的词项总数
$df(T)$ ：文档集合中包含词项 $T$ 的文档总数
$N$ ：集合中的文档总数

参考文献： I. H. Witten, G. W. Paynteer, E. Frank, et al. KEA: Practical automatic keyphrase extraction. The 4th ACM Conference on Digital Libraries, Berkeley: ACM Press, 1999: 254-256.

从公式可以看出 ①词项在文档中出现的次数越多，得分越高；②包含词项的文档越多，得分越低。即，在文档中高频、集合中低频的词得分高。

3、如何提出的？

TF：从1957年开始在检索领域使用
IDF：1972年由英国科学院院士克伦·施拜克·琼斯（Karen Sprck Jones）提出

克伦·施拜克·琼斯（Karen Sprck Jones，1935年8月26日-2007年4月4日），女，英国科学院院士。剑桥大学毕业，获哲学博士学位。1972年提出的逆文本频率指数（IDF）的概念，而IDF是互联网搜索引擎普遍采用的思路。为谷歌搜索引擎日后的成就做出贡献。曾任英国科学院副院长。获得过包括2004年“国际计算语言学学会终身成就奖”和2007年“英国计算机学会勒芙蕾丝奖章”等7个重要奖项。

文章：Jones K S. A Statistical Interpretation of Term Specificity and Its Application in Retrieval[J]. Journal of Documentation, 1972, 28(1): 11-21.

作者通过一些实验发现 高频词对应高召回率，低频词对应高准确度，为了得到准确度和召回率都高的结果，就需要将高频词和低频词结合起来。

从用户的角度而言，准确度比召回率更重要，因此低频词重要性要高于高频词。

接下来作者统计了集合中每个词对应的文档数量，绘制了频率曲线，发现曲线和Zipf定律类似。

Zipf定律：

参考书籍：Human behavior and the principle of least effort: An introduction to human ecology
中文书名《最省力原则：人类行为生态学导论》

詹姆斯·乔伊斯的小说《尤利西斯》有260430个词，包含29899个不同的词语。按照这些不同词语出现的频率进行降序排序，每个不同词语的实际频率以及伴随该频率出现的不同序列r。例如，频率位居第10的词语（r=10）出现了2 653次（f=2 653），或者频率位居第100的词语（r=100）出现了265次（f=265）。

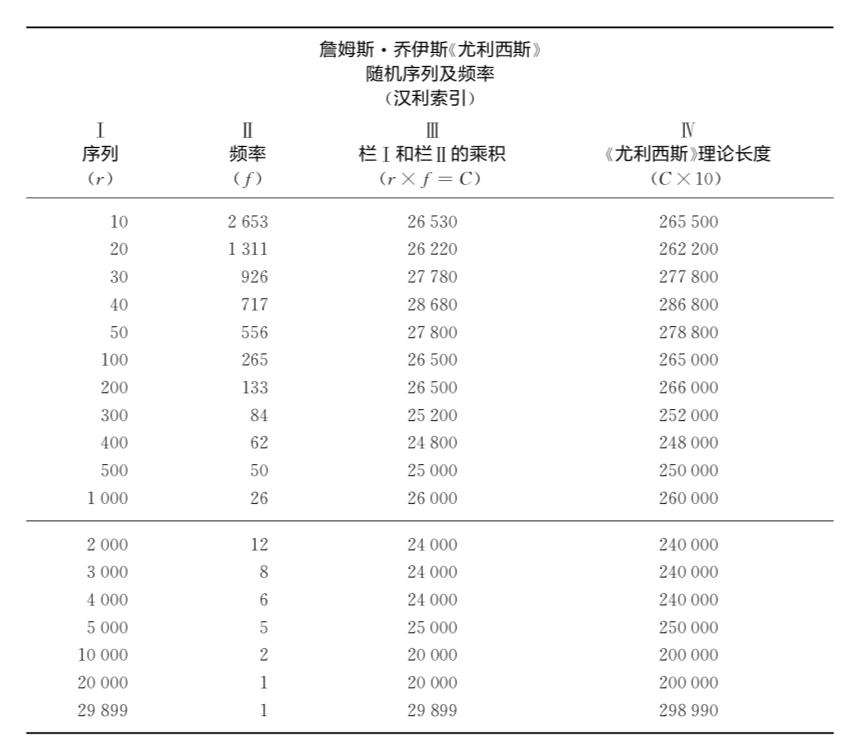
乔伊斯的《尤利西斯》中r与f之间的关系并非杂乱无章。因为如果我们将表1第Ⅰ栏中每个序列r乘以第Ⅱ栏中相应的频率f，我们就会得出第Ⅲ栏中的乘积C，所有不同序列的乘积差不多是同样大小，该乘积如第Ⅳ栏所见代表了构成《尤利西斯》总规模的260 430个连续词语的1/10。其实，就表1而言，我们所发现《尤利西斯》中不同词语的数量及其使用频率之间有着清晰的相互联系，即它们俩接近一个等轴双曲线的简单方程式：
$f*r = C$

对 $f*r = C$ 两边除以 $r$ 后取对数： $logf = -logr + logC$

使用对数坐标系： $y = -x + b$ ，即在对数坐标系中应该与 $x$ 轴负方向呈45°夹角。

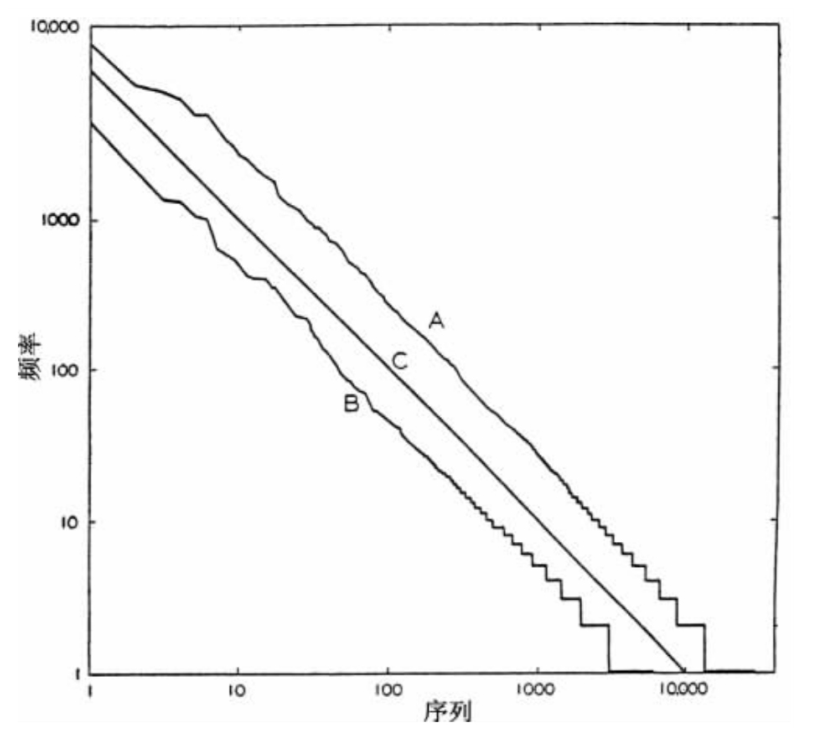
如下图1，曲线A表示《尤利西斯》的数据，曲线B为埃尔德里奇（R.C.Eldridge）分析美国报纸联合实例总计43 989个词语中6 002个不同词语的数据，曲线C是45°斜率的理想曲线。

idf的作者根据统计的每个词对应的文档数量的频率曲线，结合Zipf定律，提出

f (n) = m, 2^{m - 1} < n < 2^{m}

$f(n) = m, 2^{m-1} < n < 2^m$

term的权重 $w = f(N) - f(n) + 1$ ，其中 $N$ 表示集合中的文档数量， $n$ 表示包含term的文档数量。

多个term的权重则为每个term的权重之和。

若公式 $f(n) = m, 2^{m-1} < n < 2^m$ 不对 $m$ 向上取整的话，term的权重可写为 $w=logN - logn + 1= -log\frac n N + 1$

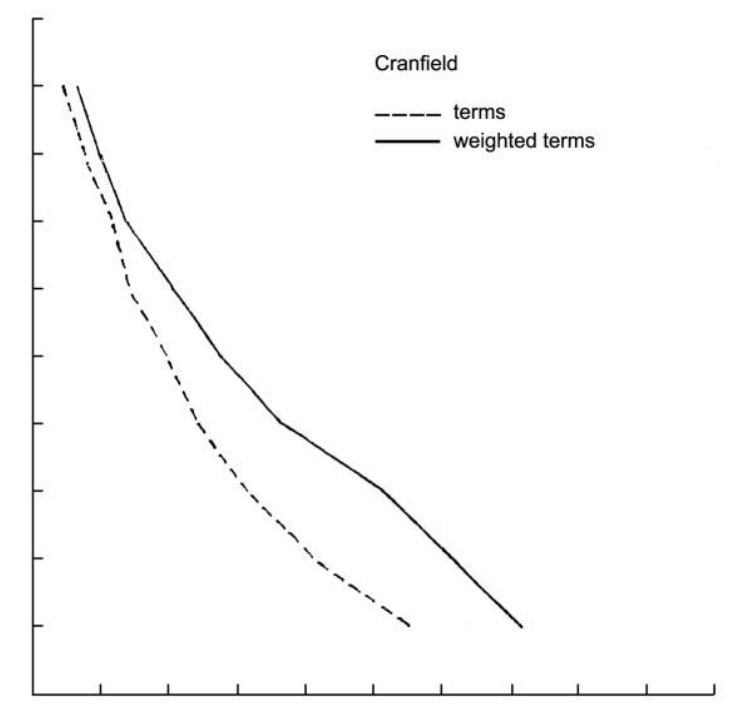
作者对使用IDF加权和不加权两种搜索结果进行对比，如下图2，可以发现使用IDF加权的结果完全包含了不加权的曲线，即，使用IDF加权的方式更优。

4、ES中的TF-IDF计算公式

官网地址
https://www.elastic.co/guide/en/elasticsearch/guide/2.x/practical-scoring-function.html
https://www.elastic.co/guide/en/elasticsearch/guide/2.x/scoring-theory.html#tfidf

s c o r e (q, d) = q u e r y N o r m (q) * c o o r d (q, d) * \sum_{t i n q} [t f (t i n d) * i d f (t)^{2} * b o o s t (t) * n o r m (t, d)]

$score(q,d)=queryNorm(q)*coord(q,d)*\sum_{t\,in\,q}[tf(t\,in\,d)*idf(t)^2*boost(t)*norm(t,d)]$

各项因子含义如下：
$q$ ：query
$d$ ：document
$queryNorm(q)$ ：query normalization factor 查询标准化因子
目的：方便与另一个查询结果比较而作的标准化，但是并不好用，score的唯一目的是按照正确的相关性对结果排序，不应该尝试比较不同查询的相关性分数。对于给定的查询 $q$ 而言，是定值（若文档集合不变）

q u e r y N o r m (q) = \frac{1}{\sqrt{\sum_{t i n q} i d f (t)^{2}}}

$queryNorm(q)=\frac 1 {\sqrt{\sum_{t\,in\,q}idf(t)^2}}$

： $idf(t)=1+log\frac N {n+1}$
$N$ ：集合中文档总数； $n$ ：包含词 $t$ 的文档数量
$coord(q,d)$ ：协调因子。文档中出现的查询词越多，匹配的概率越大，得分越高

c o o r d (q, d) = \frac{文 档 中 出 现 的 查 询 词 个 数}{查 询 词 总 数}

$coord(q,d)=\frac {文档中出现的查询词个数} {查询词总数}$

$tf(t\,in\,d)$ ：词在文档中出现的次数 $tf(t,in,d)=\sqrt{t在d中出现的次数}$
$boost(t)$ ：查询 $q$ 指定的 $boost$ ，默认为1
：字段长度范数，字段越短，得分越高 $norm(t,d)=\frac 1 {d中对应字段的长度}$

特点

倾向于短字段
倾向于集合中罕见词
文档中频率高的词
文档包含的查询词越多，得分越高
设置的boost值

posted @ 2023-02-01 10:57 dedication 阅读(1171) 评论(0) 编辑收藏举报

dedication

TF-IDF算法

TF-IDF

1、概念

2、计算公式

3、如何提出的？

4、ES中的TF-IDF计算公式

公告

搜索

常用链接

我的标签

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论