神经网络中注意力机制概述

总结来自这篇论文的第7章

注意力机制

注意力机制是一种在编码器-解码器结构中使用到的机制, 现在已经在多种任务中使用:

• 机器翻译(Neural Machine Translation, NMT)
• 图像描述(Image Captioning (translating an image to a sentence))
• 文本摘要(Summarization(translating to a more compact language))

而且也不再局限于编码器-解码器结构, 多种变体的注意力结构, 应用在各种任务中.

总的来说, 注意力机制应用在:

• 允许解码器在序列中的多个向量中, 关注它所需要的信息, 是传统的注意力机制的用法. 由于使用了编码器多步输出, 而不是使用对应步的单一定长向量, 因此保留了更多的信息.
• 作用于编码器, 解决表征问题(例如Encoding Vector再作为其他模型的输入), 一般使用自注意力(self-attention)

1. 编码器-解码器注意力机制

1.1 编码器-解码器结构

如上图, 编码器将输入嵌入为一个向量, 解码器根据这个向量得到输出. 由于这种结构一般的应用场景(机器翻译等), 其输入输出都是序列, 因此也被称为序列到序列的模型Seq2Seq.

对于编码器-解码器结构的训练, 由于这种结构处处可微, 因此模型的参数\(\theta\)可以通过训练数据和最大似然估计得到最优解, 最大化对数似然函数以获得最优模型的参数, 即:

\[\arg\max\limits_{\theta}\{\sum\limits_{(x,y)\in{corpus}}\log{p(y|x;\theta)}\} \]

这是一种端到端的训练方法.

1.2 编码器

原输入通过一个网络模型(CNN, RNN, DNN), 编码为一个向量. 由于这里研究的是注意力, 就以双向RNN作为示例模型.

对于每个时间步\(t\), 双向RNN编码得到的向量\(h_t\)可以如下表示:

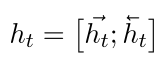
1.3 解码器

这里的解码器是单向RNN结构, 以便在每个时间点上产生输出, 行程序列. 由于解码器仅使用最后时间步\(T\)对应的编码器的隐藏向量\(h_{T_x}\), \(T_x\)指的是当前样本的时间步长度(对于NLP问题, 经常将所有样本处理成等长的). 这就迫使编码器将更多的信息整合到最后的隐藏向量\(h_{T_x}\)中.

但由于\(h_{T_x}\)是单个长度一定的向量, 这个单一向量的表征能力有限, 包含的信息量有限, 很多信息都会损失掉.

注意力机制允许解码器在每一个时间步\(t\)处考虑整个编码器输出的隐藏状态序列\((h_1, h_2, \cdots, h_{T_x})\), 从而编码器将更多的信息分散地保存在所有隐藏状态向量中, 而解码器在使用这些隐藏向量时, 就能决定对哪些向量更关心.

具体来说, 解码器生产的目标序列\((y_1, \cdots, y_{T_x})\)中的每一个输出(如单词)\(y_t\), 都是基于如下的条件分布:

\[P[y_t|\{y_1,\cdots,y_{t-1}\},c_t]=softmax(W_s \tilde{h}_t) \]

其中\(\tilde{h}_t\)是引入注意力的隐藏状态向量(attentional hidden state), 如下得到:

\[\tilde{h}_t=\tanh(W_c[c_t;h_t]) \]

\(h_t\)为编码器顶层的隐藏状态, \(c_t\)是上下文向量, 是通过当前时间步上下文的隐藏向量计算得到的, 主要有全局和局部两种计算方法, 下午中提到. \(W_c\)和\(W_s\)参数矩阵训练得到. 为了式子的简化没有展示偏置项.

1.4 全局注意力

通过全局注意力计算上下文向量\(c_t\)时, 使用整个序列的隐藏向量\(h_t\), 通过加权和的方式获得. 假设对于样本\(x\)的序列长度为\(T_x\), \(c_t\)如下计算得到:

\[c_t=\sum\limits_{i=1}^{T_x}\alpha_{t,i}h_i \]

其中长度为\(T_x\)的校准向量alignment vector \(\alpha_t\)的作用是在\(t\)时间步, 隐藏状态序列中的所有向量的重要程度. 其中每个元素\(\alpha_{t,i}\)的使用softmax方法计算:

\[\alpha_{t,i}=\frac{\exp(score(h_t, h_i))}{\sum\limits_{j=1}^{T_x}\exp(score(h_t, h_j))} \]

值的大小指明了序列中哪个时间步对预测当前时间步\(t\)的作用大小.

score函数可以是任意的比对向量的函数, 一般常用:

• 点积: \(score(h_t, h_i)=h_t^Th_i\)

  这在使用全局注意力时有更好的效果

• 使用参数矩阵:

  \(score(h_t, h_i)=h_t^TW_{\alpha}h_i\)

  这就相当于使用了一个全连接层, 这种方法在使用局部注意力时有更好的效果.

全局注意力的总结如下图:

1.5 局部注意力

全局注意力需要在序列中所有的时间步上进行计算, 计算的代价是比较高的, 可以使用固定窗口大小的局部注意力机制, 窗口的大小为\(2D+1\). \(D\)为超参数, 为窗口边缘距离中心的单方向距离. 上下文向量\(c_t\)的计算方法如下:

\[c_t=\sum\limits_{i=p_t-D}^{p_t+D}\alpha_{t,i}h_i \]

可以看到, 只是考虑的时间步范围的区别, 其他完全相同. \(p_t\)作为窗口的中心, 可以直接使其等于当前时间步\(t\), 也可以设置为一个变量, 通过训练获得, 即:

\[p_t=T_x\sigma(v_p^T\tanh(W_ph_t)) \]

其中\(\sigma\)为sigmoid函数, \(v_p\)和\(W_p\)均为可训练参数. 因此这样计算得到的\(p_t\)是一个浮点数, 但这并没有影响, 因为计算校准权重向量\(\alpha_t\)时, 增加了一个均值为\(p_t\), 标准差为\(\frac{D}{2}\)的正态分布项:

\[\alpha_{t,i}=\frac{\exp(score(h_t, h_i))}{\sum\limits_{j=1}^{T_x}\exp(score(h_t, h_j))}\exp(-\frac{(i-p_t)^2}{2(D/2)^2}) \]

当然, 这里有\(p_t\in\mathbb{R}\cap[0, T_x]\), \(i\in\mathbb{N}\cap[p_t-D, p_t+D]\). 由于正态项的存在, 此时的注意力机制认为窗口中心附近的时间步对应的向量更重要, 且与全局注意力相比, 除了正态项还增加了一个截断, 即一个截断的正态分布.

局部注意力机制总结如下图:

2. 自注意力

2.1 与编码器-解码器注意力机制的不同

最大的区别是自注意力模型没有解码器. 因此有两个最直接的区别:

• 上下文向量\(c_t\)在seq2seq模型中, \(c_t=\sum\limits_{i=1}^{T_x}\alpha_{t,i}h_i\), 用来组成解码器的输入$$\tilde{h}_t=\tanh(W_c[c_t;h_t])$$, 但由于自注意力机制没有解码器, 所以这里就直接是模型的输出, 即为\(s_t\)
• 在计算校准向量\(\alpha_t\)时, seq2seq模型使用的是各个位置的隐藏向量与当前隐藏向量的比较值. 在自注意力机制中, 校准向量中的每个元素由每个位置的隐藏向量与当前时间步\(t\)的平均最优向量计算得到的, 而这个平均最优向量是通过训练得到的

2.2 自注意力机制实现

首先将隐藏向量\(h_i\)输入至全连接层(权重矩阵为\(W\)), 得到\(u_i\):

\[u_i=\tanh(Wh_i) \]

使用这个向量计算校正向量\(\alpha_t\), 通过softmax归一化得到:

\[\alpha_{t,i}=\frac{\exp(score(u_i, u_t))}{\sum\limits_{j=1}^{T_x}\exp(score(u_j, u_t))} \]

这里的\(u_t\)是当前时间步\(t\)对应的平均最优向量, 每个时间步不同, 这个向量是通过训练得到的.

最后计算最后的输出:

\[s_t=\sum\limits_{i=1}^{T}a_{t, i}h_i \]

一般来说, 在序列问题中, 只关心最后时间步的输出, 前面时间步不进行输出, 即最后的输出为\(s=s_T\)

2.3 层级注意力

如下图, 对于一个NLP问题, 在整个架构中, 使用了两个自注意力机制: 词层面和句子层面. 符合文档的自然层级结构:

词->句子->文档. 在每个句子中, 确定每个单词的重要性, 在整片文档中, 确定不同句子的重要性.