论文阅读 SNAPSHOT ENSEMBLES

引入

1. 随机梯度下降的特点

随机梯度下降法(Stochastic Gradient Descent)作为深度学习中主流使用的最优化方法, 有以下的优点:

• 躲避和逃离假的鞍点和局部极小点的能力

这篇论文认为, 这些局部极小也包含着一些有用的信息, 能够帮助提升模型的能力.

2. 局部极小的意义

神经网络的最优化一般来说, 不会收敛在全局最小上, 而是收敛在某个局部极小上. 这些局部极小有着好和坏的区别. 而对于好坏的区分, 一般认为:

• 局部极小有着平坦的区域flat basin, 这些点对应模型的泛化性比较好, 是更好的局部极小

3. SGD与局部极小

SGD在最优化过程中, 会避免陡峭的局部极小, 这是因为:

• 计算得到的梯度是由mini-batch得到的, 因此是不精确的
• 当学习率learning rate比较大的时候, 沿着这个不精确的梯度的某一步移动不会到达具有陡峭局部的极小点

这是SGD在最优化过程中的优点, 避免了收敛域陡峭的局部极小.

但当学习率比较小的时候, SGD方法又趋向于收敛到最近的局部极小.

SGD的这两种截然不同的行为, 会在训练的不同阶段表现出来:

• 初始阶段使用大的学习率, 快速移动到靠近平坦局部极小的区域
• 当搜索进行到没有提升的阶段, 降低学习率, 引导搜索收敛到最终的局部极小里面

4. 模型训练与局部极小

局部极小的数量, 随着模型中参数的增多, 呈指数式增加. 因此神经网络中的局部极小数不胜数. 同一个模型, 因为初始化的不同, 或者训练样本batch顺序的不同, 会收敛到不同的局部极小中去, 因此模型的表现也就会有差异.

往往在实际中, 不同的局部极小产生的最终的总误差近似, 但是实际上, 不同局部极小对应的不同模型在预测时会产生不同的错误. 这种模型之间的差异在进行Ensemble(投票, 平均)会被利用到, 往往对最终的预测结果都有提升, 因此在各种比赛中, 多模型Ensemble被广泛使用.

5. Ensemble与神经网络

由于神经网络训练的耗时, 导致多模型的Ensemble在深度学习领域应用不如传统的机器学习方法广泛. 因为用于Ensemble的每个基模型, 都是单独训练的, 往往单个模型的训练就比较耗时了, 因此这种提升模型表现的方法成本是相当高的.

这篇论文提出了一种方法, 不需要增加额外的训练消耗, 通过一次训练, 得到若干个模型, 并对这些模型进行Ensemble, 得到最终的模型.

原理

1. 概括

首先, 在对神经网络使用SGD方法进行训练时, 利用SGD方法能够收敛和逃离局部极小的特点, 在一次训练过程中, 使模型\(M\)次收敛于不同的局部极小, 每次收敛, 都代表这一个最终的模型, 我们将此时的模型进行保存. 然后使用一个较大的学习率逃离此时的局部极小.

在论文中, 对学习率的控制使用了一种余弦函数, 这种函数表现为:

• 急剧提升学习率
• 在某次训练过程中, 学习率迅速下降

这种训练方式就像在最优化路程中, 截取了几个快照Snapshot, 因此命名为Snapshot Ensembling. 下图中的右半部分就是对这种方法的图像表现.

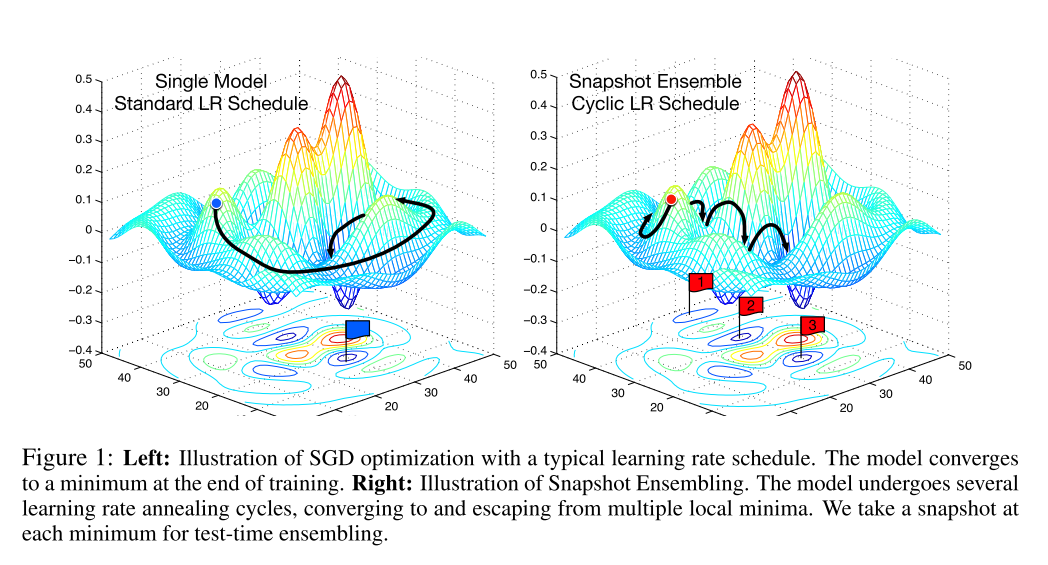
2. 神经网络的隐式与显式Ensemble

各种Dropout技术是一种隐式的Ensemble技术, 在训练的时候, 随机地将隐藏层中的部分结点, 且在每次训练过程中隐藏的结点都不相同, 而在训练时则使用所有结点.

因此, 在使用Dropout技术训练的过程中, 通过随机地去除隐藏层的结点, 创建了无数个共享权重的模型. 这些模型在预测的时候, 被隐式地Ensemble在一起.

这篇论文提出的Snapshot Ensemble则是显式地将多个不共享权值的模型组合在一起, 达到提升的效果.

3. 详述

总的来说, Snapshot Ensemble就是在一次训练(最优化)过程中, 在最终收敛之前, 访问多个局部极小, 在每个局部极小保存快照即作为一个模型, 在预测的使用使用所有保存的模型进行预测, 最后取平均值作为最终结果.

而这些模型保存点(快照点)不是随意选取的, 我们希望:

• 有尽量小的误差
• 每个模型误分类的样本尽量不要重复, 保证模型的差异性

这就需要在最优化过程中进行一些特别的操作.

观察标准的最优化路径, 通常来说, 开发集的误差只有在学习率下调之后才会急剧下降, 按照正常的学习率下降策略, 上述情况往往会在很多个Epoch之后才会出现.

然而, 很早地降低学习率继续训练, 对最后的误差并不会造成大的影响, 却极大地提高了训练的效率, 使得模型在较少的epoch轮数迭代后就达到局部极小成为了可能.

因此, 论文中采用了Cyclic Cosine Annealing方法, 很早地就下调了学习率, 使训练尽快地到达第一个局部极小, 得到第一个模型. 然后提升学习率, 扰乱模型, 使得模型脱离局部极小, 然后重复上述步骤若干次, 直到获取指定数量的模型.

而学习率的变化, 论文中使用如下的函数:

\[\alpha(t)=f(\mod(t-1, \lceil T/M \rceil)) \]

其中, \(t\)是迭代轮数, 这里指的是batch轮数; \(T\)是总的batch数量; \(f\)是单调递减函数; \(M\)是循环的数量, 也就是最终模型的数量. 换句话说, 我们将整个训练过程划分成了\(M\)个循环, 在每个循环的开始阶段, 使用较大的学习率, 然后退火到小的学习率. \(\alpha=f(0)\)给予模型足够的能量脱离局部极小, 而较小的学习率\(\alpha=f(\lceil T/M \rceil)\)又能使模型收敛于一个表现较好的局部极小.

论文中使用如下的shifted cosine function:

\[\alpha(t)=\frac{\alpha_0}{2}(\cos(\frac{\pi\mod(t-1,\lceil T/M \rceil)}{\lceil T/M \rceil})+1) \]

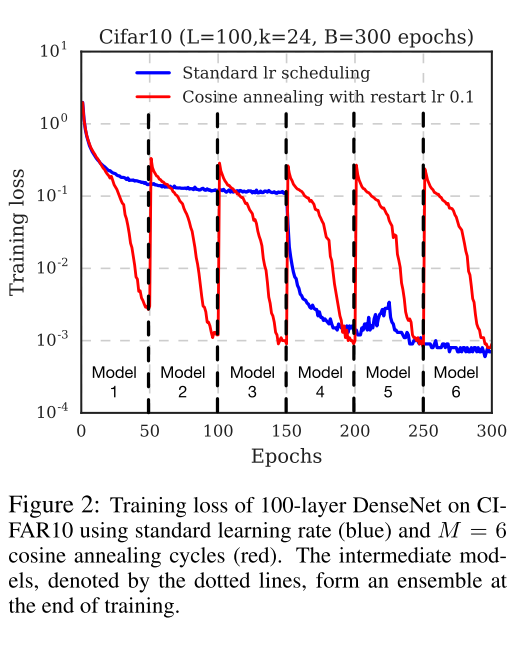
\(\alpha_0\)是初始的学习率, 而\(\alpha=f(\lceil T/M \rceil)\approx0\)这保证了最小的学习率足够小. 每个batch作为一次循环(而不是每个epoch). 以下是整个学习过程的表现.