论文阅读笔记: Natural Language Inference over Interaction Space
这篇文章提出了DIIN(DENSELY INTERACTIVE INFERENCE NETWORK)模型. 是解决NLI(NATURAL LANGUAGE INFERENCE)问题的很好的一种方法.
模型结构
首先, 论文提出了IIN(Interactive Inference Network)网络结构的组成, 是一种五层的结构, 每层的结构有其固定的作用, 但是每层的实现可以使用任意能达到目的的子模型. 整体的结构如下图:
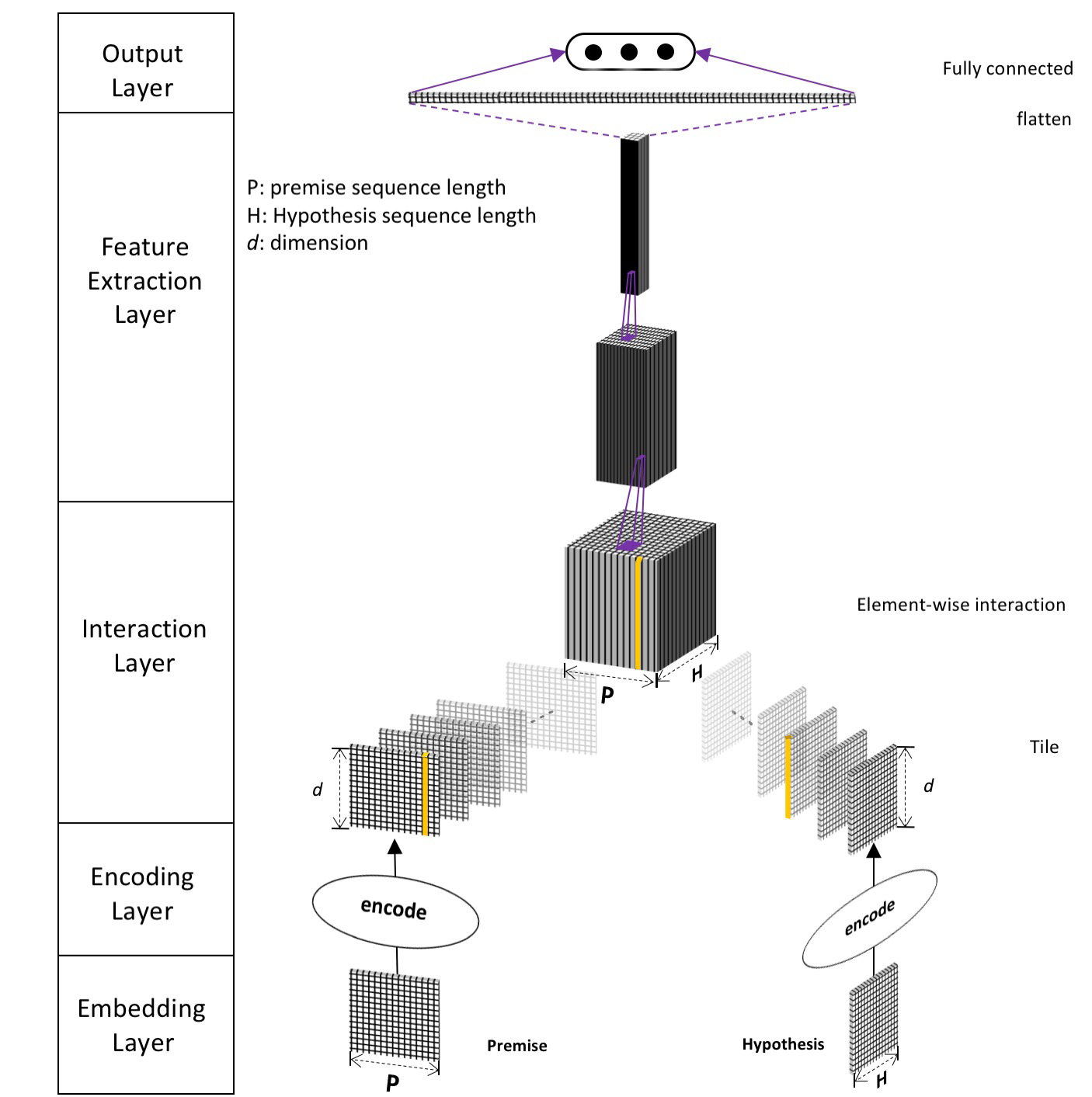
模型结构从上到下依次为:
- Embedding Layer: 常见的对
word进行向量化的方法, 如word2vec,GloVe,fasttext等方法. 此外文章中还使用了两种方法对char进行编码, 对每个word中的char进行编码, 并拼接上char的特征, 组合成一个向量, 拼接在word embedding vector上. 这样就包含了更多的信息. 具体的方法在后文讲到. - Encoding Layer: 对句子进行编码, 可以用多种模型进行编码, 然后将他们编码的结果合并起来, 从而获得更多方面的关于句子的信息.
- Interaction Layer: 在这一层将两个句子的信息进行交互. 可以采用对两个句子中的单词
word-by-word的相互作用的方法. 相互作用的方法也有很多选择. - Feature Extraction Layer: 从上层得到两个句子相互作用产生的
Tensor, 使用一些常见的CNN网络进行处理, 如AlexNet,VGG,Inception,ResNet,DenseNet等. 注意这里使用的是处理图像的2-D的卷积核, 而不是文本常用的1-D卷积核. 使用方法见下文. - Output Layer: 将特征转换为最终结果的一层. 只需要设置好输出类的数量即可.
DIIN模型结构
具体的解析DIIN模型每层的结构.
Embedding Layer
这里将三种生成word的方法拼接起来: word embedding, character feature, syntactical features.
-
word embedding论文中使用的是通过
GloVe预训练好的向量. 而且, 论文中提到在训练时, 要打开word embedding的训练, 跟随着任务一起训练. -
character feature这里指的是对一个
word中的char进行自动的feature.首先使用
char embedding对每个char进行向量化, 然后对char向量进行1-D的卷积, 最后使用MaxPool得到这一个单词对应的char特征向量.使用
keras实现如下:character_embedding_layer = TimeDistributed(Sequential([ Embedding(input_dim=100, output_dim=char_embedding_size, input_length=chars_per_word), Conv1D(filters=char_conv_filters, kernel_size=char_conv_kernel_size), GlobalMaxPooling1D() ]), name='CharEmbedding') character_embedding_layer.build(input_shape=(None, None, chars_per_word)) premise_char_embedding = character_embedding_layer(premise_char_input) hypothesis_char_embedding = character_embedding_layer(hypothesis_char_input) -
syntactical features添加这种的目的是为OOV(out-of-vocabulary)的
word提供额外补充的信息. 论文中提到的方法有:- part-of-speech(
POS), 词性特征, 使用词性的One-Hot特征. - binary exact match(
EM)特征, 指的是一个句字中的某个word与另一个句子中对应的word的词干stem和辅助项lemma相同, 则是1, 否则为0. 具体的实现和作用在论文中有另外详细的阐述.
- part-of-speech(
通过这三种方法, 就得到了premise句子\(P\in{\mathbb{R}^{p\times{d}}}\)和hypothesis句子\(H\in{\mathbb{R}^{h\times{d}}}\)的表示方法, 其中\(p\)和\(h\)分别表示premise句子和hypothesis句子的长度, \(d\)表示最终每个单词向量的长度.
对于对char编码过程中使用到的Conv1D, 两个句子共享同样的参数, 这是毋庸置疑的.
Encoding Layer
在这一层中, premise和hypothesis会经过一个两层的神经网络, 得到句子中的每一个word将会用一种新的方式表示. 然后将转换过的表示方法传入到一个self-attention layer中. 这种attenion结构在解决NLI问题的模型中经常出现, 目的是考虑word的顺序和上下文信息. 以premise为例:
假设\(\hat{P}\in{\mathbb{R}^{p\times{d}}}\)是经过转换后的premise句子, \(\hat{P}_i\)是时序\(i\)位置上的word新的向量. 同理, \(\hat{H}\in{\mathbb{R}^{h\times{d}}}\)是转换后的新的hypothesis句子.
在转换时, 我们需要考虑当前单词与它的上下文之间的关系, 文中使用的方法是self-attention layer, 具体来说就是每个时间上经过编码后新的向量, 由整个句子中所有位置上的原向量考虑权重地加和产生. 而两个单词向量之间的权值就要借助attention weight来得到了. 以premise句子为例, 整个过程如下:
-
对于
premise句子的任意两个向量\(\hat{P}_{i}\)和\(\hat{P}_{j}\), 通过\([\textbf{a};\textbf{b};\textbf{a}\cdot \textbf{b}]\)的形式组成一个交互的向量. 原向量的长度为\(d\), 则新向量的长度为\(3d\). 则长度为\(p\)的句子经过此步, 就会得到\((p,p,3d)\). -
使用共享的
attention weight\(\textbf{w}_a\)与\([\textbf{a};\textbf{b};\textbf{a}\cdot \textbf{b}]\)进行点乘. \(\textbf{w}_a\)的是长度为\(3d\)的向量. 所有的word之间共享这一参数向量. 因此点乘的结果为一个形状为\((p,p)\)的矩阵, 用\(A\)表示, \(A_{ij}\)则是两个word之间的关系值. -
使用
softmax的方法计算权重, 即对于每一行\(i\), 对应的新的向量为:\[\bar{P}_i=\sum\limits_{j=1}^{p}\frac{\exp(A_{ij})}{\sum_{k=1}^{p}\exp(A_{kj})}\hat{P}_{j} \]每个词的新向量都会考虑句子中其他所有的向量.
以上三步的代码类似于:
''' Alpha ''' # P # (batch, p, d) mid = broadcast_last_axis(P) # (batch, p, d, p) up = K.permute_dimensions(mid, pattern=(0, 3, 2, 1)) # (batch, p, d, p) alphaP = K.concatenate([up, mid, up * mid], axis=2) # (batch, p, 3d, p) A = K.dot(self.w_itr_att, alphaP) # (batch, p, p) ''' Self-attention ''' # P_itr_attn[i] = sum of for j = 1...p: # s = sum(for k = 1...p: e^A[k][j] # ( e^A[i][j] / s ) * P[j] --> P[j] is the j-th row, while the first part is a number # So P_itr_attn is the weighted sum of P # SA is column-wise soft-max applied on A # P_itr_attn[i] is the sum of all rows of P scaled by i-th row of SA SA = softmax(A, axis=2) # (batch, p, p) itr_attn = K.batch_dot(SA, P) # (batch, p, d) -
然后将新得到的\(d\)维向量和原本的\(d\)维向量合并在一起组成\(2d\)向量, 再传入
semantic composite fuse gate(fuse gate), 这种把encoding后的向量和原特征向量拼在一起在传入下一层模型的方法, 如同skip connection(类比于ResNet).fuse gate结构如下:\[z_i=\tanh(W_1^T[\hat{P}_i;\bar{P}_i]+\textbf{b}_1) \]\[r_i=\sigma(W_2^T[\hat{P}_i;\bar{P}_i]+\textbf{b}_2) \]\[f_i=\sigma(W_3^T[\hat{P}_i;\bar{P}_i]+\textbf{b}_3) \]\[\tilde{P}_i=\textbf{r}_i \cdot \hat{P}_i + \textbf{f}_i \cdot \textbf{z}_i \]这里的\(W_1\), \(W_2\), \(W_3\)的形状为\((2d,d)\), \(b_1\), \(b_2\), \(b_3\)为长度为\(d\)的向量. 都是可训练的参数. \(\sigma\)为
sigmoid函数.
需要注意的是, 在这一层中, premise和hypothesis两个句子是不共享参数的, 但是为了让两个句子的参数相近, 两个句子在相同位置上的变量, 会对他们之间的差距做L2正则惩罚, 将这种惩罚计入总的loss, 从而在训练过程中, 保证了参数的近似.
那么对于premise和hypothesis两个句子来源一个分布的情况, 是否可以共用一组参数呢? 需要进一步的实验.
Interaction Layer
对两个句子的word进行编码之后, 就要考虑两个句子相互作用的问题了. 对于长度为\(p\)的premise和长度为\(h\)的hypothesis, 对于他们的每个单词\(i\)和\(j\), 将代表它们的向量逐元素点乘, 这样就得到了一个形状为\((p, h, d)\)的两个句子相互作用后的结果. 可以把他们认为是一个2-d的图像, 有d个通道.
Feature Extraction Layer
由于两个句子相互作用产生了一个2-d的结果, 因此我们可以通过使用那些平常用在图像上的CNN方法结构, 来提取特征, 例如ResNet效果就很好. 但考虑到模型的效率, 与参数的多少, 论文中使用了DenseNet这种结构. 这种结构的具体论文参见Densely Connected Convolutional Networks. 这一层整体的过程如下:
-
上一步得到的结果我们记为\(I\), 形状为\((p, h, d)\). 首先使用一个\(1\times{1}\)的卷积核, 按一定的缩小比例\(\eta\), 将现有的\(d\)层通道缩小为\(floor(d \times{\eta})\).
-
再将得到的结果传入到一个三层结构中, 三层的结构完全相同. 每一层由一对
Dense block和transition block组成. 两种block是串联关系.-
DenseNet本身是由n层的\(3\times{3}\)的卷积层组成, 中间没有池化层. 每层的输出通道数量是一样的, 记为growth rate. 且每层的输出, 都会并上这一层的输入, 作为下一层的输入. 这样也起到了类似于ResNet的skip效果. 代码如下:def __dense_block(self, x, nb_layers, growth_rate, dropout_rate=None, apply_batch_norm=False): for i in range(nb_layers): cb = self.__conv_block(x, growth_rate, dropout_rate, apply_batch_norm=apply_batch_norm) x = concatenate([x, cb], axis=self.concat_axis) return x, K.int_shape(x)[self.concat_axis] -
transition block这是一层简单的\(1\times{1}\)的卷积层, 目的是按照一定的比例压缩输出的通道. 这里的压缩比例跟上面的\(\eta\)是不相关的, 记为\(\theta\). 之后再在后面接上一个MaxPool, 考虑的范围是\(2\times{2}\)大小. 代码如下:def __transition_block(self, x, nb_filter, compression, apply_batch_norm): if apply_batch_norm: x = BatchNormalization(axis=self.concat_axis, epsilon=1.1e-5)(x) x = Conv2D(int(nb_filter * compression), (1, 1), padding='same', activation=None)(x) x = MaxPooling2D(strides=(2, 2))(x) return x
-
Output Layer
结果上面一层就使用2-d的方法得到了两个句子交互的特征. 然后把他们展平, 拼接到输出层的Dense上就可以. Dense的输出维度为类别的数量.
# Flatten if the shapes are known otherwise apply average pooling
try: x = Flatten()(x)
except: x = GlobalAveragePooling2D()(x)
x = Dense(classes, activation=activation)(x)
论文代码
在github上有使用keras实现的模型DIIN-in-Keras. 代码使用了自定义Model, Layer, Optimizer的方式实现了这个模型, 形式非常灵活, 值得借鉴学习.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号