集成学习简介
集成学习(ensemble learning),有时也被称为多分类器系统multi-classifier system)、基于委员会的学习(committee-based learning)等。可以说是现在非常火爆的机器学习方法了。它本身不是一个单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务。也就是我们常说的“博采众长”。集成学习可以用于分类问题集成,回归问题集成,特征选取集成,异常点检测集成等等,可以说所有的机器学习领域都可以看到集成学习的身影。本文就对集成学习的原理做一个简介。
1. 集成学习的结构
集成学习的一般结构:先产生一组“个体学习器”,再用某种策略将它们结合起来。如图1所示:
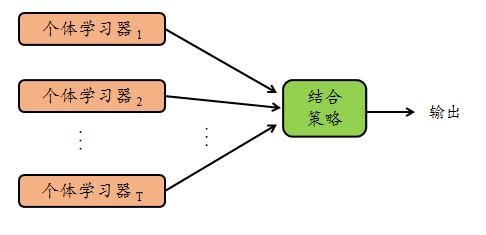
图1 集成学习示意图
显然,集成学习中有两个问题需要解决:
- 如何产生一组个体学习器;
- 如何选择一种结合策略。
我们的目的是通过有效的结合策略将这组个体学习器结合起来,获得比单一学习器显著优越的泛化性能。
2. 个体学习器
首先,集成学习的第一个问题就是如何产生一组个体学习器。个体学习器通常由一个现有的学习算法从训练数据产生,例如CART决策树算法、BP神经网络算法等,此时集成中只包含同种类型的个体学习器,例如"决策树集成"中全是决策树,"神经网络集成"中全是神经网络,这样的集成是"同质"的 (homogeneous)。同质集成中的个体学习器亦称"基学习器" (base learner), 相应的学习算法称为"基学习算法" (base learning algorithm)。集成也可包含不同类型的个体学习器,例如同时包含决策树和神经网络,这样的集成是"异质"的(heterogenous)。异质集成中的个体学习器由不同的学习算法生成,这时就不再有基学习算法;相应的,个体学习器一般不称为基学习器,常称为"组件学习器" (component learner) 或直接称为个体学习器。目前来说,同质个体学习器的应用是最广泛的,一般我们常说的集成学习的方法都是指的同质个体学习器。而同质个体学习器使用最多的模型是CART决策树和神经网络。
下面看看《机器学习-周志华》8.1节的理论分析。
考虑一个二分类问题\(y \in \{-1, +1\}\),真实函数\(f\)以及奇数\(M\)个犯错概率相互独立且均为\(\epsilon\)的个体学习器(或基学习器)\(h_i\)。我们用简单的投票进行集成学习,即分类结果取半数以上的基学习器的结果:
由Hoeffding不等式知,集成学习后的犯错(即过半数基学习器犯错)概率满足
上式指出,当犯错概率独立的基学习器个数\(M\)很大时,集成后的犯错概率接近0,这也很符合直观想法: 大多数人同时犯错的概率是比较低的。
但是要注意,以上推论全部建立在基学习器犯错相互独立的情况下,而实际中这些学习器不可能相互独立,而如何让基学习器变得“相对独立一些”,也即增加这些基学习器的多样性,正是集成学习需要考虑的主要问题。
根据个体学习器的生成方式,目前的集成学习方法大致可分为两大类,
- 个体学习器间存在强依赖关系、必须串行生成的序列化方法,代表算法是Boosting;
- 个体学习器间不存在强依赖关系、可同时生成的并行化方法,代表算法是Bagging和"随机森林" (Random Forest)。
3. Boosting
Boosting是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值\(T\),最终将这\(T\)个基学习器进行加权结合。Boosting系列算法里最著名算法主要有AdaBoost算法和提升树(boosting tree)系列算法。提升树系列算法里面应用最广泛的是梯度提升树(Gradient Boosting Tree)。
Boosting的原理我们可以用图2概括一下:
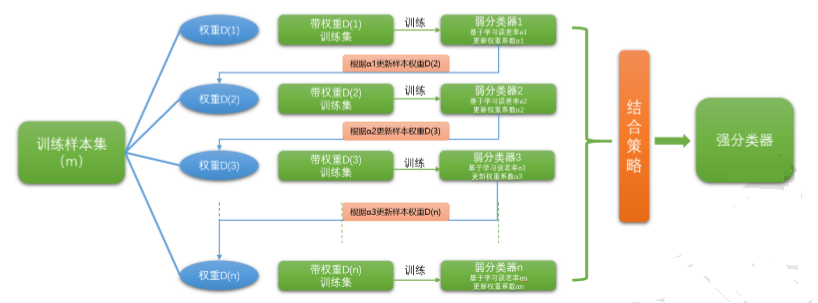
图2 Boosting示意图
弱学习器常指泛化性能略优于随机猜测的学习器,例如在二分类问题上精度略高于50%的分类器。
从偏差-方差分解的角度看,Boosting主要关住降低偏差,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成。
4. Bagging
Bagging的算法原理和 boosting不同,它的弱学习器之间没有依赖关系,可以并行生成,我们可以用图3做一个概括如下:
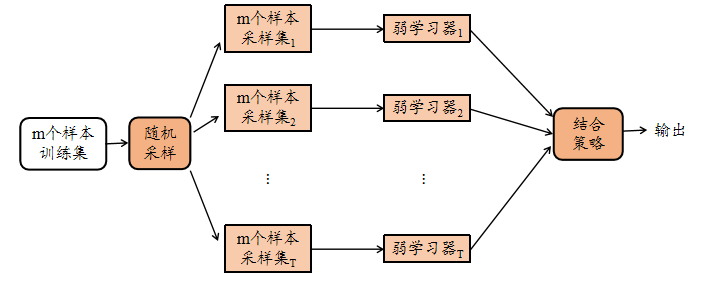
图3 Bagging示意图
Bagging这个名字是由Bootstrap AGGregatlNG缩写而来。从名字即可看出,它直接基于自助采样法 (bootstrap sampling)。给定包含\(m\)个样本的数据集,我们先随机取出一个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中,这样,经过\(m\)次随机采样操作,我们得到含\(m\)个样本的采样集,初始训练集中有的样本在采样集里多次出现,有的则从未出现。照这样,我们可采样出\(T\)个含\(m\)个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些基学习器进行结合。这就是Bagging的基本流程。
对于一个样本,它在某一次含\(m\)个样本的训练集的随机采样中,每次被采集到的概率是\(\frac{1}{m}\)。不被采集到的概率为\(1−\frac{1}{m}\)。如果\(m\)次采样都没有被采集中的概率是\((1−\frac{1}{m})^m\)。当\(m \rightarrow \infty\)时,\((1−\frac{1}{m})^m \rightarrow \frac{1}{e} \approx 0.368\)。也就是说,在Bagging的每轮随机采样中,训练集中大约有63.2%的数据出现在采样集中。这样,由于训练数据不完全相同,我们获得的基学习器可以具有比较大的差异。而且也可以保证每个基学习器有较好的表现。
对于剩余的大约36.8%的没有被采样到的数据,我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合,因此可以用来检测模型的泛化能力。
在对预测输出进行结合时,Bagging通常对分类任务使用简单投票法,对回归任务使用简单平均法。若分类预测时出现两个类收到同样票数的情形,则最简单的做法是随机选择一个,也可进一步考察学习器投票的置信度来确定最终胜者。
从偏差方差分解的角度看, Bagging主要关注降低方差,因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显。
5. 结合策略
在上面几节里面我们主要关注于学习器,提到了学习器的结合策略但没有细说,本节就对集成学习的结合策略做一个总结。我们假定我得到的\(T\)个弱学习器是\(\{h_1,h_2,\dots,h_T\}\)。
5.1 平均法
对于数值类的回归预测问题,通常使用的结合策略是平均法,也就是说,对于若干个弱学习器的输出进行平均得到最终的预测输出。
最简单的平均是算术平均,也就是说最终预测是
如果每个个体学习器有一个权重\(w\),则使用加权平均,最终预测是
其中,\(w_i\)是个体学习器\(h_i\)的权重,通常有
5.2 投票法
对于分类问题的预测,我们通常使用的是投票法。假设我们的预测类别是\(\{c_1,c_2,\dots,c_K\}\),对于任意一个预测样本\(x\),我们的\(T\)个弱学习器的预测结果分别是\((h_1(x),h_2(x),\dots,h_T(x))\)。
最简单的投票法是相对多数投票法,也就是我们常说的少数服从多数,也就是\(T\)个弱学习器对样本\(x\)的预测结果中,数量最多的类别\(c_i\)为最终的分类类别。如果不止一个类别获得最高票,则随机选择一个做最终类别。
稍微复杂的投票法是绝对多数投票法,也就是我们常说的要票过半数。在相对多数投票法的基础上,不光要求获得最高票,还要求票过半数。否则会拒绝预测。
更加复杂的是加权投票法,和加权平均法一样,每个弱学习器的分类票数要乘以一个权重,最终将各个类别的加权票数求和,最大的值对应的类别为最终类别。
5.4 学习法
上两节的方法都是对弱学习器的结果做平均或者投票,相对比较简单,但是可能学习误差较大,于是就有了学习法这种方法,对于学习法,代表方法是stacking,当使用stacking的结合策略时, 我们不是对弱学习器的结果做简单的逻辑处理,而是再加上一层学习器,也就是说,我们将训练集弱学习器的学习结果作为输入,将训练集的输出作为输出,重新训练一个学习器来得到最终结果。
在这种情况下,我们将弱学习器称为初级学习器,将用于结合的学习器称为次级学习器。对于测试集,我们首先用初级学习器预测一次,得到次级学习器的输入样本,再用次级学习器预测一次,得到最终的预测结果。
参考来源:
1)机器学习 - 周志华
2)https://www.cnblogs.com/pinard/p/6131423.html


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号