机器学习笔记-为什么梯度反方向是函数值下降最快的方向

为什么梯度反方向是函数值下降最快的方向？

---

在学习机器学习算法的时候，很多训练算法用的就是梯度下降，然后很多资料也说朝着梯度的反方向变动，函数值下降最快，但是究其原因的时候，很多人都表达不清楚，其中当然包括我了。所以就搬运了几篇博客文章（总有一款适合自己），学习一下为什么梯度反方向是函数值局部下降最快的方向？

第一篇

转载：机器学习--什么是梯度？为什么梯度方向就是函数上升最快的方向？本文将给你解惑

1. 梯度、向量内积、导数与偏导数

什么是梯度？为什么梯度方向就是函数上升最快的方向？又为什么有梯度下降的说法？他们有什么联系？

讲梯度的定义之前，先说明一下梯度它不是一个实数，他是一个向量，即有方向有大小。这个向量有什么特点呢？这里以二元函数为主讲解，先给出公式：

我们在这里说的向量通常是指列向量，下同

设一个多元函数为\(f(x,y)\)，在某点\((x_0,y_0)\)的梯度为这点的偏导，即：

\[\nabla f(x_0,y_0) = (\cfrac{\partial f}{\partial x}, \cfrac{\partial f}{\partial y})^T \]

其中\(\nabla f(x_0,y_0)\)是函数\(f\)在这一点的梯度符号，是一个整体，而\(\cfrac{\partial f}{\partial x}, \cfrac{\partial f}{\partial y}\)是函数\(f(x,y)\)在点\((x_0,y_0)\)处的偏导数。

看到这里大家肯定是晕晕的，别急我们慢慢往下看，现在问题来了，为什么在多元函数中某点的梯度就是该函数在这一点的偏导数呢？为什么不是二阶偏导数不是其他而是一阶偏导数呢？为什么会这样呢？基础不好的同学可能还会问什么是偏导数呢？什么是向量呢？上面这个定义，大家看了下面理解以后再过来看就懂了。

大家还记得什么是向量吗？怎么定义的？

在平面直角坐标系中，分别取与\(x\)轴、\(y\)轴方向相同的两个单位向量\(\pmb i\)，\(\pmb j\)作为一组基底。\(\vec{a}\)为平面直角坐标系内的任意向量，以坐标原点\(O\)为起点作向量\(OP = \vec{a}\)。由平面向量基本定理可知，有且只有一对实数\((x,y)\)，使得向量\(OP = x\pmb i+y\pmb j\)，因此\(\vec{a} = x\pmb i+y\pmb j\)，我们把实数对\((x,y)\)叫做向量的坐标，记作\(\vec{a} = (x,y)\)。显然，其中\((x,y)\)就是点\(P\)的坐标。这就是向量的坐标表示。三维的也是这样表示的。

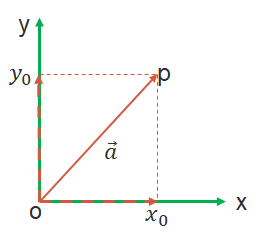
图1 向量的坐标表示

那么这样大家就能理解向量是可以使用坐标表示的，同时解释了\(\nabla f(x_0,y_0)\)是一个向量的表示，虽然没有箭头，但是它也是向量呀，而且就是梯度，现在大家应该可以理解为什么说\(\nabla f(x_0,y_0)\)它是一个向量，到这里我们还需要一点矩阵方面的知识，例如矩阵方面的向量什么？这里的向量和矩阵的向量有所不同，大家需要区别开，因为应用不同，所有定义有点不同，但是具有相同的性质，即有大小有方向。后面会发现就是通过向量把他们的关系建立起来的。

矩阵：矩阵大家都知道，矩阵的向量默认为列向量即一列为一组向量（这点特别重要，大家务必留心，这关系后面的梯度证明的理解），矩阵中的向量有什么性质呢？在这里只提用到的性质，降低难度，即向量的范数（在空间向量中称为模），以及两个向量的內积。

向量的内积：

1）代数定义：

设二维空间内有两个向量\(\vec{a}=(x_1,y_1)\)和\(\vec{b}=(x_2,y_2)\)，定义它们的数量积（又叫内积、点积）为以下实数：

\[\vec{a}\cdot \vec{b} = x_1x_2+y_1y_2 \]

更一般地，\(n\)维向量的内积定义如下:

\[a \cdot b = \sum_{i=1}^na_ib_i=a_1b_1+a_2b_2+\cdots+a_nb_n \]

2）几何定义：

设二维空间内有两个向量\(\vec{a}\)和\(\vec{b}\)，\(|\vec{a}|\)和\(|\vec{b}|\)表示向量\({a}\)和\({b}\)的大小，它们的夹角为\(\theta\)，则内积定义为以下实数：

\[\vec{a}\cdot \vec{b} = |\vec{a}||\vec{b}|cos\theta \]

该定义只对二维和三维空间有效。內积的物理意义就是\(b\)向量在\(a\)向量的投影的乘积或者说\(a\)向量在\(b\)向量投影的乘积，他们是一样的。

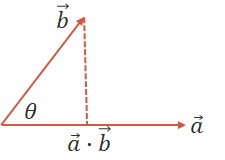
图2 向量的内积

此时大家看到了內积的定义，知道內积计算结果是一个实数，不是向量，既然是一个数那就存在最大值和最小值，再看看这个公式\(|\vec{a}||\vec{b}|cos\theta\)，因为\(cos\theta\)的范围为\([-1,1]\)，所以內积的范围为\([-|ab|,|ab|]\)，因此存在最大值和最小值，当\(\theta\)取180°时最下，当\(\theta\)取0时最大，由此我们可知只要这两个向量共线就会取极值，如果共线同向则取极大值，反之取极小值，所谓共线就是两线平行的意思。这个概念很重要，大家务必理解了，这将直接关系能否理解梯度。下面介绍矩阵这方面内容。

矩阵向量：

\(n\)维向量的内积：设\(n\)为向量

\[x=\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} \quad y = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}\]

称\(x_1y_1+x_2y_2+\cdots+x_ny_n\)为向量\(x\)与\(y\)的内积，记作\([x,y]=x^Ty=x_1y_1+x_2y_2+\cdots+x_ny_n\)。

从这里大家可以看到，矩阵中向量的內积定义和平面向量的定义很像，只是他们的表达不一样罢了，如果把平面中\(a\)向量和\(b\)向量写成列的形式就一样了。只能说平面向量是矩阵向量的一种特殊情况。大家可以这样理解，

\[\vec{a}=\begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \quad \vec{b} = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix}\]

则，\(\vec{a}\cdot \vec{b} = \vec{a}^T\vec{b} = x_1x_2+y_1y_2\)。

因为矩阵向量是列向量，而矩阵的运算法则是行乘以列，因此矩阵向量求內积需要转置一下才能求出是一个数。到这里大家知道了矩阵的向量计算內积公式了，总结一下：

设矩阵向量为\(A\)、\(B\)，则他们的內积为\(A^TB\)，既然是內积，那它也有最大值和最小值，和平面理解一样，两向量同向，值最大，反向值最小（这个概念很重要的，理解透什么是內积，切记矩阵向量內积的形式），这样大家可以理解內积了，至于梯度，大家别急，基础理解了，梯度自然而然的就理解了。下面是导数方面的内容。

什么是导数？什么是偏导数？他们有什么物理意义？梯度和导数、向量有什么关系？

大家都知道导数是代表函数（曲线）的斜率，是描述函数（曲线）变化快慢的量，同时曲线的极大值点也可以使用导数来判断，即极大值点的导数为0，此时斜率为零（现在不深入讨论，后面会通过泰勒级数进行讨论，一阶导数为零的点不一定是极值点可能是驻点，这时需要根据二阶导数判断），那么导数就为我们求解函数的极值提供了可能，当然我们现在说的导数是一元导数，即\(f(x)\)，只具有一个变量，因此很容易求导。

那么什么是偏导数呢？我们知道导数是指一元函数的，它的物理意义就是衡量函数变化快慢的量，例如一天中，温度随时间变化的函数就是一元函数，而多元函数是指形如\(f(x,y)\)、\(f(x,y,z)\)、\(f(x,y,z,w,v)\)等的函数，此时函数的自变量有多个，在这里以二元函数为例说明，我们知道，一旦变量增多，意味着影响因素增加，例如一天的气温不仅和时间有关还是天气有关，还和地理位置有关等，但是我们就想知道，在这多种因素的影响下，哪个因素对它影响最大，怎么办呢？所谓的影响最大就是这个因素对气温的影响最大，即求气温的最值，这时候大家可能会说求导啊，对呀，求导最好了，但是这里有很多变量啊，例如\(f(x,y)\)，我想求\(x\)对\(f\)的影响，怎么办呢？初中我们都学过一个实验方法就是控制变量法，即当我需要改变一个量时，让其他量不变的情况下去改变这个量然后观察对函数的影响，那么我们多元求导可不可以也使用这样的方法呢？当我求\(x\)对\(f\)的影响时，我把\(y\)当做常量来处理，然后对\(x\)求导即可，当然可以啊，只是这时候的求导不在是导数了，因为多元函数是对一个因素也就是\(x\)进行求导，因此称为偏导，这下大家理解为什么有称为偏导了吧。

总结一下：偏导数是指在多元函数的情况下，对其每个变量进行求导，求导时，把其他变量看做常量进行处理，物理意义就是查看这一个变量在其他情况不变的情况下对函数的影响程度。

那什么是梯度呢？和上面又有什么关系呢？

再说梯度之前还是要先说一下泰勒级数，为什么要说这个泰勒级数，因为证明梯度方向总是指向函数最大增加方向的一个关键支撑。

2. 泰勒级数

数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够平滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值，即泰勒级数在某一邻域内去无限接近该函数的一个公式。详解泰勒级数可参考这篇文章

假设有一条解析式很“恶心”的曲线\(f(x)\)，我们可以用多项式仿造一条曲线\(g(x)\)，那么

\[f(x) \approx g(x) = f(x_0) + \cfrac{f^1(x_0)}{1!}(x-x_0)+ \cfrac{f^2(x_0)}{2!}(x-x_0)^2+\cdots+ \cfrac{f^n(x_0)}{n!}(x-x_0)^n \]

泰勒指出：在实际操作过程中，可根据精度的要求选择\(n\)值，只要\(n\)不是正无穷，那么一定要保留上式中的约等号。

这里引入泰勒级数的目的是为了证明极值点的导数问题，高阶函数一般要使用到矩阵论的海森矩阵相关知识，这里不引入那么深的概念，但是基本的矩阵知识还是需要的。

我们只保留前三项：

\[f(x_k+\delta) \approx f(x_k) + f^{'}(x_k)\delta + \cfrac{1}{2}f^{''}(x_k)\delta^2 \]

上面提到了一阶导数是极值点。现在解释为什么会是这样，上面的\(\delta\)是指很小的步长，当\(\delta \gt 0\)时说明\(x\)向右走，当\(\delta \lt 0\)时说明\(x\)向左走，学过高等数学极限的应该有这个概念，现在我们通过泰勒级数只考虑上面公式的前两项来解释为什么，极值点处的一阶导数为0。

\[f(x_k+\delta) \approx f(x_k) + f^{'}(x_k)\delta \]

假如\(x_k\)这一点的函数值\(f(x_k)\)为极值点，可以是极小值或者极大值，这里以极大值点为讲解内容:

因为此时的\(f(x_k)\)为极大值，无论\(\delta \gt 0\)还是\(\delta \lt 0\)，有\(f(x_k+\delta) \lt f(x_k)\)，那么上面的公式想要成立，只能让\(f^{'}(x_k)=0\)才能成立，极小值也是这样证明的，无需画图，从泰勒级数就可以说明极值点的一阶导数一定为0，那么一阶导数为零的点不一定是极值点怎么证明呢？使用三项即可证明，下面证明;

一阶导数为零不一定是极值点：

\[f(x_k+\delta) \approx f(x_k) + f^{'}(x_k)\delta + \cfrac{1}{2}f^{''}(x_k)\delta^2 \]

如果\(f^{'}(x_k)=0\)，那么公式可写成这样：

\[f(x_k+\delta) \approx f(x_k) + \cfrac{1}{2}f^{''}(x_k)\delta^2 \]

从上式可以看到如果在\(f^{'}(x_k)=0\)时假如\(f(x_k)\)为极大值，理应说无论\(\delta \gt 0\)还是\(\delta \lt 0\)，有\(f(x_k+\delta) \lt f(x_k)\)，但是此时如果\(f^{''}(x_k) \gt 0\)，则\(f^{''}(x_k)\delta^2 \ge 0\),所以\(f(x_k+\delta) \gt f(x_k)\)，即证得\(f(x_k)\)不是极大值点，那如何才能判断是极值点呢？

此时需要借助二阶导数，上面如果\(f^{''}(x_k) \lt 0\)则为极大值点，所以才有一阶导数等于零，二阶导数小于零为极大值点，如果二阶导数大于零则为极小值点。如果二阶导数等于0怎么办？那就继续判断三阶导数就可以了。

这是在标量的情况下的极值问题，如果\(x\)是向量怎么处理呢？

还是引入泰勒公式就可以了。只是不一样的是都是向量了：

我们知道机器学习中的变量都很多，一般都使用向量进行表示（此时为列向量）且为多元函数，求导和标量一样的，只是现在是求偏导了。

\[f(X_k+\delta) \approx f(X_k) + f^{'}(X_k)^T\delta + \cfrac{1}{2}f^{''}(X_k)^T\delta^2 \]

公式中\(f(X_k),f^{'}(X_k),f^{''}(X_k),\delta\)都是向量，例如一阶偏导\(f^{'}(X_k)\)应该是这样的：

\[\cfrac{\partial f(X)}{\partial X} = \begin{bmatrix} \cfrac{\partial f(X)}{\partial x_1} \\ \vdots \\ \cfrac{\partial f(X)}{\partial x_n} \end{bmatrix}\]

因为是向量，所以有大小有方向了，大家注意到了没有，此时的\(f^{'}(X_k)^{T}\)为行向量了，因为转置了，因此和\(\delta\)相乘是內积，此时我们也只看前两项即：

\[f(X_k+\delta) \approx f(X_k) + f^{'}(X_k)^T\delta \]

现在重点来了啊，为了每次\(x\)前进的方向是使函数\(f(X_k)\)增长最快，应该怎样选取前进方向的步伐\(\delta\)（向量），才能保证呢？好，大家能看到\(\delta\)直接影响着\(f^{'}(X_k)^T\delta\)，而决定\(f(X_k+\delta)\)的值是由\(f(X_k)\)、\(f^{'}(X_k)^T\delta\)决定，然而\(f(X_k)\)是确定的，所以使其\(f^{'}(X_k)^T\delta\)最大即可，而该式就是向量的內积，根据上面讲了半天的向量內积可知，只要使\(\delta\)取的向量和\(f^{'}(X_k)\)共线就可以了，如果共线同向则取最大方向，反向取最小小方向。因此直接使\(\delta\)=\(f^{'}(X_k)\)即可，即保证方向共线就可以了，至于值得大小可以乘一个标量，现在我们找到了这个向量，而这个向量就是多元函数的一阶偏导数，这时候就定义，多元函数的一阶偏导数为梯度，符号为\(\nabla f(x_0,y_0)\)，数学上的梯度就是这么来的，此时就可以写成这样了：

\[f(X_k+\delta) \approx f(X_k) + \nabla^Tf(X_k)\delta + \cfrac{1}{2}\delta^T\nabla^2f(X_k)\delta^2 \]

好，到这里我们知道了什么是梯度，梯度怎么来的，总结来说梯度是为了寻找极值而生的，而且是极大值，因此梯度总是指向函数增长最快的方向，这就是本质原因了，但是我们常听的是梯度下降，改变梯度方向就是下降最快的，共线反向取极小值就是这个道理了。

该式更能反映事实。大家细细品味，梯度的知识点难在理解上，梯度不是标量，他是向量，有方向有大小，一般我们不是很关心大小，因为可以通过标量放大或者缩小，重要的是方向问题，因为只要确定增长最快的方向，才能找到极值点，这也是很多算法使用梯度优化算法的原因，当然是梯度的反方向，

到现在基本上就结束了，但是我还是有些知识需要交代，矩阵方面的没给大家深入讲，可能上面的证明还是不够严谨，但是证明思路已经出来了，理解梯度已经够用了，如果感兴趣，建议大家有时间看看张贤达的矩阵论，里面有更严谨的数学推到，在这里希望给大家一种抛砖引玉的感觉，矩阵论对这方面讲解的很透彻，主要牵扯到二次型、正定、半正定等知识。有时候感觉数学没什么用，其实用处很大的，需要我们学习者内化或者理解其物理意义，搞明白来龙去脉，方能正确使用数学这把利剑，梯度到此结束，有问题欢迎交流。

第二篇

转载：在梯度下降法中，为什么梯度的负方向是函数下降最快的方向？

1. 概念引入

需要了解的数学知识有导数，偏导数(这里就不展开了）。

我们引入梯度的概念。假设定义空间是\(n\)维的，我们现在有一个从这个\(n\)维空间映射到\(p\)维空间的函数:

\[\vec{p} =f(\vec{x}) \]

需要注意的是，这里的\(\vec{p}\)是\(p\)维的，\(\vec{x}\)是\(n\)维的。我们设

\[\vec{x} =(x_1,x_2,\dots,x_n) \]

梯度实质上是一个\(n\)维的向量（和\(x\)的维度相同），梯度的每一个维度又是什么呢？梯度的每一个维度是该函数关于这个维度的偏导数。我们将梯度记为\(\vec grad_f\)，将上面这段话公式化就是：

\[\vec grad_f = (\cfrac{\partial f}{\partial x_1}, \cfrac{\partial f}{\partial x_2}, \cdots, \cfrac{\partial f}{\partial x_1}) \]

举一个例子，假设：

\[f(x,y)=(x−2)^2+(y+3)^2 \]

这是一种比较特殊的情况，在这种情况下，我们有\(n=2\)，\(p=1\)。那么怎么计算梯度呢？我们需要根据自变量的每一维度分别计算函数的偏导数，然后把他们组成一个向量就好了。

\[\cfrac{\partial f}{\partial x}=2 \times (x−2) \]

\[\cfrac{\partial f}{\partial y}=2\times (y+3) \]

因此，这个函数的梯度就是

\[\vec grad_f = (2x-4, 2y+6) \]

然后，对于每一个给定的\((x，y)\)我们都可以求出函数在这个点的梯度的数值（带入就可以了）。

2.证明

接下来，我们来证明我们的目标：为什么上面定义的梯度是函数在该点上升最快的方向呢？换句话讲，就是为什么函数在该点下降最快的方向是梯度的负方向呢？现在，让我们假设一个下降的方向，这个方向是随机的，我们设这个方向是

\[\vec{l} =(l_1,l_2,...,l_n) \]

什么意思呢？就是说我们现在处于函数的一个点上，这个点的坐标是

\[\vec{x} =(x_1,x_2,\dots,x_n) \]

我们在这点的函数值是

\[f(\vec{x}) \]

我们想要去到这个函数更低的地方去，这个低在数学上的体现就是函数值变小。在机器学习当中，就是我们的误差函数变小。那么我们沿着\(\vec{l}\)下降的意思就是，我们下一步将来到

\[f(\vec{x}+\vec{l}) \]

当然，由于我们的\(\vec{l}\)方向是完全随机的，所以实际上我们并不能得知函数值到底是增大还是减小，然而这并不影响我们的证明。

根据多元函数的一阶泰勒展开公式，我们有：

\[f(\vec{x}+\vec{l})=f(\vec{x})+\sum_{k=1}^n\cfrac{\partial f}{x_k}\times l_k+o(||x||^n) \]

这个公式的证明就不在这里展开了。

我们发现，

\[f(\vec{x}+\vec{l}) - f(\vec{x}) \]

就是我们沿着\(\vec{l}\)方向移动前后，函数值的变化量。也就是说，只要这个值小于零，我们的函数值就在变小;而只要我们可以证明当\(\vec{l}\)取到梯度的负方向时这个值小于零且绝对值最大，那么我们就证明了我们的目标。而我们知道，这个值等于（就是移项）

\[\sum_{k=1}^n\cfrac{\partial f}{x_k}\times l_k+o(||x||^n) \]

又因为，当我们的自变量变化值极小的时候(\(||\vec{l}||\)极小)，我们是可以忽略

\[o(||x||^n) \]

这一项的。在机器学习当中，这个条件很容易被满足，因为只要我们取得的学习速率\(\alpha\)很小的时候，我们可以近似认为这个条件已经被满足。因此，我们现在仅剩的问题就是如何找到一个方向，使得

\[\sum_{k=1}^n\cfrac{\partial f}{x_k}\times l_k \]

小于零且绝对值最大。我们观察这一项可以发现，它其实是两个向量的数量积（scalar product），也就是

\[\langle \vec grad_f , \vec{l}\rangle \]

(这个表示\(\vec grad_f\)和\(\vec{l}\)的数量积）

根据柯西-施瓦兹不等式，我们可以得知当且仅当这两个向量方向相同时，该数量积的绝对值取得最大值。注意，这里只是绝对值最大。我们已经胜利了一半，而最后一个小于零的条件很容易满足，我们只需要让

\[\vec{l} = -\vec grad_f \]

这样的话，对于这两个向量来说，他们的每一个维度都互为对方的相反数，因此他们的数量积一定不可能大于零，在实际情况下，他们甚至一直小于零，到这里，我们就证明了当且仅当\(\vec{l}\)的方向是负梯度方向时，函数值下降最快。

第三篇

转载：证明：梯度方向是变化最快的方向

首先，回顾我们怎么在代码中求梯度的（梯度的数值定义）

1）对向量的梯度

以\(n\times 1\)实向量\(x\)为变元的实标量函数\(f(x)\)相对于\(x\)的梯度为一\(n\times 1\)列向量\(x\)，定义为

\[\nabla_{\boldsymbol{x}} f(\boldsymbol{x})\overset{\underset{\mathrm{def}}{}}{=} \left[ \frac{\partial f(\boldsymbol{x})}{\partial x_1}, \frac{\partial f(\boldsymbol{x})}{\partial x_2},\cdots,\frac{\partial f(\boldsymbol{x})}{\partial x_n} \right]^T=\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}} \]

2）对矩阵的梯度

实标量函数\(f(A)\)​相对于\(m×n\)实矩阵\(A\)的梯度为一\(m×n\)矩阵，简称梯度矩阵，定义为

\[\nabla_{\boldsymbol{A}} \boldsymbol f(\boldsymbol{A})\overset{\underset{\mathrm{def}}{}}{=} \begin{bmatrix} \frac{\partial f(\boldsymbol{A})}{\partial a_{11}} &\frac{\partial f(\boldsymbol{A})}{\partial a_{12}} & \cdots & \frac{\partial f(\boldsymbol{A})}{\partial a_{1n}} \\ \frac{\partial f(\boldsymbol{A})}{\partial a_{21}} &\frac{\partial f(\boldsymbol{A})}{\partial a_{22}} & \cdots & \frac{\partial f(\boldsymbol{A})}{\partial a_{2n}} \\ \vdots &\vdots & \ddots & \vdots \\ \frac{\partial f(\boldsymbol{A})}{\partial a_{m1}} &\frac{\partial f(\boldsymbol{A})}{\partial a_{m2}} & \cdots &\frac{\partial f(\boldsymbol{A})}{\partial a_{mn}} \\ \end{bmatrix}=\frac{\partial \boldsymbol{f}(\boldsymbol{A})}{\partial \boldsymbol{A}} \]

然后我们回顾一下导数和方向导数：

1）导数和偏导

导数是函数在某一点的变化率，在一元函数中，就是沿着x轴在某一点的变化率；在二元函数中，就有了偏导，在x方向上的偏导，就是函数在某一点沿着x轴方向的变化率，在y方向上的偏导同理；在更多元函数中以此类推。

2）方向导数

上一点只涉及到坐标轴方向的变化率，那如果我想要知道任意方向的变化率呢？这就引出了方向导数的概念，方向导数是偏导数的概念的推广。

现在我们回到梯度：

梯度方向就是方向导数值最大的那个方向，那根据上面梯度的数值定义，“为什么梯度方向是变化最快的方向”这个问题就等价于“为什么多元函数各个轴方向的变化率（这里指向量）的合方向就是整个函数值变化率最大的方向？”

以二元函数为例：

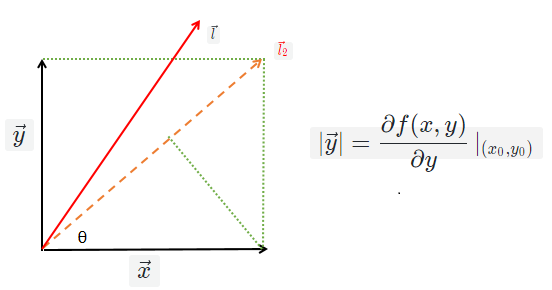
已知：\(\vec{x},\vec{y}\)分别是二元函数\(f(x,y)\)在点\((x_0,y_0)\)处沿\(x,y\)轴的偏导数，\(\vec{l}\)是任意方向的方向导数。

求证：\(\vec{l}_2\)的方向是二元函数\(f(x,y)\)在点\((x0,y0)\)处变化最快的方向。

证明：

函数\(f(x,y)​\)在点\((x_0,y_0)\)​处沿方向\(\vec{l}\)的变化率为\(|\vec{l}|=|\vec{x}|cos\theta+|\vec{y}|sin\theta\)​，则

\(|\vec{l}|​\)最大等价于点\((|\vec{x}|,|\vec{y}|)\)​与点\((cos\theta,sin\theta)​\)的内积最大（内积的坐标定义），

将上面的内积化为向量形式：记\(\vec{A} =(|\vec{x}|,|\vec{y}|),\vec{B}=(cos\theta,sin\theta)​\)，则\(\vec{A} \cdot \vec{B}=|\vec{A}| \cdot |\vec{B}|\cdot cos\alpha​​\)，其中\(\alpha\)​是\(\vec{A} ,\vec{B}\)的夹角；

则\(|\vec{l}|​\)最大等价于\(\vec{A} \cdot \vec{B}\)​最大，在问题的设定下\(\theta\)​是变量，于是等价于\(\vec{A} ,\vec{B}\)方向平行，而\(\vec{A}\)的方向就是\(\vec{l}_2\)的方向，故\(\vec{B}\)的方向取\(\vec{l}_2\)的方向时，取到最大变化率。

于是由梯度的数值化定义出发，可以证明梯度方向就是方向导数值最大的那个方向，这个方向就是\(\vec{A}\)的方向（注意看它的坐标）。

以上都是在二元函数的情况下进行证明的，同理可以证明多元函数的情况：

比如三元函数\(f(x,y,z)\)，沿\(\vec{l}\)方向的方向导数的大小为\(|\vec{l}|=|\vec{x}|cos\theta_1+|\vec{y}|cos\theta_2+|\vec{z}|cos\theta_3\) (1)，其中\(\theta_1,\theta_2,\theta_3\)分别是\(x,y,z\)轴和任意方向向量\(\vec{l}\)的夹角；于是又可以\(|\vec{l}|=\vec{A} \cdot \vec{B}\)，其中\(\vec{A}=(|\vec{x}|, |\vec{y}|,|\vec{z}|),\vec{B}=(cos\theta_1,cos\theta_2,cos\theta_3)\)，接下来就是同理可证了。

因为(1)处用的是几何观点，更多元的情况从几何角度就想象不出来了，但讲道理是一样的，于是证明结束。