机器学习笔记-梯度下降法

梯度下降法

---

给定数据集\(D=\{(x_i,y_1),(x_2,y_2),\dots,(x_m,y_m)\}\)，其中\(x\)表示特征向量，\(x_i \in R^d\)，\(y\)表示标签，是一个标量，\(y_i \in R\)。在机器学习问题中，我们希望学得一个模型\(f\)来描述输入与输出之间的关系\(f(x_i)\rightarrow y_i\)。

首先我们从简单的问题开始，假设这个模型就是线性模型。那么，什么是线性模型？

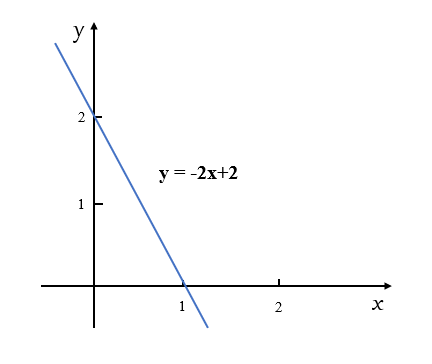
图 1：简单的线性函数

如图1所示，我们知道由图中的两个点\((0,2)\)和\((1,0)\)就可以确定蓝色的这条直线方程，即\(y=-2x + 2\)。

这是一个我们很熟悉的线性函数，其中有两个关键的参数\(-2\)和\(2\)。如果我们用\(\theta_1\)和\(\theta_0\)来分别表示参数\(-2\)和\(2\)，那么，直线方程就可以写成

\[y=\theta_1 x + \theta_0 \tag{1} \]

这是我们熟悉的直线方程\(y=ax+b\)的形式，只是换了一个符号而已。

实际上，我们还可以把这个方程写的更广泛一些，这里要引入一个变量\(x_0\)，且定义\(x_0\)恒等于\(1\)。则式\((1)\)可以写成

\[y=\theta_1x + \theta_0x_0 \tag{2} \]

于是，我们可以用向量的形式表示\(\theta\)和\(x\)，即

\[\theta^T=(\theta_0, \theta_1) \qquad x=\begin{pmatrix} x_0 \\ x_1 \end{pmatrix}\]

因此，线性函数就可以表示成

\[y=\theta_1x + \theta_0x_0 = \theta^Tx\tag{3} \]

更进一步，可以将\(x\)扩展到\(d+1\)为，即\(x \in R^{d+1}\)，\(\theta \in R^{d+1}\)，则

\[y = \theta_0x_0 + \theta_1x_1+,\cdots, \theta_dx_d = \sum_{d=0}^d\theta_dx_d= \theta^Tx \tag{4} \]

此时，如果我们要预测变量\(y_i\)，则根据式\((4)\)，有

\[y_i \approx h_\theta(x_i) = \theta_0x_0 + \theta_1x_{i1}+,\cdots, \theta_dx_{id} = \sum_{d=0}^d\theta_dx_{id}= \theta^Tx_i \]

式\((4)\)看上去好像比较复杂，接下来，我们使用一个最简单的例子，考虑一下，如果将式\((2)\)的\(\theta_0\)置为\(0\)，这样的直线经过坐标原点，没有截距项，这样我们得到了最简单的线性方程，因为此时方程只有一个参数，我们忽略下标，即有

\[h_\theta(x) = \theta x \tag{5} \]

根据式\((5)\)，这样的线性方程如图2所示，如果不断的调整\(\theta\)的值，就得到了经过原点的不同的直线，如图2中的两条直线，\(\theta\)分别等于\(1\)和\(\frac{1}{2}\)。

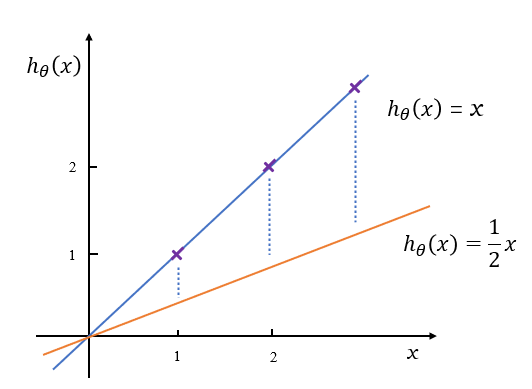
图 2：线性函数的参数

如果\(\theta_0\)不等于0，那么这条直线将不经过坐标原点。

至此，我们知道了什么是线性模型。而在机器学习问题中，通常是给定训练数据，即\(x\)已知，然后求\(\theta\)，使得由该\(\theta\)构成的方程能够尽量好的拟合训练数据，也就是说尽量好的描述输入与输出之间的映射关系。那么，怎么求得最好的\(\theta\)呢？

同样的，我们使用上边的例子，假设给定训练数据集\(D=\{(1,1),(2,2),(3,3)\}\)，将这3个数据点画出来如图2中的紫色点。

现在要学得一个直线\(h_\theta(x)=\theta x\)来拟合这组数据。我们要知道，在给定这样一组数据的条件下，估计出来什么样的\(\hat{\theta}\)能够很好的进行拟合？

根据\(h_\theta(x)=\theta x\)直线方程的特点，它是通过原点的。那么，我们可以假设这条直线是\(h_\theta(x)=\cfrac{1}{2} x\)，如图2中的黄色直线。注意，这是我们的假设。当我们假设数据是由这条直线生成的时候，会发现给定数据和这条线并不拟合，它们之间有很明显的误差，显然，我们要减小这些误差。

于是我们要尝试调整假设的直线的位置，即调整\(\theta\)的值。比如，当\(\theta = 0\)时，直线与\(x\)轴重合，但是会发现误差比黄色直线还要大。需要继续调整，当\(\theta = 1\)的时候，发现3个数据点基本在蓝色的直线上，误差很小，它可能就是我们需要找到的那条直线。

综上，我们要做的就是不断的调整这条线，调整不同的\(\theta\)值，使得数据点到这条直线的距离最短，这样就可以使这条直线能够尽量好的解释这些数据。当然，现实情况中数据点不可能全部恰好通过这条直线，我们只是描述了一个最简单的情况。

前面已经说过，一般来讲，我们希望数据点到假设直线的距离最短，观察发现这些点有的在直线的上面，有的在直线的下面，所以，计算距离时通常用绝对值或者平方项。

接下来，我们就构造一个损失函数\(J(\theta)\)，目的是当我们不断调整假设函数（比如前面描述的调整直线方程）的时候，每调整一次假设函数的参数，希望能够使损失函数的值越来越小。这样我们就知道怎么调整\(\theta\)，也就是说需要给\(\theta\)设定一个目标，显然这个目标一定是关于\(\theta\)的。我们想知道什么样的\(\theta\)最好，当使\(J(\theta)\)最小的时候，就是我们希望找到的\(\theta\)值。对待上述问题时，我们就可以构造下面这样的损失函数

\[J(\theta)= \cfrac{1}{2m}\sum_{i=1}^m(h_\theta(x_i) - y_i)^2 \tag{6} \]

其中，\(h_\theta(x_i)\)是估计值，\(y_i\)是真实值，它们之间的差表示估计误差，如图2中蓝色虚线所示。式\((6)\)表示误差平方和的平均值。而\(\frac{1}{2}\)只是为了方便计算人为加入的，并不会对最终结果产生影响，因为我们只关心\(\theta\)取什么值时\(J(\theta)\)最小，而不关心\(J(\theta)\)的最小值是多少。注意，\(J(\theta)\)是一个关于\(\theta\)的函数。

那么我们就来看一下刚才的例子，在给定数据集\(D=\{(1,1),(2,2),(3,3)\}\)条件下，当我们不断调整\(\theta\)的值时，有

\[J(\theta) = J(0) = \cfrac{1}{2\times 3}((-1)^2+(-2)^2+(-3)^2) = \cfrac{7}{3} \]

\[J(\theta) = J(\cfrac{1}{2}) =\cfrac{1}{2\times 3}((-\cfrac{1}{2})^2+(-1)^2+(-\cfrac{3}{2})^2) = \cfrac{7}{12} \]

\[J(\theta) = J(1) = \cfrac{1}{2\times 3}((0)^2+(0)^2+(0)^2) = 0 \]

描述这个过程是想强调，这个过程的函数关系是关于\(\theta\)的。在整个的假设函数空间中调整\(\theta\)，我们会得到不同的假设函数，且会得到不同的损失函数\(J(\theta)\)的值，我们希望调整\(\theta\)的过程中，使\(J(\theta)\)最小。将过程大概画出来如图3所示

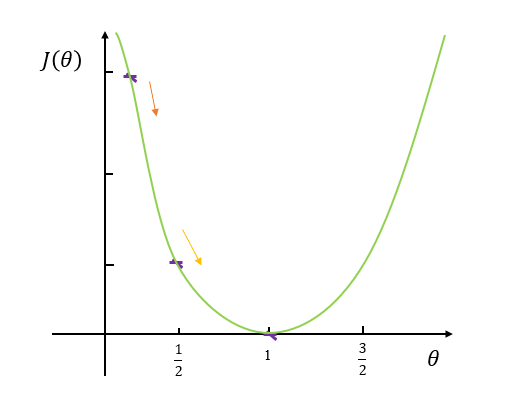
图 3：参数值与损失函数

通过\(\theta\)的不断调整，损失函数值不断的变化，如图3，损失函数有最小值，而使\(J(\theta)\)取得这个最小值时的\(\theta\)就是我们希望找到的最好的\(\theta\)。如上面的例子中，当\(\theta = 1\)时，\(J(\theta)\)最小。

那么，我们通过什么方法不断地调整\(\theta\)呢？例子中只是我们随意选择的值，实际上是有具体的算法来完成这一个过程的，通过随机给定的一个\(\theta\)值，通过算法不断的调整\(\theta\)值，最终达到\(J(\theta)\)最小，这就是我们要描述的梯度下降算法(Gradient decent)。

我们最终的目的是想求损失函数\(J(\theta)\)关于\(\theta\)的最优值，比如，损失函数是上述式\((6)\)，我们想知道怎么调整\(\theta\)的情况下，能够使它最小，即

\[\smash{\min_\theta} J(\theta) = \cfrac{1}{2m}\sum_{i=1}^m(h_\theta(x_i) - y_i)^2 \tag{7} \]

我们知道，从解方程的角度看，我们可以通过求导数达到目的。

而梯度下降法也是基于函数导数的一种方法，其表达式为：

\[\theta_{t+1} \leftarrow \theta_t - \alpha \cfrac{\partial J(\theta)}{\partial \theta_t} \tag{8} \]

其中，\(\theta_t\)表示当前时刻的参数值，\(\theta_{t+1}\)表示下一时刻，即即将更新的参数值，\(\cfrac{\partial J(\theta)}{\partial \theta_t}\)表示当前位置的梯度。\(\alpha(\alpha \ge 0)\)是学习速率(learning rate)，即下降的步长，\(\theta\)更新的速度。

那么，这样一个算法就可以解决刚才的问题吗？是的。

我们来看一下为什么。我们的目的是使\(J(\theta)\)比较小，如图4所示，我们通过不断的调整\(\theta\)找到\(J(\theta)\)的最小值。在梯度下降法中，初始的\(\theta\)值是人为随机指定的，假设就是图4中\(\theta_t\)的位置，令其为\(\theta_0\)，表示\(t=0\)时刻的\(\theta\)值。

接下来，我们要求\(J(\theta)\)对\(\theta_0\)的偏导\(\cfrac{\partial J(\theta)}{\partial \theta_0}\)，我们知道，此时求\(\theta_0\)处的导数就是求函数在该点处的切线，即图中的的红色直线所示，显然此时的得到的偏导数是一个大于0的数，即\(\cfrac{\partial J(\theta)}{\partial \theta_0} \gt 0\)。

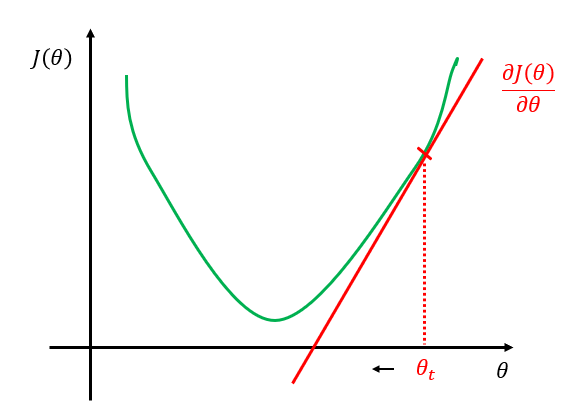
图 4：梯度下降

根据式\((8)\)的参数\(\theta\)的更新规则，我们有

\[\theta_1 \leftarrow \theta_0 - \alpha \cfrac{\partial J(\theta)}{\partial \theta_0} \]

其中，\(\alpha \ge 0\)当\(\alpha=0\)时其实没意义，所以\(\alpha\)通常是大于0的数，而此时\(\cfrac{\partial J(\theta)}{\partial \theta_0}\)也大于0，\(\theta_1\)等于\(\theta_0\)减去一个正数，于是在这种情况下，更新后的\(\theta_1\)相对\(\theta_0\)向左移动，如图4所示。

当初始指定的\(\theta_0\)在另一个点时，如图5所示

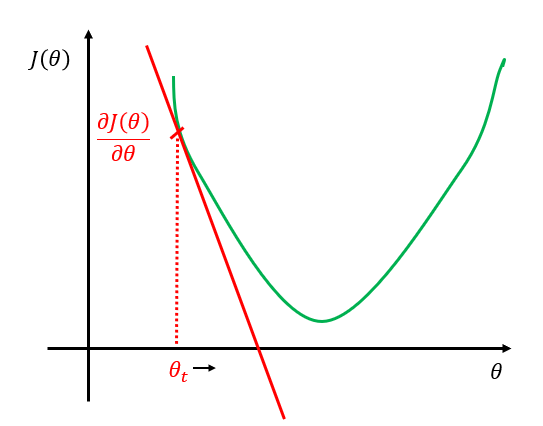
图 5：梯度下降

我们计算得到的\(\cfrac{\partial J(\theta)}{\partial \theta_0}\)小于0，根据式\((8)\)的参数\(\theta\)的更新规则，在这种情况下，更新后的\(\theta_1\)相对\(\theta_0\)向右移动。

我们通过不断的重复上述的过程，导数会逐渐变小，直至趋近于零，此时，就得到了使\(J(\theta)\)最小的\(\theta\)值，这里记作\(\hat \theta\)。梯度下降法就是这样的一个迭代更新参数\(\theta\)的过程，如图6所示。

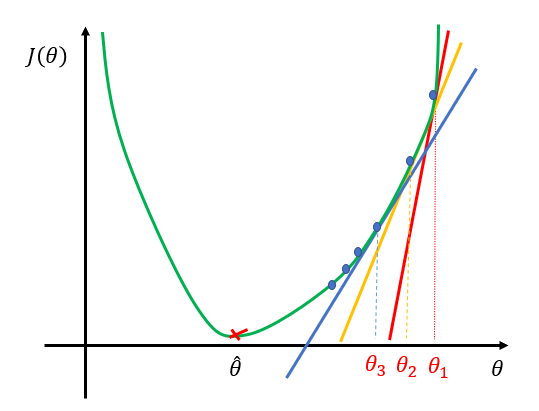
图 6：梯度下降迭代更新参数

这里的\(\hat \theta\)就是我们希望得到的模型的参数

但是，上述情况是比较理想的情况，实际上的梯度下降更复杂。

1）学习速率\(\alpha\)的取值

梯度下降法中的\(\alpha\)前面我们只说它是大于零的数，但是这个取值范围很广，比如可以取0.01，0.0001，100，10000或者其他什么值。那么这个\(\alpha\)怎么取值也是一个很重要的问题。

我们可能会发现这样一个现象，当选择了一个\(\alpha\)值后，我们调整\(\theta\)时，损失函数的值并没有向最优值的方向趋近，而是如图7所示，一直在比较剧烈的波动，这种情况可能是由于\(\alpha\)取值过大。此时，可能需要更多的迭代次数才能达到最优值，甚至无法得到最优值。

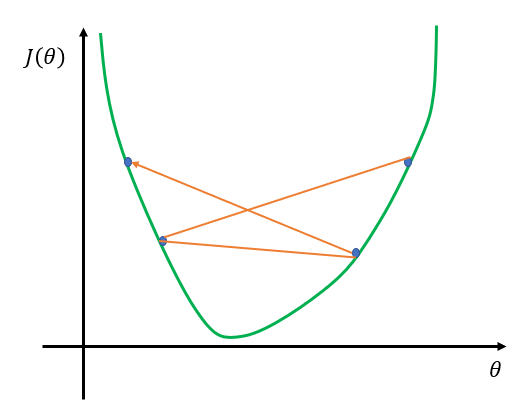
图 7：学习速率取值较大

当然，另一种情况就是\(\alpha\)取值过小，如图8所示，这种情况下，下降过程缓慢，需要非常多的迭代次数才能达到最优值。

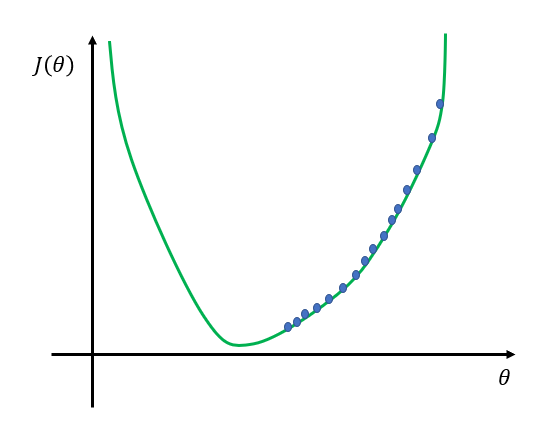
图 8：学习速率取值较小

2）高维情况

前面提到的模型是\(h_\theta(x)=\theta x\)，显然现实问题肯定比这个要复杂，假设我们现在考虑二维的情况，即\(h_\theta(x)=\theta_1 x_1 + \theta_0\)，那么\(J(\theta)\)可以表示为\(J(\theta_0,\theta_1)\)，图像如图9所示

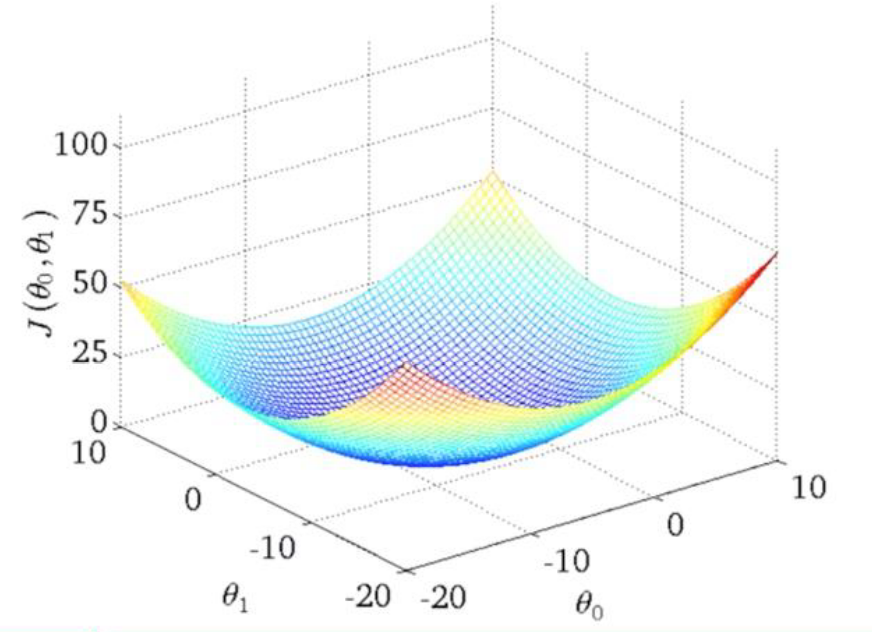
图 9：高维度的梯度下降

此时，要求得\(J(\theta_0,\theta_1)\)最小值点，则参数\(\theta\)的更新规则为

\[\theta_j \leftarrow \theta_j - \alpha \cfrac{\partial J(\theta_1, \theta_0)}{\partial \theta_j}, j=0,1 \tag{9} \]

展开写成

\[\theta_0 \leftarrow \theta_0 - \alpha \cfrac{\partial J(\theta_1, \theta_0)}{\partial \theta_0} \tag{10} \]

\[\theta_1 \leftarrow \theta_1 - \alpha \cfrac{\partial J(\theta_1, \theta_0)}{\partial \theta_1} \tag{11} \]

也就是说，在二维的情况，参数\(\theta\)按照式\((10)\)和\((11)\)在每个维度上进行更新，更高维度以此类推。

我们画一个等高线图来看一下，在二维情况下，梯度的下降方式，如图10所示

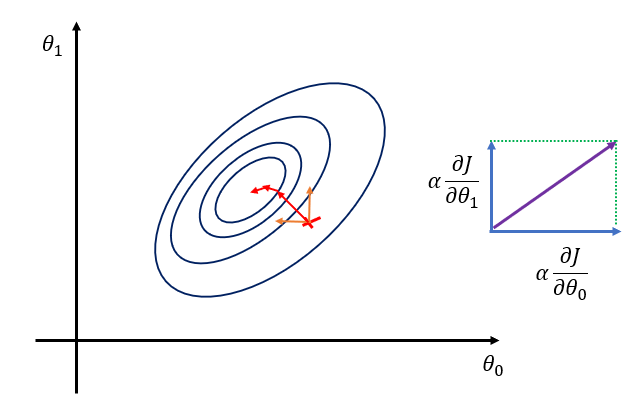
图 10：二维情况下的梯度下降

在具体的问题中，我们需要将梯度计算出来，进而得到\(\theta\)的更新，假设我们的损失函数是前面的\((7)\)，\(h_\theta(x)=\theta_1 x_1 + \theta_0\)，则

\[\begin{aligned} \cfrac{\partial J(\theta_1, \theta_0)}{\partial \theta_0} &= \cfrac{\partial}{\partial \theta_0}(\cfrac{1}{2m}\sum_{i=1}^m(h_\theta(x_i) - y_i)^2) \\ &= \cfrac{1}{m}\sum_{i=1}^m(h_\theta(x_i) - y_i) \end{aligned}\]

\[\begin{aligned} \cfrac{\partial J(\theta_1, \theta_0)}{\partial \theta_1} &= \cfrac{\partial}{\partial \theta_0}(\cfrac{1}{2m}\sum_{i=1}^m(h_\theta(x_i) - y_i)^2) \\ &= \cfrac{1}{m}\sum_{i=1}^m(h_\theta(x_i) - y_i)x_{1i} \end{aligned}\]

注意：\(\theta_0,\theta_1\)需要同时更新，即更新\(\theta_1\)时要使用当前的\(\theta_0\)而不是已经更新后的\(\theta_0\)，反之亦然。

推广到更一般的情况下，仍然以线性模型为例，即\(h_\theta(x) = \sum_{d=0}^d\theta_dx_{id}= \theta^Tx\)。

此时梯度下降法过程为：

1. 初始指定\(\theta^T_0, \theta \in R^{d+1}\)
2. 计算损失函数在各各维度的偏导数\(\cfrac{\partial J(\theta_0, \theta_1,\dots,\theta_d)}{\partial \theta_j}, j=0,1,\dots,d\)
3. 更新参数\(\theta_j\)

仍然以损失函数式\((7)\)为例，则

\[\begin{aligned} \theta_j &\leftarrow \theta_j - \alpha \cfrac{\partial J(\theta_0, \theta_1,\dots,\theta_d)}{\partial \theta_j} \\ &= \theta_j - \alpha \cfrac{\partial}{\partial \theta_0}(\cfrac{1}{2m}\sum_{i=1}^m(h_\theta(x_i) - y_i)^2) \\ &= \alpha \cfrac{1}{m}\sum_{i=1}^m(h_\theta(x_i) - y_i)x_{ji} \end{aligned}\]

注意\(\theta_0\)，因为我们定义\(x_0=1\)，所以

\[\begin{aligned} \theta_0 &\leftarrow \theta_0 - \alpha \cfrac{\partial J(\theta_0, \theta_1,\dots,\theta_d)}{\partial \theta_j} \\ &= \theta_0 - \alpha \cfrac{\partial}{\partial \theta_0}(\cfrac{1}{2m}\sum_{i=1}^m(h_\theta(x_i) - y_i)^2) \\ &= \alpha \cfrac{1}{m}\sum_{i=1}^m(h_\theta(x_i) - y_i) \end{aligned}\]

4. 迭代步骤2和3，直至\(\theta\)不在变化或变化小于某阈值

3）局部最优与全局最优

梯度下降算法不能保证找到的是全局最优点，可能会陷入局部最优，如图11所示。

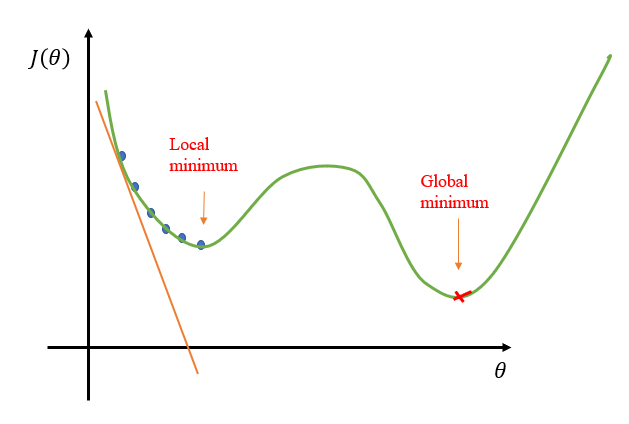
图 11：局部最优与全局最优

有一些方法可以解决这一问题，本篇笔记不再展开。

梯度下降数学原理

对于梯度下降算法（Gradient Descent Algorithm），我们都已经很熟悉了。无论是在线性回归（Linear Regression）、逻辑回归（Logistic Regression）还是神经网络（Neural Network）等等，都会用到梯度下降算法。

首先理解什么是梯度？通俗来说，梯度就是表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在当前位置的导数。

\[\nabla = \cfrac{df(\theta)}{d\theta} \]

上式中，\(\theta\)是自变量，\(f(\theta)\)是关于\(\theta\)的函数，\(\nabla\)表示梯度。

梯度下降算法的公式我们在上面已经提过了，即

\[\theta = \theta_0 - \eta \cdot \nabla f(\theta_0) \]

其中，\(\theta_0\)是自变量参数，表示当前位置坐标，\(\eta\)是学习速率，即每次前进的步长，\(\theta\)是更新后的\(\theta_0\)，即移动一小步后的位置坐标。（为了方便，公式与之前的描述做了一些符号上的改变，其实是一样的）

接下来，我们来看一下梯度下降算法是如何推导的。

这里需要一些预备知识，即泰勒展开式，这里不再对其进行详细说明，我们直接使用一阶泰勒展开式，如下：

\[f(\theta) \approx f(\theta_0) + (\theta - \theta_0) \cdot \nabla f(\theta_0) \]

其中，\(\theta - \theta_0\)是微小矢量，它的大小就是我们之前讲的步进长度\(\eta\)，注意它是一个标量，用\(v\)表示\(\theta - \theta_0\)的单位向量，则可以将\(\theta - \theta_0\)表示为

\[\theta - \theta_0 = \eta v \]

特别需要注意的是，\(\theta - \theta_0\)不能太大，因为太大的话，泰勒展开式的线性近似就不够准确，一阶泰勒近似也不成立了。替换之后，\(f(\theta)\)的表达式为：

\[f(\theta) \approx f(\theta_0) + \eta v \cdot \nabla f(\theta_0) \]

重点来了，局部下降的目的是希望每次\(\theta\)更新，都能让函数值\(f(\theta)\)变小。也就是说，上式中，我们希望\(f(\theta) \lt f(\theta_0)\)。则有：

\[f(\theta) - f(\theta_0) \approx \eta v \cdot \nabla f(\theta_0) \lt 0 \]

因为\(\eta\)为标量，且一般设定为正值，所以可以忽略，不等式变成了：

\[v \cdot \nabla f(\theta_0) \lt 0 \]

上面这个不等式非常重要！\(v\)和\(\nabla f(\theta_0)\)都是向量，\(\nabla f(\theta_0)\)是当前位置的梯度方向，\(v\)表示下一步前进的单位向量，是需要我们求解的，有了它，就能根据\(\theta - \theta_0 = \eta v\)确定\(\theta_0\)值了。

想要两个向量的乘积小于零，我们先来看一下两个向量乘积包含哪几种情况：

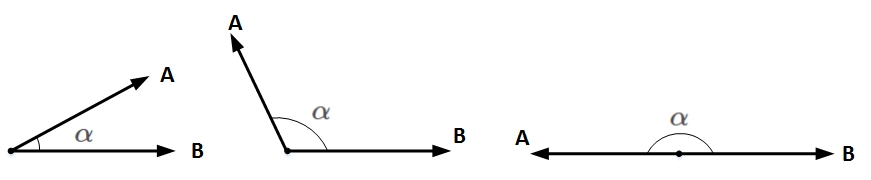
图12 两个向量乘积

\(A\)和\(B\)均为向量，\(\alpha\)为两个向量之间的夹角。\(A\)和\(B\)的乘积为：

\[A \cdot B=||A||\cdot||B|| \cdot cos(\alpha) \]

\(||A||\)和\(||B||\)均为标量，在\(||A||\)和\(||B||\)确定的情况下，只要\(cos(\alpha)=−1\)，即\(A\)和\(B\)完全反向，就能让\(A\)和\(B\)的向量乘积最小（负最大值）。

顾名思义，当\(v\)与\(\nabla f(\theta_0)\)互为反向，即\(v\)为当前梯度方向的负方向的时候，能让\(v\cdot \nabla f(\theta_0)\)最大程度地小，也就保证了\(v\)的方向是局部下降最快的方向。

知道\(v\)是\(\nabla f(\theta_0)\)的反方向后，可直接得到：

\[v=-\frac{\nabla f(\theta_0)}{||\nabla f(\theta_0)||} \]

之所以要除以\(\nabla f(\theta_0)\)的模\(||\nabla f(\theta_0)||\)，是因为\(v\)是单位向量。

求出最优解\(v\)之后，带入到\(\theta - \theta_0 = \eta v\)中，得：

\[\theta=\theta_0-\eta\frac{\nabla f(\theta_0)}{||\nabla f(\theta_0)||} \]

一般地，因为\(||\nabla f(\theta_0)||\)是标量，可以并入到步进因子\(\eta\)η中，即简化为：

\[\theta=\theta_0-\eta\nabla f(\theta_0) \]

这样，我们就推导得到了梯度下降算法中\(\theta\)的更新表达式。

 

 

参考来源：

1）https://blog.csdn.net/red_stone1/java/article/details/80212814