机器学习笔记-Logistic回归

Logistic回归

---

目录

1. 广义线性模型
2. Logistic回归
3. Logistic回归系数估计
4. 总结

---

1. 广义线性模型

在前面的笔记中，我们已经了解了线性模型。线性模型虽然简单，却有丰富的变化。例如，对于样例\((x,y), y\in R\)，\(x\)表示特征向量。当我们希望线性模型的预测值逼近真实标记\(y\)时，就得到了线性回归模型。这里，我们将线性回归模型简写为

\[y = w^Tx + b \tag{1} \]

可否令模型预测值逼近\(y\)的衍生物呢？譬如说，假设我们认为示例所对应的输出标记是在指数尺度上变化，那就可将输出标记的对数作为线性模型逼近的目标， 即

\[ln\: y = w^Tx + b \tag{2} \]

这就是“对数线性回归”(log-linear regression)，它实际上是在试图让\(e^{w^Tx+b}\)逼近\(y\)。式\((2)\)在形式上仍是线性回归，但实质上已是在求取输入空间到输出空间的非线性函数映射，如图1所示. 这里的对数函数起到了将线性回归模型的预测值与真实标记联系起来的作用。

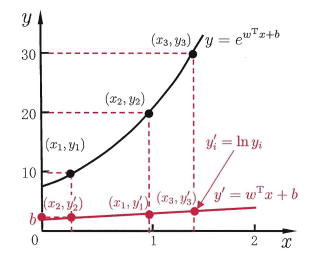
图1 对数线性回归示意图

更一般地，考虑单调可微函数\(g(\cdot)\)，令

\[y=g^{-1}(w^Tx+b) \tag{3} \]

这样得到的模型称为“广义线性模型” (generalized linear model)，其中函数\(g(\cdot)\)称为"联系函数" (link function). 显然，对数线性回归是广义线性模型在\(g(\cdot) = ln(\cdot)\)时的特例。广义线性模型的参数估计常通过加权最小二乘法会极大似然法进行。

2. Logistic回归

我们知道，可以使用线性模型进行回归学习，但是要做的是分类任务该怎么办？答案就蕴涵在式\((3)\)的广义线性模型中：只需要找一个单调可微函数将分类任务的真实标记\(y\)与线性回归模型的预测值联系起来。

考虑二分类任务，其输出标记\(y \in \{0,1\}\)，而线性回归模型产生的预测值\(z=w^Tx+b\)是实值，于是，我们需要将实值\(z\)转换为\(0/1\)值。最理想的是“单位阶跃函数”(unit-step function)

\[y = \begin{cases} \; 0, & z\lt 0; \\ 0.5, & z = 0; \\ \; 1, & z\gt 0; \end{cases} \tag{4}\]

即若预测值\(z\)大于0就判为正例，小于0则判为反例，预测值为临界值0时则可以任意判别，如图2所示。

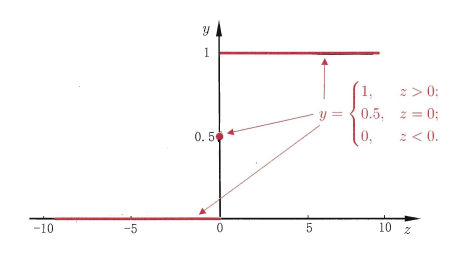
图2 单位阶跃函数

但从图2可看出，单位阶跃函数不连续，因此不能直接用作式\((3)\)中的\(g^{-}(\cdot)\)。于是我们希望找到能在一定程度上近似单位阶跃函数的“替代函数”，并希望它单调可微。

那么，这个替代函数是什么呢？

我们先说一个概念，事件的几率(odds)，是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是\(p\)，那么该事件的几率是\(p/(1-p)\)。取该事件发生几率的对数，定义为该事件的对数几率(log odds)或logit函数：

\[logit(p) = log \cfrac{p}{1-p} \tag{5} \]

这里为什么要定义对数几率呢？事件发生的概率\(p\)的取值范围是\([0,1]\)，所以计算出来的几率的取值范围是零到正无穷。而通过取对数，便可以将取值范围转换到整个实数范围内，如图3所示：

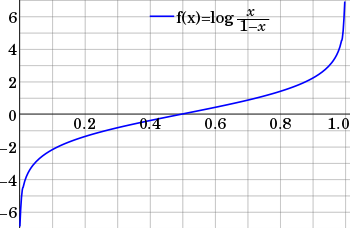
图3 Logit函数

那么，我们将输出转换到整个实数范围内的目的是什么呢？这时，回想一下我们的任务：找一个替换函数，将线性模型产生的预测值\(z=w^Tx+b\)（显然该值是实数范围内的值）转换为\(0/1\)值。因此，我们可以将对数几率记为输入特征值的线性表达式：

\[logit(p) = w_1x_1+w_2x_2,\dots,+w_mx_m + b = \sum_{i=1}^mw_ix_i+b = w^Tx+b \tag{6} \]

其中，\(p\)表示事件发生的概率，依据此概率我们能得到事件发生的对数几率。但是，我们的初衷是做分类器，简单点说就是通过输入特征来判定该实例属于哪一类别或者属于某一类别的概率。所以我们取logit函数的反函数，\(z=w^Tx+b\)为输入，\(p\)为输出，经如下推导：

\[log\cfrac{p}{1-p} = w^Tx+b = z \tag{7} \]

对式\((7)\)取反，则有

\[p = y = \cfrac{1}{1+e^{-z}} \tag{8} \]

式\((8)\)就是Logistic函数，如图4所示，Logistic函数是一种“Sigmoid函数”，即形似\(S\)的函数。它将\(z\)值转化为一个接近\(0\)或\(1\)的\(y\)值，并且其输出值在\(z=0\)附近变化很陡。将该函数作为\(g^{-}(\cdot)\)代入式\((3)\)，得到

\[y = \cfrac{1}{1+e^{-(w^Tx+b)}} \tag{9} \]

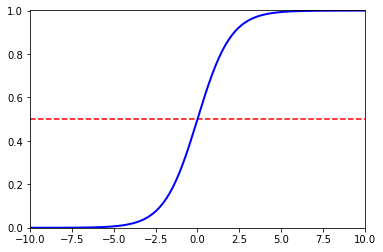
图4 Logistic函数

此时，若将\(y\)视为样本\(x\)作为正例的可能性，则\(1-y\)是其反例可能性，两者的比值就是之前描述的几率，反应了\(x\)作为正例的相对可能性。由此可以看出式\((9)\)实际上是在用线性回归模型的预测结果去逼近真实标记\(y\)的对数几率，因此，其对应的模型称为“对数几率回归”(logistic regression，亦称logit regression)，很多时候中文译为逻辑回归或逻辑斯谛回归。

那么对于式\((9)\)，我们可以这样理解：为了实现logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入函数中。进而得到一个范围在0-1之间的数值。最后设定一个阈值，在大于阈值时判定为1，否则判定为0。以上便是logistic回归算法的思想，公式就是分类器的函数形式。

3. Logistic回归系数估计

我们已经确定了logistic分类函数，有了分类函数，我们输入特征向量就可以得出实例属于某个类别的概率。但这里有个问题，回归系数我们是不确定的。正如我们想的那样，我们需要求得最优的回归系数，从而使得分类器尽可能的精确。下面我们来看看如何确定式\((9)\)中\(w\)和\(b\)。若将式\((9)\)中的\(y\)视为类后验概率估计\(p(y=1|x)\)，则经过推导我们可以得到（注：这里我们使用机器学习中常用的自然对数，下同）

\[ln \cfrac{p(y=1|x)}{p(y=0|x)} = w^Tx+b \tag{10} \]

二分类任务中，\(p(y=1|x) = 1- p(y=0|x)\)，于是有

\[p(y=1|x) = \cfrac{e^{w^Tx+b}}{1+e^{w^Tx+b}} \tag{11} \]

\[p(y=0|x) = \cfrac{1}{1+e^{w^Tx+b}} \tag{12} \]

于是，我们可通过极大似然法(maximum likelihood method)来估计\(w\)和\(b\)。给定数据集\(\{(x_i, y_i)\}_{i=1}^m\)， logistic回归模型最大化似然函数\(\mathcal{L}\)，假设数据集中的每个样本都是独立的，则有

\[\mathcal{L}(w,b) = \prod_{i=1}^mp(y_i|x_i;w,b) \tag{13} \]

于是有最大化对数似然(log-likelihood)

\[\ell(w,b) = \sum_{i=1}^m ln \,p(y_i|x_i;w,b) \tag{14} \]

即令每个样本属于其真实标记的概率越大越好。为便于讨论，令\(\beta=(w;b)\)，\(\hat{x}=(x;1)\)，则\(w^Tx+b\)可以写成\(\beta^T\hat{x}\)。再令\(p_1(\hat{x};\beta)= p(y=1|\hat{x};\beta)\)，\(p_0(\hat{x};\beta)= p(y=0|\hat{x};\beta) = 1-p_1(\hat{x};\beta)\)，则式\((14)\)中的似然项可重写为

\[p(y_i|x_i;w,b) = y_ip_1(\hat{x};\beta) + (1-y_i)p_0(\hat{x};\beta) \tag{15} \]

或

\[p(y_i|x_i;w,b) = (p_1(\hat{x};\beta))^{y_i} + (p_0(\hat{x};\beta))^{1-y_i} \tag{16} \]

其中\(y_i \in \{0,1\}\)，根据式\((11)\)和\((12)\)我们有\(p_1(\hat{\boldsymbol x}_i;\boldsymbol{\beta})=\cfrac{e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}}{1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}},p_0(\hat{\boldsymbol x}_i;\boldsymbol{\beta})=\cfrac{1}{1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}}\)，再将式\((16)\)代入\((14)\)可得

\[\begin{aligned} \ell(\boldsymbol{\beta})&=\sum_{i=1}^{m}\ln\left([p_1(\hat{\boldsymbol x}_i;\boldsymbol{\beta})]^{y_i}[p_0(\hat{\boldsymbol x}_i;\boldsymbol{\beta})]^{1-y_i}\right) \\ &=\sum_{i=1}^{m}\left[y_i\ln\left(p_1(\hat{\boldsymbol x}_i;\boldsymbol{\beta})\right)+(1-y_i)\ln\left(p_0(\hat{\boldsymbol x}_i;\boldsymbol{\beta})\right)\right] \\ &=\sum_{i=1}^{m} \left \{ y_i\left[\ln\left(p_1(\hat{\boldsymbol x}_i;\boldsymbol{\beta})\right)-\ln\left(p_0(\hat{\boldsymbol x}_i;\boldsymbol{\beta})\right)\right]+\ln\left(p_0(\hat{\boldsymbol x}_i;\boldsymbol{\beta})\right)\right\} \\ &=\sum_{i=1}^{m}\left[y_i\ln\left(\cfrac{p_1(\hat{\boldsymbol x}_i;\boldsymbol{\beta})}{p_0(\hat{\boldsymbol x}_i;\boldsymbol{\beta})}\right)+\ln\left(p_0(\hat{\boldsymbol x}_i;\boldsymbol{\beta})\right)\right] \\ &=\sum_{i=1}^{m}\left[y_i\ln\left(e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}\right)+\ln\left(\cfrac{1}{1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}}\right)\right] \\ &=\sum_{i=1}^{m}\left(y_i\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i-\ln(1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i})\right) \end{aligned} \tag{17}\]

由于此式仍为极大似然估计的似然函数，最大化似然函数等价于最小化似然函数的相反数，也即在似然函数前添加负号即可，于是得到

\[\ell(\boldsymbol{\beta})=\sum_{i=1}^{m}(-y_i\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i+\ln(1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i})) \tag{18} \]

式\((18)\)是关于\(\beta\)的高阶可导连续凸函数，根据凸优化理论，经典的数值优化算法如梯度下降法 (gradient descent method) 、牛顿法(Newton method) 等都可求得其最优解。于是就得到

\[\beta^* = arg\smash{\min_\beta}\ell(\beta) \tag{19} \]

以牛顿法为例，其第\(t+1\)轮迭代解的更新公式为

\[\beta^{t+1} = \beta^{t} - \left(\cfrac{\partial^2\ell(\beta)}{\partial \beta \partial \beta^T}\right)^{-1}\cfrac{\partial\ell(\beta)}{\partial \beta} \tag{20} \]

其中，关于\(\beta\)的一阶、二阶导数分别为

\[\cfrac{\partial\ell(\beta)}{\partial \beta} = -\sum_{i=1}^{m}\hat{x}_i(y_i-p_1(\hat{x}_i;{\beta})) \tag{21} \]

\[\cfrac{\partial^2\ell(\beta)}{\partial \beta \partial \beta^T} = -\sum_{i=1}^{m}\hat{x}_i \hat{x}_i^Tp_1(\hat{x}_i;{\beta})(1-p_1(\hat{x}_i;{\beta})) \tag{22} \]

另一种常见的优化算法是梯度下降：首先，我们令\(z=w^Tx+b = \sum_{i=1}^mw_ix_i + b\)，\(\phi(z) = \frac{1}{1+e^{-z}}\)，推导一下就会发现其实\(\phi(z)\)和式\((11)\)是等价的，根据式\((17)\)将目标函数写成

\[\ell(w) = \sum_{i=1}^{m}\left(-y_i\ln\left(\phi(z_i)\right)-(1-y_i)\ln\left(1-\phi(z_i)\right)\right) \tag{23} \]

接下来我们使用梯度下降求最小值。首先，计算对数似然函数对第\(j\)个权重的偏导

我们可以推导得到

\[\begin{aligned} \cfrac{\partial}{\partial z}\phi(z) &= \cfrac{\partial}{\partial z}\cfrac{1}{1+e^{-z}} \\ &= \cfrac{1}{(1+e^{-z})^2} e^{-z} \\ &= \cfrac{1}{1+e^{-z}}(1-\cfrac{1}{1+e^{-z}}) \\ &= \phi(z)(1-\phi(z)) \end{aligned} \tag{24}\]

于是有

\[\begin{aligned} \cfrac{\partial}{\partial w_j}\ell(w) &= \cfrac{\partial}{\partial \phi(z)}\ell(w)\cfrac{\partial}{\partial z}\phi(z)\cfrac{\partial}{\partial w_j}z \\ &= \sum_{i=1}^m\left((-\cfrac{y_i}{\phi(z_i)}+-\cfrac{1-y_i}{1-\phi(z_i)})\phi(z_i)(1-\phi(z_i))\cfrac{\partial}{\partial w_j}z\right) \\ &= \sum_{i=1}^m\left(-y_i(1-\phi(z_i))+(1-y_i)\phi(z_i)\right)x_{ij} \\ &= \sum_{i=1}^m\left(-(y_i-\phi(z_i))\right)x_{ij} \end{aligned} \tag{25}\]

我们的目标是求得使目标函数最小化的权重\(w\)，所以按梯度下降的方向不断的更新权重：

\[w_j := w_j - \eta\sum_{i=1}^m\left(y_i-\phi(z_i)\right)x_{ij} \tag{26} \]

注意，以上只是其中一个权重的更新，而梯度下降法应该是同时更新所有的权重的。

4. 总结

Logistic回归是一种广义线性回归模型，特别需注意到，虽然它的名字是"回归"，但实际却是一种分类学习方法。这种方法有很多优点，例如

• 它是直接对分类可能性进行建模，无需事先假设数据分布，这样就避免了假设分布不准确所带来的问题;
• 它不是仅预测出"类别"，而是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用;
• 此外，logistic函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解。

logistic回归是一种二分类算法，它用logistic函数预测出一个样本属于正例的概率值。预测时，并不需要真的用logistic函数映射，而只需计算一个线性函数，因此是一种线性模型。训练时，采用了极大似然估计，优化的目标函数是一个凸函数，因此能保证收敛到全局最优解。虽然有概率值，但logistic回归是一种判别模型而不是生成模型，因为它并没有假设样本向量\(x\)所服从的概率分布，即没有对\(p(x, y)\)建模，而是直接预测类后验概率\(p(y|x)\)的值。

推广到多类别

logistic回归只能用于二分类问题，将它进行推广可以得到处理多分类问题的softmax回归，思路类似，采用指数函数进行变换，然后做归一化。这种变换在神经网络尤其是深度学习中被广为使用，对于多分类问题，神经网络的最后一层往往是softmax层（不考虑损失函数层，它只在训练时使用）。

 

 

参考来源：

1）机器学习-周志华
2）https://blog.csdn.net/tian_tian_hero/article/details/89409472
3）https://cloud.tencent.com/developer/article/1339818