L2正则化、L1正则化与稀疏性
[抄书] 《百面机器学习：算法工程师带你去面试》
为什么希望模型参数具有稀疏性呢？稀疏性，说白了就是模型的很多参数是0。这相当于对模型进行了一次特征选择，只留下一些比较重要的特征，提高模型的泛化能力，降低过拟合的可能。在实际应用中，机器学习模型的输入动辄几百上千万维，稀疏性就显得更加重要，谁也不希望把这上千万维的特征全部搬到线上去。如果你真的要这样做的话，负责线上系统的同事可能会联合运维的同学一起拿着报砖来找你了。 要在线上毫秒级的响应时间要求下完成干万维特征的提取以及模型的预测，还要在分布式环境下在内存中驻留那么大一个模型，估计他们只能高呼“臣妾做不到啊”。
L2正则化、L1正则化与稀疏性的原理是什么？
角度 1：解空间形状
如图1所示，在二维的情况下，黄色的部分是L2和L1正则项约束后的解空间，绿色的等高线是凸优化问题中目标函数的等高线。由图1可知，L2正则项约束后的解空间是圆形，而L1正则项约束的解空间是多边形。显然，多边形的解空间更容易在尖角处与等高线碰撞出稀疏解。
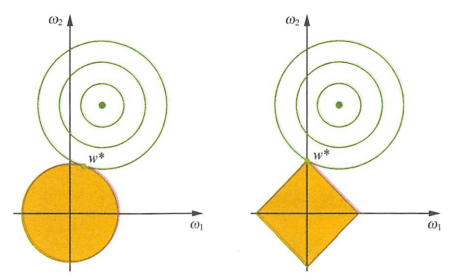
图1 L2正则化约束与L1正则化约束
上述这个解释无疑是正确的，但却不够精确，其中忽视了几个关键问题。比如，为什么加入正则项就是定义了一个解空间约束？为什么L1和L2的解空间是不同的？其实可以通过拉格朗日函数的KKT条件给出一种解释。
事实上，“带正则项”和“带约束条件”是等价的。为了约束\(w\)的可能取值空间从而防止过拟合，我们为此最优化问题加上一个约束，就是\(w\)的L2范数的平方不能大于\(m\)：
为了求解带约束条件的凸优化问题，写出拉格朗日函数
若\(w^*\)和\(\lambda^*\)分别是原问题和对偶问题的最优解，则根据KKT条件，它们应满足
仔细一看，式\((3)\)中的第一个式子不就是\(w^*\)为带L2正则项的优化问题的最优解条件嘛，而\(\lambda^*\)就是L2正则项前面的正则参数。
这时回头再看开头的问题就清晰了。 L2正则化相当于为参数定义了一个圆形的解空间（因为必须保证L2范数不能大于m），而L1正则化相当于为参数定义了一个棱形的解空间。 如果原问题目标函数的最优解不是恰好落在解空间内，那么约束条件下的最优解一定是在解空间的边界上， 而L1 “棱角分明”的解空间显然更容易与目标函数等高线在角点碰撞，从而产生稀疏解。
角度 2：函数叠加
第二个角度试图用更直观的图示来解释L1产生稀疏性这一现象。仅考虑一维的情况，多维情况是类似的，如图2所示。假设棕线是原始目标函数\(L(w)\)的曲线图，显然最小值点在蓝点处，且对应的\(w^*\)值非0。
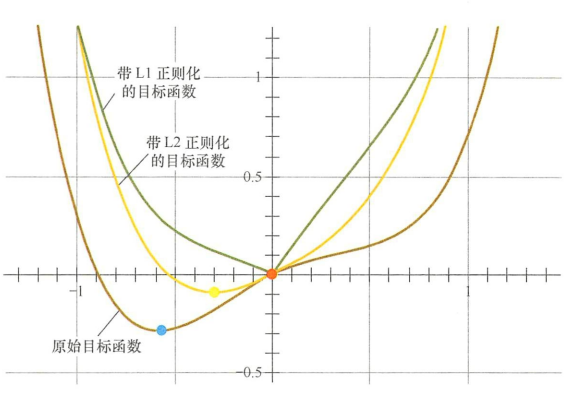
图2 函数曲线图
首先，考虑加上L2正则化项，目标函数变成\(L(w)_Cw^2\)，其函数曲线为黄色。此时，最小值点在黄点处，对应的\(w^*\)的绝对值减小了，但仍然非0。
然后，考虑加上Ll正则化顷，目标函数变成\(L(w)+C|w|\)，其函数曲线为绿色。此时， 最小值点在红点处，对应的\(w^*\)是0，产生了稀疏性。
产生上述现象的原因也很直观。加入L1正则顶后，对带正则项的目标函数求导，正则项部分产生的导数在原点左边部分是\(-C\)，在原点右边部分是\(C\)，因此，只要原目标函数的导数绝对值小于\(C\)，那么带正则项的目标函数在原点左边部分始终是递减的，在原点右边部分始终是递增的，最小值点自然在原点处。相反，L2正则项在原点处的导数是0，只要原目标函数在原点处的导数不为0，那么最小值点就不会在原点，所以L2只有减小 \(w\)绝对值的作用，对解空间的稀疏性没有贡献。
在一些在线梯度下降算法中，往往会采用截断梯度法来产生稀疏性，这同L1正则顶产生稀疏性的原理是类似的。
角度 3：贝叶斯先验
从贝叶斯的角度来理解L1正则化和L2正则化，简单的解释是，L1正则化相当于对模型参数\(w\)引入了拉普拉斯先验，L2正则化相当于引入了高斯先验，而拉普拉斯先验使参数为0的可能性更大。图3是高斯分布曲线图。由图可见，高斯分布在极值点(0点)处是平滑的，也就是高斯先验分布认为\(w\)在极值点附近取不同值的可能性是接近的。这就是L2正则化只会让\(w\)更接近0点，但不会等于0的原因。
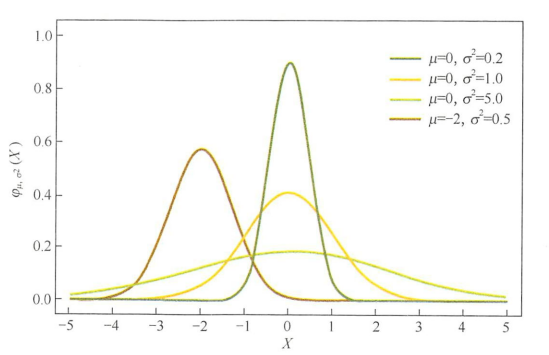
图3 高斯分布曲线
相反，图4是拉普拉斯分布曲线图。由图可见，拉普拉斯分布在极值点（0点）处是一个尖峰，所以拉普拉斯先验分布中参数\(w\)取值为0的可能性要更高。在此我们不再给出L1 和L2正则化分别对应拉普拉斯先验分布和高斯先验分布的详细证明。
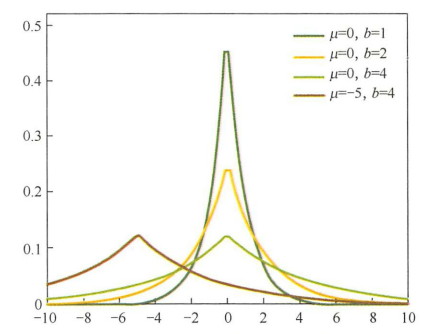
图4 拉普拉斯分布曲线图
posted on
