多项式回归

线性回归模型形式简单，有很好的解释性，但它有不少假设前提，其中最重要的一条就是数据之间存在着线性关系，但是在实际生活中，很多数据之间是非线性关系，虽然也可以用线性回归拟合非线性回归，但是效果将会很差。这个时候可以尝试使用多项式回归。多项式回归中，加入了特征的更高次方（例如平方项或立方项），也相当于增加了模型的自由度，用来捕获数据中非线性的变化。添加高阶项的时候，也增加了模型的复杂度。随着模型复杂度的升高，模型的容量以及拟合数据的能力增加，可以进一步降低训练误差，但导致过拟合的风险也随之增加。

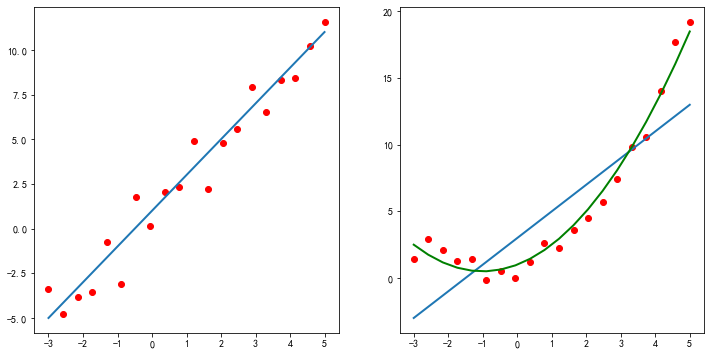
图1 线性回归与多项式回归

如图1所示，左图数据呈现出线性关系，此时用线性回归可以得到较好的拟合效果，如图中的蓝色直线。右图数据则呈现出非线性的关系，显然直线不能得到好的拟合效果，可以通过多项式回归模型得到较好的拟合结果。

因为图中的数据是人工生成的，所以右图中的绿色曲线模型参数是已知的，其多项式方程为\(y=0.5x^2+x+1\)。

1. 多项式回归的一般形式

在多项式回归中，最重要的参数是最高次方的次数。假设最高次方的次数是\(n\)，且样本只有一个特征时，其多项式回归方程表示为：

\[h_\theta(x) = \theta_0+\theta_1x^1+\dots+\theta_{n-1}x^{n-1}+\theta_nx^n \tag{1} \]

如果令\(x_0=1\)，在多样本的情况下，可以写成向量化的形式：

\[h_\theta(x) = X\theta \tag{2} \]

其中\(X\)是大小为\(m\times (n+1)\)的矩阵，\(\theta\)是大小为\((n+1)\times 1\)的矩阵。在这里虽然只有一个特征\(x\)以及\(x\)的不同次方，但是也可以将\(x\)的高次方当做一个新特征。与多元回归分析唯一不同的是，这些特征之间是高度相关的，而不是通常要求的那样是相互对立的。

如果样本不止一个特征，以只有两个特征的2次方多项式的回归模型为例：

\[h_θ(x_1,x_2)=θ_0+θ_1x_1+θ_2x_2+θ_3x^2_1+θ_4x^2_2+θ_5x_1x_2 \tag{3} \]

其他多特征多次方的方程以此类推即可。

在这里有个问题，如果假设中出现了高阶项，那么这个模型还是线性模型吗？此时看待问题的角度不同，得到的结果也不同。如果把上面的假设看成是特征\(x\)的方程，那么该方程就是非线性方程；如果看成是参数\(\theta\)的方程，那么\(x\)的高阶项都可以看做是对应\(\theta\)的参数，那么该方程就是线性方程。很明显，在线性回归中采用了后一种解释方式。因此多项式回归仍然是参数的线性模型。

回到线性模型，\(h_θ(\pmb x)=θ_0+θ_1x_1+...+θ_nx_n\), 如果我们令式\((3)\)中的\(x_0=1,x_1=x_1,x_2=x_2,x_3=x^2_1,x_4=x_2^2,x_5=x_1x_2\) ,这样我们就得到了下式：

\[h_θ(x_1,x_2)=θ_0+θ_1x_1+θ_2x_2+θ_3x_3+θ_4x_4+θ_5x_5 \]

可以发现，我们又重新回到了线性回归，这是一个五元线性回归，可以用线性回归的方法来完成算法。对于每个二元样本特征\((x1,x2)\),我们得到一个五元样本特征\((1,x_1,x_2,x^2_1,x_2^2,x_1x_2)\)，通过这个改进的五元样本特征，我们把非线性回归的函数变回了线性回归。

2. 多项式回归示例

下面主要使用了numpy、matplotlib和scikit-learn，如下：

# python 3.6
# sklearn 0.20.3

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import Pipeline

接下来生成只有一个特征，共10个样本的训练数据，使用\(y=0.5x^2+x+2\)并加入一些随机误差生成对应的输出值。

rng = np.random.RandomState(1)
# 生成样本数据
x = np.linspace(-3, 7, 10)
y = 0.5 * x**2 + x + 2 + rng.normal(0, 1.2, 10)
# 转换成矩阵的形式
X = x[:,np.newaxis]
y = y[:,np.newaxis]

# 将样本点显示在坐标轴上，如图2所示
plt.figure(figsize=(8, 6))
plt.scatter(X, y, color="r")
plt.xlabel("X")
plt.ylabel("y")
# plt.show()

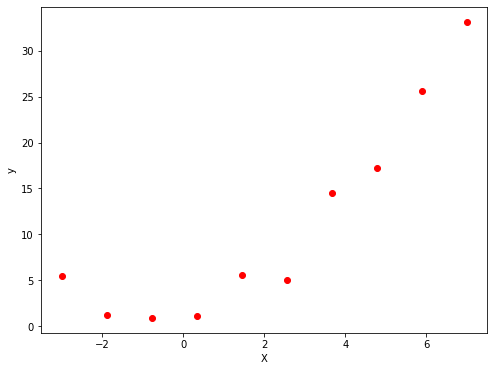
图2 生成的原始数据

2.1 使用直线方程拟合

下面先使用直线方程拟合生成的数据：

lin_reg = LinearRegression()
lin_reg.fit(X, y)
print(lin_reg.intercept_, lin_reg.coef_)  
# [5.05753609] [[2.95924372]]

# 绘制出拟合数据得到的直线，如图3所示
X_plot = np.linspace(-3, 7, 200).reshape(-1, 1)
y_plot = lin_reg.coef_*X_plot + lin_reg.intercept_

plt.figure(figsize=(8, 6))
plt.plot(X_plot, y_plot, color='b', linewidth=2)
plt.scatter(X, y, color='r')
plt.xlabel('X')
plt.ylabel('y')
# plt.show()

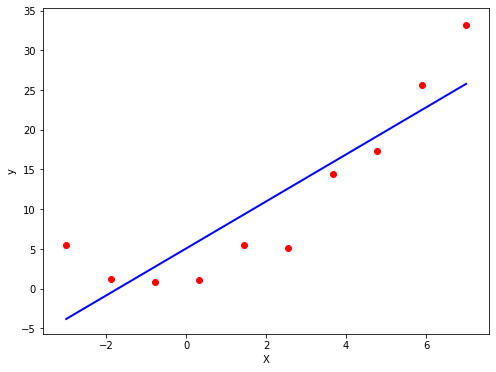
图3 直线拟合效果

可以使用函数"mean_squared_error"来计算模型在训练数据上的均方误差(MSE):

print("线性回归模型的MSE：{}".format(mean_squared_error(y, lin_reg.predict(X))))
# 线性回归模型的MSE：25.902093991686804

2.2 使用多项式回归

为了拟合2次方程，需要有特征\(x^2\)的数据，这里可以使用函数"PolynomialFeatures"来获得：

# 参数degree设定2次方项
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
# print(X_poly)

# 训练模型
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
print(lin_reg.intercept_, lin_reg.coef_)
# [1.6761218] [[0.77246083 0.54669572]]

# 将拟合得到的曲线绘制出来，如图4所示
X_plot = np.linspace(-3, 7, 200).reshape(-1, 1)
X_plot_poly = poly_features.fit_transform(X_plot)
y_plot = np.dot(X_plot_poly, lin_reg.coef_.T) + lin_reg.intercept_
plt.figure(figsize=(8, 6))
plt.plot(X_plot, y_plot, color='b', linewidth=2)
plt.scatter(X, y, color='r')
plt.xlabel('X')
plt.ylabel('y')
# plt.show()

图4 多项式拟合数据

print("多项式回归模型的MSE：{:.3f}".format(mean_squared_error(y, lin_reg.predict(X_poly))))
多项式回归模型的MSE：1.850

从上述代码中，我们得到了多项式回归模型的参数，即多项式方程为\(h(x)=0.55x^2+0.77x+1.68\)，而我们生成数据使用的方程为\(y=0.5x^2+x+2\)。可以看出两个方程之间还是比较相近的。

如上所示，利用多项式回归，损失函数MSE的值下降到了1.85。通过观察代码，可以发现训练多项式方程与直线方程唯一的差别是输入的训练集\(X\)的差别。在训练直线方程时直接输入了\(X\)的值，在训练多项式方程的时候，还添加了我们计算出来的\(x^2\)这个“新特征”的值（由于\(x^2\)完全是由\(x\)的值确定的，因此严格意义上来讲此时该模型只有一个特征\(x\)）。

此时有个非常有趣的问题：假如一开始得到的数据就是上面代码中"X_poly"的样子，且不知道\(x_1\)与\(x_2\)之间的关系。此时相当于我们有10个样本，每个样本具有\(x_1,x_2\)两个不同的特征。这时假设函数为：

\[h_\theta(x)=θ_0+θ_1x_1+θ_2x_2 \]

直接按照二元线性回归方程来训练，也可以得到上面同样的结果（\(\theta\)的值）。如果在相同情况下，收集到了新的数据，可以直接带入上面的方程进行预测。唯一不同的是，我们不知道\(x_2=x^2_1\)这个隐含在数据内部的关系，所有也就无法画出图4中的这条曲线。一旦了解到了这两个特征之间的关系，数据的维度就从3维下降到了2维（包含截距项\(\theta_0\)）。

2.3 多项式阶数与过拟合

在上面实现多项式回归的过程中，通过引入高阶项\(x^2\)，训练误差从25.90下降到了1.85，减小了非常多。那么训练误差是否还有进一步下降的空间呢？答案是肯定的，通过继续增加更高阶的项，训练误差可以进一步降低。通过尝试，当最高阶项为\(x^9\)时，训练误差几乎等于0了。

下面是测试不同阶数(degree)产生的拟合效果：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import Pipeline

mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
np.set_printoptions(suppress=True)

rng = np.random.RandomState(1)
N = 10
x = np.linspace(-3, 7, N)
x = np.sort(x)
y = 0.5 * x**2 + x + 2 + rng.normal(0, 1.2, N)
x.shape = -1, 1
y.shape = -1, 1

model = Pipeline([
    ('poly', PolynomialFeatures()),
    ('linear', LinearRegression())])

plt.figure(figsize=(8, 6), facecolor='w')
# 多项式的阶数
d_pool = np.arange(1, N, 1)

m = d_pool.size
# 配置颜色
clrs = []
rdbu = mpl.cm.get_cmap("RdYlBu", m)
for c in np.linspace(0, 1, m):
    clrs.append(rdbu(c))

plt.scatter(x, y, color="r")

for i, d in enumerate(d_pool):
    model.set_params(poly__degree=d)
    model.fit(x, y)
    # lin = model.get_params('linear')['linear']

    x_hat = np.linspace(x.min(), x.max(), num=100)
    x_hat.shape = -1, 1
    y_hat = model.predict(x_hat)
    s = mean_squared_error(y, model.predict(x))

    plt.plot(x_hat, y_hat, color=clrs[i], lw=2, label=('%d阶，train mse=%.3f' % (d, s)))
    plt.legend(loc='upper left')
    plt.grid(True)

    plt.xlabel('X', fontsize=14)
    plt.ylabel('Y', fontsize=14)
    
plt.tight_layout(1, rect=(0, 0, 1, 0.95))
plt.show()

此时，我们绘制出不同多项式阶数拟合效果的图像，如图5所示：

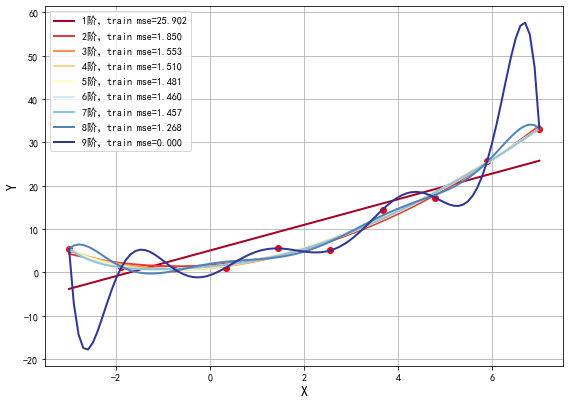
图5 不同阶数拟合数据

由图5可以看到，当多项式阶数逐渐增加时，训练误差逐渐减低。当阶数为9时，函数图像几乎穿过了每一个样本点，所有的训练样本都落在了拟合的曲线上，训练误差接近于0。可以说是近乎完美的模型了。但是，这样的曲线与我们最开始数据的来源（一个二次方程加上一些随机误差）差异非常大。如果从相同来源再取一些样本点，使用该模型预测会出现非常大的误差。类似这种训练误差非常小，但是新数据点的测试误差非常大的情况，就叫做模型的过拟合。过拟合出现时，表示模型过于复杂，过多考虑了当前样本的特殊情况以及噪音（模型学习到了当前训练样本非全局的特性），使得模型的泛化能力下降。

出现过拟合一般有以下几种解决方式：

降低模型复杂度，例如减小上面例子中的degree；
降维，减小特征的数量；
增加训练样本，在现实机器学习任务中很难办到；
添加正则化项.

防止模型过拟合是机器学习领域里最重要的问题之一。鉴于该问题的普遍性和重要性，在满足要求的情况下，能选择简单模型时应该尽量选择简单的模型。

参考来源：
1）https://www.cnblogs.com/Belter/p/8530222.html
2）https://blog.csdn.net/qq_25560849/article/details/80543180
3）https://www.cnblogs.com/pinard/p/6004041.html

posted on 2020-05-29 14:47 WarningMessage 阅读(1513) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部