线性回归
目录
1. 线性回归的引入
假设现在我们有一个记录个人收入的数据集,其中记录了30个人的收入与各自的受教育年限的关系。如图1所示,坐标横轴表示受教育年限,纵轴表示收入。从图中可以看到,随着受教育年限的增加,收入也在相应的增加。我们猜测数据的分布或许服从一条直线,如图1所示:
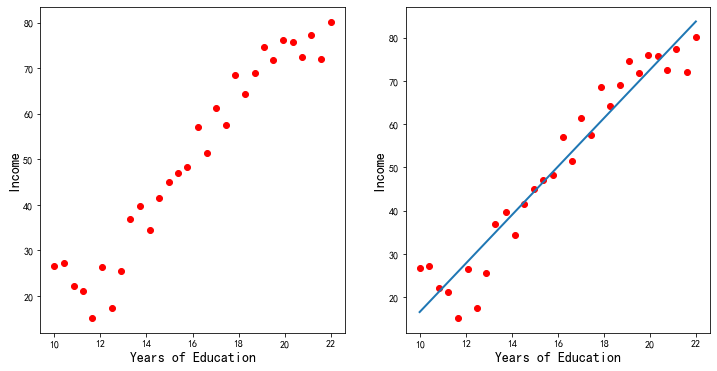
图1
那么,如何去得到这条直线呢?我们可以将这条直线写成:
我们怎么找到\(w\)和\(b\),进而确定这条直线呢?
接下来,考虑另一个问题,我们知道,个人的收入不仅跟受教育年限有关,可能还跟个人的专业资历有关,比如同样的受教育年限,但是,不同时间的专业资历收入通常是不同的。然后我们怎么做呢?假设我们的数据如下:
| Education | Seniority | Income |
|---|---|---|
| 21.586207 | 113.103448 | 99.917173 |
| 18.275862 | 119.310345 | 92.579135 |
| 12.068966 | 100.689655 | 34.678727 |
| 17.034483 | 187.586207 | 78.702806 |
| 19.931034 | 20.000000 | 68.009922 |
| ... | ... | ... |
这里,如果用\(x_1\)表示特征受教育年限,\(x_2\)表示特征专业资历,\(y\)表示收入。我们认为\(w_1x_1+w_2x_2\)基本上可以预测\(y\),实际问题中可能还要加上截距\(b\),即应该能够得到一个模型:
输入一个特征向量\(\pmb x\),得到一个\(f(\pmb x)\)。如果这个\(f(x)\)与\(y\)相等或接近,那么,这就是我们希望得到的模型,如图2所示的平面。
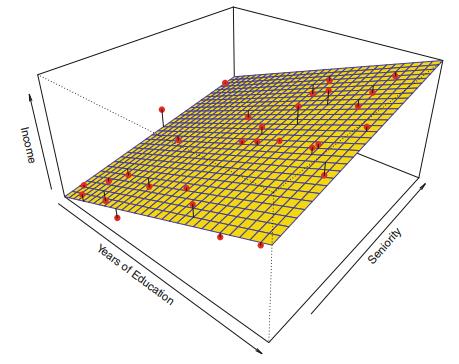
图2
观察上述模型公式,这个模型可以看做是向量的线性组合,即:
其中,令\(b=w_0\),\(x_0\)恒等于\(1\)。可以得到
显然,我们可以将特征向量扩展到\(d\)维,比如,前面的数据中,可能还有年龄、性别、所在地区等等,都与个人收入有关,所以通常情况下并不是只有一个或两个特征,可能会有多个特征,这里只是举例说明线性模型的形式,但是我们在推导的过程中特征的多少并不会对结果产生影响,即就公式推导而言结果是与维度无关的。于是我们得到
这个模型其实就是线性回归的模型。其中,\(\pmb x\)表示样本,是已知的。\(\pmb w\)是要估计的参数,是未知的。我们后面最主要的工作就是根据给定样本,来计算一下到底哪个\(w_1\),\(w_2\),...,\(w_d\)和\(b\)能够更好的对\(y\)进行预测。
2. 线性回归模型
2.1 线性模型的基本形式
给定由\(d\)个特征描述的样本\(\pmb x = (x_{1},x_{2},\dots,x_{d})\),其中\(x_i\)是\(\pmb x\)在第\(i\)个特征上的取值,线性模型(linear model)试图学的一个通过特征的线性组合来进行预测的函数,即
向量形式写成:
其中,\(\pmb w = (w_{1},w_{2},\dots,w_{d})\)。\(\pmb w\)和\(b\)学习得到后,模型就可以被确定。线性模型形式简单,易于建模。此外,由于\(\pmb w\)直观的表达了各特征在预测中的重要性,因此模型的可解释性很好。
对于线性回归而言,给定数据集\(D=\{(\pmb x_1,y_1),(\pmb x_2,y_2),\dots,(\pmb x_m,y_m)\}\),其中\(\pmb x_i = (x_{i1},x_{i2},\dots,x_{id})\),\(y_i \in R\)。线性回归试图学得一个线性模型以尽可能准确的预测实值输出标记\(y\)。
先考虑一种简单的情形:
2.2 简单线性回归
简单线性回归是一种非常简单的根据单一输入特征预测实值输出的方法,此时,我们忽略特征的下标,即数据集\(D=\{(x_i,y_i)\}_{i=1}^m\),其中\(x_i \in R\)。
此时,它假定输入与输出之间存在线性关系,线性回归试图学得:
使得 \(f(x_i) \approx y_i\)。公式(3)中的\(w\)和\(b\)是两个未知的常量,它们分别表示线性模型中的斜率和截距。\(w\)和\(b\)被称为模型的系数(coefficent)或参数(parameter)。如之前所述,一旦使用训练数据估计出了模型系数\(w\)和\(b\),我们就可以通过计算
来对给定的\(x\)进行预测了,其中,\(f(x)\)表示在给定\(x\)时对\(y\)的预测。\(w^*\)和\(b^*\)表示对未知系数的估计值。
2.1.1 系数估计
在现实问题中,\(w\)和\(b\)都是未知的。所以在用式\((4)\)做出预测之前,我们必须根据训练数据集来估计他们。现数据集\(D = \{(x_1,y_1),(x_2,y_2),\dots,(x_m,y_m)\}\)。
我们的目的是获得系数\(w\)和\(b\)的估计,以使得对于\(i = 1,2,\dots,m\)有\(y_i \approx f(x_i) = w^*x_i+b^*\)。换句话说,我们希望找到斜率\(w\)和截距\(b\),使得由此产生的直线尽可能的接近这\(m\)个样本点,也即是说使得\(y_i\)与\(f(x_i)\)之间的差别尽可能的小。
怎么测量接近程度呢?最常用的方法是均方误差,也称为平方损失。我们试图求解一个\(w\)和\(b\)让均方误差最小化。即
基于均方误差最小化进行模型求解的方法称为“最小二乘法”(least square method)。在线性回归中,最小二乘法就是试图找一条直线,使得所有样本到直线上的欧氏距离之和最小。
求解\(w\)和\(b\)使\(E_{(w,b)}=\sum_{i=1}^m(y_i - wx_i-b )^2\)最小化的过程,称为线性回归模型的最小二乘“参数估计”(parameter estimation)。注:这里虽然用的是均方误差,但是并没有除以\(m\),因为是否除以\(m\),并不重要,我们并不关心损失函数真正的最小值是多少,而只是关心损失函数取最小值的时候模型的参数是多少。这里除以或者不除以m,最终的极值对应的模型参数是一样的。求解过程如下:
将\(E_{(w,b)}\)分别对\(w\)和\(b\)求导:
然后令式(6)和(7)为0,得到\(w\)和\(b\)最优解的闭式(closed-form)解:
其中,\(\overline{x} = \frac{1}{m} \sum_{i=1}^mx_i\)为\(x\)的均值。
2.2 多元线性回归
简单线性回归是根据单一输入特征预测实值输出的方法,但是在实践中,样本往往不止一个特征,正如开始讨论的那样。考虑开始给出的数据集\(D\),样本由\(d\)个属性描述。此时,我们要学得
使得\(f(\pmb x_i) \approx y_i\)。这称为“多元线性回归”(multivariate linear regression)。
2.2.1 系数估计
与简单线性回归一样,可以利用最小二乘法对\(\pmb w\)和\(b\)进行估计,这里我们采用向量运算。首先,令\(\pmb {\hat w}=(\pmb w,b)\),相应的数据集\(D\)变成了\(m\times{(d+1)}\)大小的矩阵\(\pmb X\),其中,每行的最后一个元素恒置为\(1\),如下:
再把标记也写成向量形式\(\pmb y = (y_1, y_2, \dots, y_m)\),则在均方误差最小化的目标下,有
令\(E_{\hat w} = (\pmb y-\pmb X \pmb{\hat w})^T(\pmb y-\pmb X \pmb{\hat w})\),即:
对\(\hat{\boldsymbol w}\)求导可得
由矩阵微分公式\(\cfrac{\partial\boldsymbol{a}^{\mathrm{T}}\boldsymbol{x}}{\partial\boldsymbol{x}}=\cfrac{\partial\boldsymbol{x}^{\mathrm{T}}\boldsymbol{a}}{\partial\boldsymbol{x}}=\boldsymbol{a},\cfrac{\partial\boldsymbol{x}^{\mathrm{T}}\mathbf{A}\boldsymbol{x}}{\partial\boldsymbol{x}}=(\mathbf{A}+\mathbf{A}^{\mathrm{T}})\boldsymbol{x}\)可得
令上式为零,可得\(\pmb {\hat w}\)最优解的闭式解。
于是得到,
其中,\((\pmb X^T\pmb X)^{-1}\)是\((\pmb X^T\pmb X)\)的逆矩阵。这要求\((\pmb X^T\pmb X)\)为满秩矩阵(full-rank matrix)或正定矩阵(postive definite matrix)。
令\(\pmb{\hat x_i} = (\pmb x_i,1)\),我们就得到了多元线性回归模型:
3. 最大似然估计和最小二乘法
3.1 线性回归中的假设
一般情况下,假设观察到一个定量的标记\(\pmb y\)和\(m\)个不同的样本,记为\(\pmb x_1,\pmb x_2,\dots,\pmb x_m\)。如果这个\(\pmb y\)与\(\pmb x\)之间有一定的关系,则可以表达成一个比较一般的形式:
这里的\(f\)是\(\pmb x_1,\pmb x_2,\dots,\pmb x_m\)的函数,它是固定的但未知,\(\pmb{\varepsilon}\)是随机误差项,与\(\pmb x\)独立,且均值为\(0\)。
如果是线性回归模型,则可表示为
其中,为了方便我们将截距\(b\)包含在了向量\(\pmb w\)中。
我们学习或训练得到的模型其实是\(f\)的一个估计,这里记作\(\hat f\)。而\(\hat f(\pmb x)\)作为\(\pmb y\)的预测,其精确性依赖于两个量,一个是可约误差,另一个是不可约误差。大体上,当所选的\(\hat f\)不是\(f\)的一个最佳估计时,对模型估计的不准确也会引起一些误差,但这个误差是可约的,因为我们实际上有能力提高\(f\)的精确度,只要选择更合适的学习方法去估计\(f\)就可能降低这种误差。然而,即使得到一个\(f\)的精准估计,对\(\pmb y\)的估计来自于表达式\(\hat f(\pmb x) = f(\pmb x)\),预测仍然存在误差。这是因为\(\pmb y\)还是一个关于\(\pmb{\varepsilon}\)的函数。按照定义,\(\pmb{\varepsilon}\)是独立于\(\pmb x\)的,不能用\(\pmb x\)去预测。因此,与\(\pmb{\varepsilon}\)有关的变量也影响到预测的准确性。这部分误差就被称为不可约误差,因为无论我们对\(f\)估计的多么准确,我们都不能减少\(\pmb{\varepsilon}\)引起的误差。这个量\(\pmb{\varepsilon}\)可能包含了对预测\(\pmb y\)有用但却不可直接观测的变量信息:由于没有测量它们,所以\(f\)不能使用这些变量去预测。量\(\pmb{\varepsilon}\)也可能包含了根本不可测的变差。
线性回归中误差项\(\pmb{\varepsilon}\)的假设:
以前面的收入数据为例,我们假设每个人的收入是相互独立的,一个人的收入高低与另一个人的收入无关。则\(\pmb{\varepsilon}_i (1\le i \le m)\)可以认为是独立同分布的,是各个未知的细节因素导致的个人收入的上下波动,如果我们将他们看作随机变量的话,当足够多的随机变量进行叠加之后形成的分布,根据中心极限定理,认为他们服从均值为\(\mu\),方差为\(\sigma^2\)的正态分布是一种比较合理的假设。其中,由于有截距项的存在,是可以使均值\(\mu=0\)的,即\(\varepsilon \sim N(0,\sigma^2)\)。如果以直线为例,即是使数据点分布在直线的两侧。
3.2 最大似然估计和最小二乘法
按照上面的假设\(\varepsilon \sim N(0,\sigma^2)\),根据正态分布的概率密度函数,我们有:
将公式\((16)\)带入可得到,
这里,我们可以这样理解,在给定了样本数据和系数的值的条件下,就可以求得\(y\)值的概率值。
但现在的问题是,不知道回归系数。式\((18)\)反应的是计算\(y\)的条件概率,如果概率值越大,则说明预测出来的\(\hat y\)会越接近于真实的\(y\),所以,现在的问题就变成了计算概率的最大值。根据样本之间对应的\(y\)是独立的假设,我们可以对其构造最大似然函数,即:
为了求解方便,我们在等式两边取对数,得到对数似然:
由于等式\((20)\)右边的前半部分是一个常数,而后半部分是一个负值,所以求解似然函数的极大值问题就转换成了求
的最小值问题。观察式\((21)\),它其实与我们前面使用的最小二乘法是一样的,见公式\((5)\)。
4. 线性回归模型评估
4.1 模型的显著性检验
通过最小二乘法我们得到了模型的系数,但是得到系数就一定能够保证模型是OK的吗?这里还需要对模型进行显著性检验,模型显著性检验的假设条件是:
零假设\(H_0: w_0=w_1=\dots=w_d=0\),即模型的所有系数都为0,输入与输出之间没有任何关系;
备择假设\(H_1: w_0, w_2, \dots, w_d\)至少有一个不为0。
我们先从图3中来理解一下几个概念:

图3
总的离差平方和:\(TSS=\sum_{i=1}^m(y_i-\overline{y})^2\);
回归离差平方和:\(RSS = \sum_{i=1}^m(\hat{y}-\overline{y})^2\);
误差平方和:\(ESS = \sum_{i=1}^m(\hat{y}-y_i)^2\)
其中,\(y_i\)表示实际的样本标记值,\(\hat{y}\)表示通过模型预测得到的值,\(\overline{y}\)表示样本标记值的均值。
由上面的计算公式可知,\(TSS=RSS+ESS\)。实际上,TSS是固定,而ESS和RSS是跟模型的预测值有关的,如果模型拟合的越好,则误差平方和(ESS)应该越小,对应的RSS越大。所以,根据这两个离差平方和就可以构造模型检验的统计量F:
其中,\(d\)和\(m-d-1\)为RSS和ESS的自由度。当我需要检验模型是否OK的时候,只需要将计算出来的统计量F与理论的值作对比,如果统计量F值大于理论的临界值,则认为可以拒绝原假设\(H_0\),即接受备注假设\(H_1\)。
4.2 参数显著性检验
上面是针对模型的显著性检验作了相关的理论说明,但模型OK(所有的偏回归系数不全为0),并不代表每一个自变量对因变量都是重要的,即每一个回归系数都是OK(所有的系数都不为0)的,所以,我们还需要对模型的每个回归系数进行显著性检验。
根据公式,我们可以推导出回归系数的期望和方差:
期望\(E(w^*) = w\)
方差\(Var(w^*) = \sigma^2(X^TX)^{-1}\)
既然有了回归系数的期望和方差,我们就可以根据标准正态分布来构造t分布了,之所以是t分布,是因为总体方差未知。当总体方差未知的时候,则使用样本方差来代替,但要付出一些代价,不再是标准正太分布,而是自由度为n-1的t分布:
接下来就是要进行参数的显著性检验了,其检验的假设条件为:
零假设\(H_0: w_j=0, j=0,1,2,\dots,d\)
备择假设\(H_1: w_j \ne 0\)
构造检验回归系数的t统计量:
其中,\(w^*_j\)是回归系数\(w_i\)的估计,\(se(w^*_j)\)是回归系数\(w_j\)的标准误,即
最终,通过计算统计量t的值与理论的\(t(n-p-1)\)值作对比,如果统计量\(t\)值大于理论的临界值,则认为可以拒绝原假设\(H_0\),否则就得接受原假设。
4.3 \(R^2\)统计量
\(R^2\)统计量是衡量拟合度的一个标准。 \(R^2\)统计量采取比例(proportion) (被解释方差的比例)形式,所以它的值总在0和1之间,与\(\pmb y\)的量级无关。\(R^2\)用下列公式计算:
其中,\(TSS=\sum(y_i-\overline{y})\)是总平方和,\(ESS=\sum_{i=1}^m(y_i-\hat {y})^2\)是误差平方和。总平方和测量输出标记\(\pmb y\)的总方差,可以认为是在执行回归分析之前\(\pmb y\)中的固有变异性。相对的,ESS测量的是进行回归后仍无法解释的变异性。因此, TSS - ESS测量的是输出标记\(\pmb y\)进行回归之后被解释的(或被消除)的变异性,而\(R^2\)测量的是\(\pmb y\)的变异中能被\(X\)解释的部分所占比例\(R^2\)统计量接近1说明回归可以解释\(\pmb y\)的大部分变异。\(R^2\)统计量接近0说明回归没有解释太多\(\pmb y\)的变异,这可能因为线性模型是错误的,也可能因为固有误差项\(\sigma^2\)较大,抑或两者兼有。
注这一节的详细内容可以参看(An Introduction to Statistical Learning with Applications in R)
5. 最小二乘法的局限性和适用场景
首先,最小二乘法需要计算\(X^TX\)的逆矩阵,有可能它的逆矩阵不存在,这样就没有办法直接用最小二乘法了,此时梯度下降法仍然可以使用。当然,我们可以通过对样本数据进行整理,去掉冗余特征。让\(X^TX\)的行列式不为0,然后继续使用最小二乘法。
第二,当样本特征\(n\)非常的大的时候,计算\(X^TX\)的逆矩阵是一个非常耗时的工作(\(n\times n\)的矩阵求逆),甚至不可行。此时以梯度下降为代表的迭代法仍然可以使用。那这个\(n\)到底多大就不适合最小二乘法呢?如果你没有很多的分布式大数据计算资源,建议超过10000个特征就用迭代法吧。或者通过主成分分析降低特征的维度后再用最小二乘法。
第三,如果拟合函数不是线性的,这时无法使用最小二乘法,需要通过一些技巧转化为线性才能使用,此时梯度下降仍然可以用。
第四,我们看到,要想求得\(\pmb {\hat w}\)的最优解,需要满足\((\pmb X^T\pmb X)\)为满秩矩阵(full-rank matrix)或正定矩阵(postive definite matrix)。但是,现实任务中\((\pmb X^T\pmb X)\)往往不是满秩矩阵。例如在许多任务中我们会遇到大量的变量,其数目甚至超过样例数,导致\(\pmb X\)的列数多于行数,\((\pmb X^T\pmb X)\)显然不满秩。此时可解出多个\(\pmb {\hat w}\),它们都能使均方误差最小化。选择哪一个解作为输出,将由学习算法的归纳偏好决定, 常见的做法是引入正则化 (regularization) 项。
参考来源:
1)机器学习 - 周志华
2)https://blog.csdn.net/denghecsdn/java/article/details/77334160
3)Prof.Andrew Ng. Machine Learning. Stanford University。
4)https://www.cnblogs.com/pinard/p/5976811.html 最小二乘法小结
5)从零开始学Python【20】--线性回归(理论部分)
6)统计学习导论 - 基于R应用


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号