机器学习笔记-距离度量与相似度(二)马氏距离

马氏距离（Mahalanobis Distance）

马氏距离(Mahalanobis Distance)是由印度统计学家马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。它考虑到数据特征之间的联系，并且是尺度无关的（scale-invariant），即独立于测量尺度。

马氏距离的定义

假设\(x\)，\(y\)是从均值向量为\(\mu\)，协方差矩阵为\(\Sigma\)的总体\(G\)中随机抽取的两个样本，定义\(x\)，\(y\)两点之间的马氏距离为：

\[d_m^2(x, y)= (x-y)^T \Sigma^{-1}(x-y) \]

定义\(x\)与总体\(G\)的马氏距离为：

\[d_m^2(x, \mu_G)= (x-\mu_G)^T \Sigma^{-1}(x-\mu_G) \]

其中，如果协方差矩阵是单位向量，也就是各维度独立同分布，马氏距离就变成了欧氏距离。

注：上面的两个表达式其实是马氏距离的平方

为什么定义马氏距离

1. 数据指标的单位对距离度量的影响

在很多机器学习问题中，样本间的特征都可以用距离去描述，比如说最常见的欧氏距离。对于欧氏距离而言，空间中任意两点\(P=(x_1, x_2, \dots, x_p)\)与\(Q=(y_1, y_2, \dots, y_p)\)之间的距离为：

\[d(P,Q)=\sqrt{(x_1-y_1)^2 + (x_2-y_2)^2 + \dots + (x_p-y_p)^2} \]

显然，当固定点\(Q\)且取值为\(0\)时，表示点\(P\)到坐标原点的距离。

欧氏距离有一个缺点，就是当各个分量为不同性质的量时(比如，人的身高与体重，西瓜的重量与体积)，“距离”的大小竟然与指标的单位有关。例如，横轴\(x_1\)代表重量（以\(kg\)为单位），纵轴\(x_2\)代表长度（以\(cm\)为单位）。有四个点\(A, B, C, D\)，如图2.1所示。

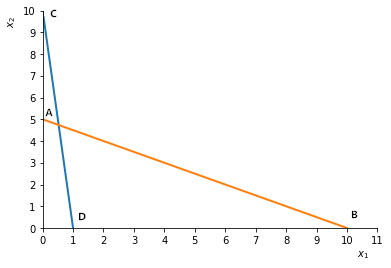
图2.1

这时

\(d(A, B) = \sqrt{5^2+10^2} = \sqrt {125}\)
\(d(C, D) = \sqrt{10^2+1^2} = \sqrt {101}\)

显然，\(AB\)比\(CD\)要长。

现在，如果\(x_2\)用毫米\((mm)\)做单位，\(x_1\)保持不变，此时\(A\)坐标\((0, 50)\)，\(C\)坐标为\((0, 100)\)，则

\(d(A, B) = \sqrt{50^2+10^2} = \sqrt {2600}\)
\(d(C, D) = \sqrt{100^2+1^2} = \sqrt {10001}\)

结果\(CD\)反而比\(AB\)长！这显然是不够合理的。

2. 样本分布对距离度量的影响

虽然我们可以先做归一化来消除这种维度间度量单位不同的问题，但是样本分布也会影响距离度量。我们可以看到，欧氏距离中每个坐标的权重是同等的。但是现实问题中，当坐标轴表示观测值时，它们往往带有大小不等的随机波动，即具有不同的方差，显然它们之间的权重是不同的。

下面举两个一维的例子说明这个问题：

设有两个正态分布总体\(G_1: N(\mu_1, \sigma_1^2)\)和\(G_2: N(\mu_2, \sigma_2^2)\)。若有一个样本，其值在点A处，那么，A距离哪个总体近些呢？如图2.2所示：

图2.2

从绝对长度来看，点A距离左面的总体\(G_1\)近些，即点A到\(\mu_1\)比到\(\mu_2\)要近些，（这里用的是欧氏距离，比较的是A点坐标与\(\mu_1\)到\(\mu_2\)值之差的绝对值），但从概率观点来看，A点在\(\mu_1\)右侧约4\(\sigma_1\)处，而在\(\mu_2\)的左侧约3\(\sigma_2\)处，若以标准差来衡量，A点距离\(\mu_2\)要更“近一些”。后者是从概率角度来考虑的，它是用坐标差的平方除以方差（或者说乘以方差的倒数），从而化为无量纲数，推广到多维就要乘以协方差矩阵\(\Sigma\)的逆矩阵\(\Sigma^{-1}\)。

再来看下图2.3，A与B相对于原点的距离是相同的。但是由于样本总体沿着横轴分布，所以B点更有可能是这个样本中的点，而A则更有可能是离群点。在一个方差较小的维度下很小的差别就有可能成为离群点。

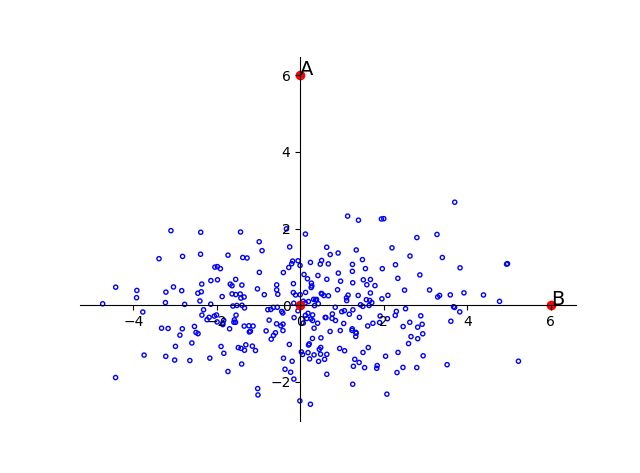
图2.3

3. 维度间具有相关性对距离度量的影响

我们看到，上面描述的情形是维度间或者说特征之间是不相关的，那么如果维度间具有相关性会怎样呢？如下图2.4所示：

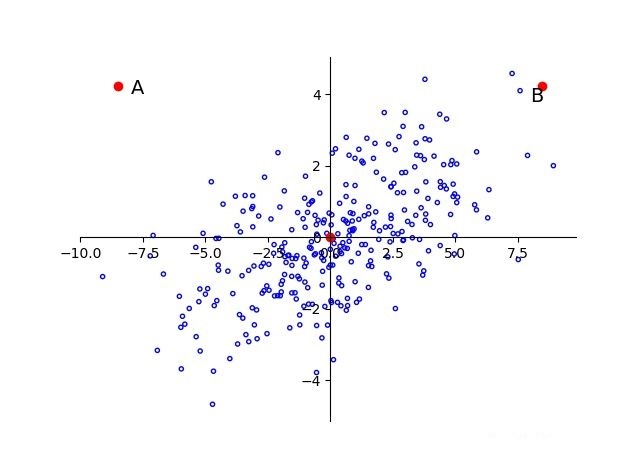
图2.4

可以看到样本点可以近似看做是\(f(x) = x\)的线性分布，A与B相对于原点的距离依旧相等，显然A更像是一个离群点，也即是说离样本总体较远。

即使数据已经经过了标准化，也不会改变AB与原点间距离大小的相互关系。所以要本质上解决这个问题，就要针对主成分分析中的主成分来进行标准化。

为什么标准化不会改变距离大小的相互关系，这里以最常见的z-score标准化(也叫标准差标准化）为例进行简单说明。这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为：\(x^∗=(x−\mu)/\sigma\)，其中\(\mu\)为所有样本数据的均值，\(\sigma\)为所有样本数据的标准差。

显然这里的\(\mu\)和\(\sigma\)都是相同的，所以标准化只相当于对A、B点与数据中心距离进行了一个等比例缩放，并不影响它们之间大小的相互关系。
由此可见，仅仅靠标准化的欧氏距离还是存在很大问题的，数据相关性对判定结果的影响还是很大的。

为什么z-score 标准化后的数据标准差为1?

x-μ只改变均值，标准差不变，所以均值变为0
(x-μ)/σ只会使标准差除以σ倍，所以标准差变为1
即
\(E(x^*) = E[\frac{x-E(x)}{\sqrt{D(x)}}] = \frac{1}{\sqrt{D(x)}}E[x-E(x)]=0\)

\(D(x^*) = D\big[\frac{x-E(x)}{\sqrt{D(x)}}\big] = \frac{1}{D(x)}D[x-E(x)] = \frac{D(x)}{D(x)} = 1\)

OK! 总结一下问题：

  1）要考虑维度间相关性的影响
  2）要考虑方差的影响
  3）要考虑度量单位或者说量纲的影响

因此，有必要建立一种统计距离（只是一种术语，用于区别常用的欧氏距离），这种距离要能够体现各个变量在变差大小上的不同，以及有时存在着的相关性，还要求距离与各变量所用的单位无关。看来我们选择的距离要依赖于样本的方差和协方差。马氏距离就是最常用的一种统计距离。

马氏距离的几何意义

那么怎么办？，其实如果上面内容已经搞懂了，我们就会知道，只需要将变量按照主成分进行旋转，让维度间相互独立，然后进行标准化，让维度同分布就OK了，然后计算马氏距离就变成了计算欧氏距离。

由主成分分析可知，由于主成分就是特征向量方向，每个方向的方差就是对应的特征值，所以只需要按照特征向量的方向旋转，然后缩放特征值倍就可以了，可以得到以下的结果，图2.5：

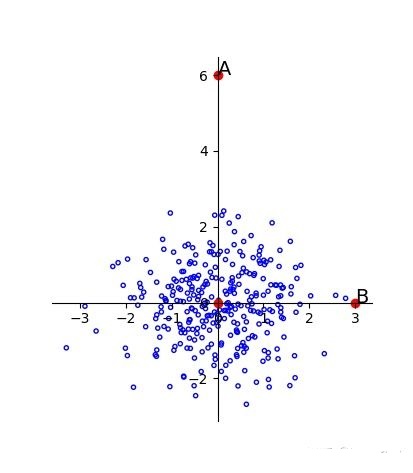
图2.5

离群点就被成功分离，这时候的马氏距离就是欧氏距离。

马氏距离的推导

假设原始的多维样本数据\(X_{n\times m}\)（\(n\)行，\(m\)列）：

\[X_{n\times m} = \begin{matrix} x_{11} & x_{12}& \cdots & x_{1m} \\ x_{21} & x_{22}& \cdots & x_{2m} \\ \vdots & \vdots& \ddots & \vdots \\ x_{n1} & x_{n2}& \cdots & x_{nm} \end{matrix}\]

其中每行表示一个样本，\(X_i\)表示样本的第\(i\)个维度，\(X_i=(x_{1i}, x_{2i}, \dots, x_{ni})^T, i=1, 2, \dots, m\)，则以上多维样本数据可记为：\(X = (X_1, X_2, \dots, X_m)\)

样本总体的均值向量记为：\(\mu_X=(\mu_{X1},\mu_{X2},\dots,\mu_{Xm})\)

协方差矩阵记为：\(\Sigma_X = E[(X-\mu_X)^T(X-\mu_X)] = \frac{1}{n}(X-\mu_X)^T(X-\mu_X)\)

按照之前的描述，首先要对数据进行转换，旋转至主成分，使维度间线性无关。假设将原始数据\(X\)通过坐标旋转矩阵\(U\)变换得到了新的坐标，对应的新数据集记为\(F\)（实际上\(X\)，\(F\)表示的是同一个数据集，只是由于坐标值不同，为了区分而使用不同标记），数据集\(F\)的均值向量记为\(\mu_F=(\mu_{F1},\mu_{F2},\dots,\mu_{Fm})\)，则：

\[F^T = (F_1, F_2, \dots, F_m) = UX^T \]

\[(F-\mu_F)^T = U(X-\mu_X)^T \]

\[(F-\mu_F) = (X-\mu_X)U^T \]

变换后的数据维度间线性无关，且每个维度的方差为特征值，即协方差矩阵\(\Sigma_F\)是对角阵，所以：

\[\begin{aligned} \Sigma_F &= E[(F-\mu_F)^T(F-\mu_F)] \\ &= \frac{1}{n}(F-\mu_F)^T(F-\mu_F) \\ &= \frac{1}{n}U(X-\mu_X)^T(X-\mu_X)U^T \\ &= U\Sigma_XU^T \\ &= \left(\begin{matrix}\lambda_1 & && \\ &\lambda_2&& \\ &&\ddots& \\ &&&\lambda_m\end{matrix}\right) \end{aligned}\]

其中，\(\lambda_i, i=1, 2, \dots, m\)表示每个维度的方差。

推导到这里之后，我们就可以推导出马氏距离公式了，假设要计算\(X\)的一个样本点\(x=(x_1, x_2, \dots, x_3)\)到重心\(\mu_X=(\mu_{X1},\mu_{X2},\dots,\mu_{Xm})\)的马氏距离。等价于求\(F\)中点\(f = (f_1, f_2, \dots, f_m)\)标准化后的坐标值到标准化数据重心坐标值\(\mu_F=(\mu_{F1},\mu_{F2},\dots,\mu_{Fm})\)的欧氏距离。

\[\begin{aligned} d_m^2(f, \mu_F) &= \big(\frac{f_1-\mu_{F1}}{\sqrt{\lambda_1}}\big)^2 + \big(\frac{f_2-\mu_{F2}}{\sqrt{\lambda_2}}\big)^2 + \dots + \big(\frac{f_m-\mu_{Fm}}{\sqrt{\lambda_m}}\big)^2\\ &= (f_1-\mu_{F1},f_2-\mu_{F2},\dots,f_m-\mu_{Fm})\left(\begin{matrix}\frac{1}{\lambda_1} & && \\ &\frac{1}{\lambda_2}&& \\ &&\ddots& \\ &&&\frac{1}{\lambda_m}\end{matrix}\right)\left(\begin{matrix}f_1-\mu_{F1} \\ f_2-\mu_{F2} \\ \vdots\\ f_m-\mu_{Fm}\end{matrix}\right) \\ &= (f-\mu_F)(U\Sigma_XU^T)^{-1}(f-\mu_F)^T \\ &= (x-\mu_X)U^T(U\Sigma_XU^T)^{-1}U(x-\mu_X)^T \\ &= (x-\mu_X)U^T(U^T)^{-1}\Sigma_X^{-1}U^{-1}U(x-\mu_X)^T \\ &= (x-\mu_X)\Sigma_X^{-1}(x-\mu_X)^T \end{aligned}\]

这就是前面定义的马氏距离的计算公式

如果\(x\)是列向量，则

\[d_m^2(f, \mu_F) = (x-\mu_X)^T\Sigma_X^{-1}(x-\mu_X) \]

如果把推导过程中的重心点\(\mu_X\)改换成任意其他样本点\(y\)，则可以得到两个样本点之间的马氏距离公式为：

\[d_m^2(x, y) = (x-y)^T\Sigma_X^{-1}(x-y) \]

假设\(E\)表示一个点集，\(d\)表示距离，它是\(E \times E\)到\([0, \infty)\)的函数，可以证明，马氏距离符合距离度量的基本性质

以上！

 
 
 
机器学习笔记-距离度量与相似度
1）机器学习笔记-距离度量与相似度(一)闵可夫斯基距离
 
 
 
 
 
参考来源：
1）https://www.jianshu.com/p/5706a108a0c6
2）https://blog.csdn.net/u010167269/article/details/51627338
3）https://zhuanlan.zhihu.com/p/46626607
4）多元统计分析-何晓群